Файл: Audio and Radio Engineering.pdf

Propagation 11-37

about 120 ft (36 m) to obtain full first-zone clearance, as shown at “C” in Figure 11.2.9. The cor-
responding clearance for a ridge 100 ft (30 m) in front of either antenna is 4 ft (1.2 m). The locus
of all points that satisfy this condition for all distances is an ellipsoid of revolution with foci at
the two antennas.

When there are two or more knife-edge obstructions or hills between the transmitting and

receiving antennas, an equivalent knife edge can be represented by drawing a line from each
antenna through the top of the peak that blocks the line of sight, as in Figure 11.2.10b.

Note: When accuracy greater
than ±1.5 dB is required, values
on the 

d

1

 scale should be:

1

1

2

2

1

d

d d

+

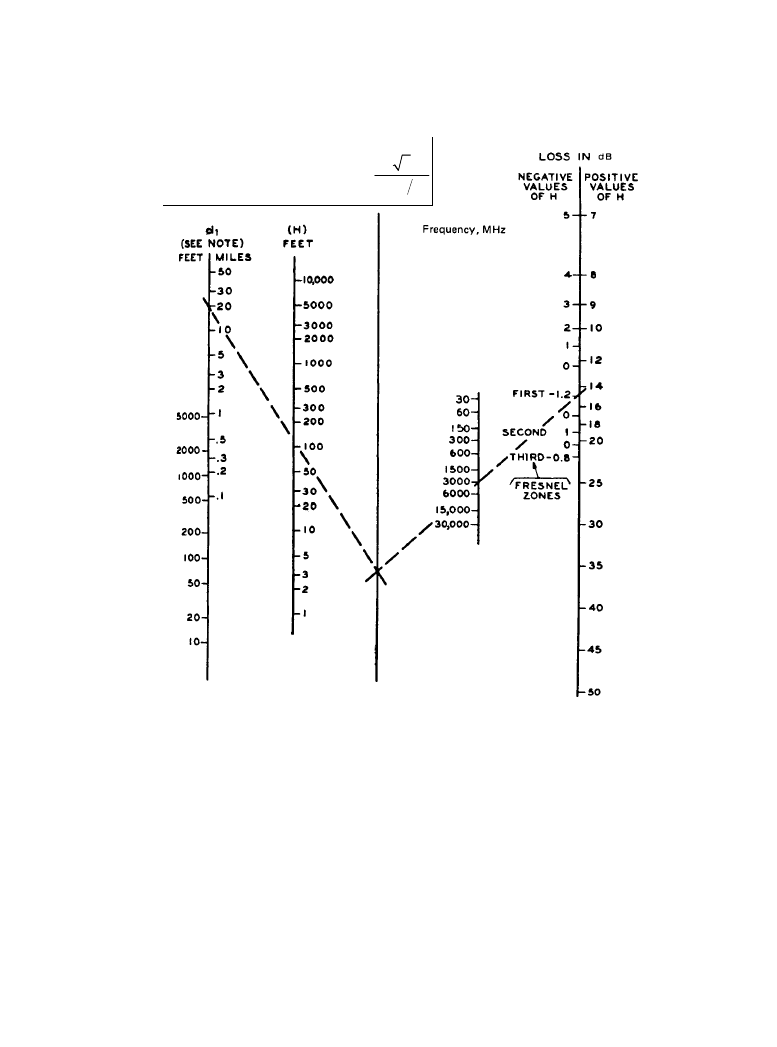
Figure 11.2.11

 Shadow loss relative to free space. (

From [2]. Used with permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Propagation

11-38 Broadcast Transmission Systems

Alternatively, the transmission loss can be computed by adding the losses incurred when

passing over each of the successive hills, as in Figure 11.2.10c. The height H

1

 is measured from

the top of hill 1 to the line connecting antenna 1 and the top of hill 2. Similarly, H

2

 is measured

from the top of hill 2 to the line connecting antenna 2 and the top of hill 1. The nomogram in Fig-
ure 11.2.11 is used for calculating the losses for terrain conditions represented by Figure
11.2.10a–c.

This procedure applies to conditions for which the earth-reflected wave can be neglected,

such as the presence of rough earth, trees, or structures at locations along the profile at points
where earth reflection would otherwise take place at the frequency under consideration; or where
first Fresnel-zone clearance is obtained in the foreground of each antenna and the geometry is
such that reflected components do not contribute to the field within the first Fresnel zone above
the obstruction. If conditions are favorable to earth reflection, the base line of the diffraction tri-
angle should not be drawn through the antennas, but through the points of earth reflection, as in
Figure 11.2.10d. H is measured vertically from this base line to the top of the hill, while d

1

 and

d

2

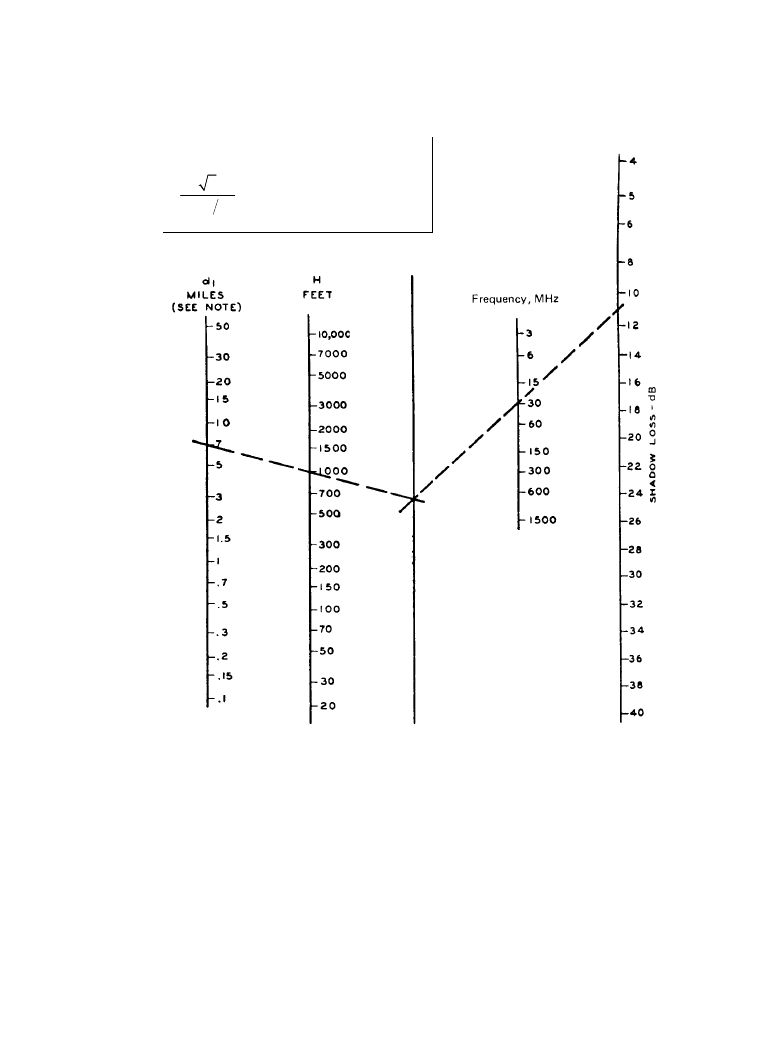
 are measured to the antennas as before. In this case, Figure 11.2.12 is used to estimate the

shadow loss to be added to the plane-earth attenuation [1].

Under conditions where the earth-reflected components reinforce the direct components at

the transmitting and receiving antenna locations, paths may be found for which the transmission
loss over an obstacle is less than the loss over spherical earth. This effect may be useful in estab-
lishing VHF relay circuits where line-of-sight operation is not practical. Little utility, however,
can be expected for mobile or broadcast services [14].

An alternative method for predicting the median value for all measurements in a completely

shadowed area is as follows [15]:

1.

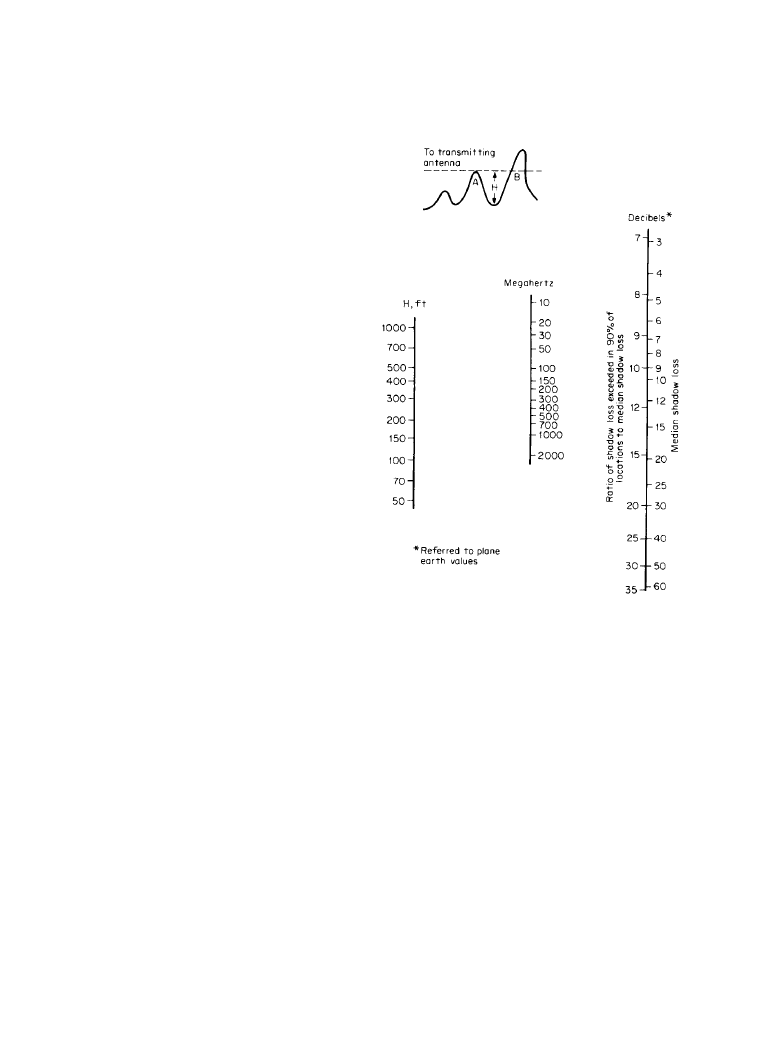
The roughness of the terrain is assumed to be represented by height H, shown on the profile
at the top of Figure 11.2.13.

2.

This height is the difference in elevation between the bottom of the valley and the elevation
necessary to obtain line of sight with the transmitting antenna.

3.

The difference between the measured value of field intensity and the value to be expected
over plane earth is computed for each point of measurement within the shadowed area. 

4.

The median value for each of several such locations is plotted as a function of sq. rt. (H/

λ).

These empirical relationships are summarized in the nomogram shown in Figure 11.2.13. The
scales on the right-hand line indicate the median value of shadow loss, compared with plane-
earth values, and the difference in shadow loss to be expected between the median and the 90
percent values. For example, with variations in terrain of 500 ft (150 m), the estimated median
shadow loss at 4500 MHz is about 20 dB and the shadow loss exceeded in 90 percent of the pos-
sible locations is about 20 + 15 = 35 dB. This analysis is based on large-scale variations in field
intensity, and does not include the standing-wave effects that sometimes cause the field intensity
to vary considerably within a matter of a few feet.

Effects of Buildings

Built-up areas have little effect on radio transmission at frequencies below a few megahertz,
since the size of any obstruction is usually small compared with the wavelength, and the shadows
caused by steel buildings and bridges are not noticeable except immediately behind these
obstructions. However, at 30 MHz and above, the absorption of a radio wave in going through an

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Propagation

Propagation 11-39

obstruction and the shadow loss in going over it are not negligible, and both types of losses tend
to increase as the frequency increases. The attenuation through a brick wall, for example, can
vary from 2 to 5 dB at 30 MHz and from 10 to 40 dB at 3000 MHz, depending on whether the
wall is dry or wet. Consequently, most buildings are rather opaque at frequencies of the order of
thousands of megahertz.

For radio-relay purposes, it is the usual practice to select clear sites; but where this is not fea-

sible the expected fields behind large buildings can be predicted by the preceding diffraction

Figure 11.2.12

 Shadow loss relative to plane earth. (

From [2]. Used with permission.)

1

1

2

2

1

d

d d

+

Note: When accuracy greater than ±1.5 dB is
required, values on the 

d

1

 scale should be:

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Propagation

11-40 Broadcast Transmission Systems

methods. In the engineering of mobile- and broadcast-radio systems it has not been found practi-
cal in general to relate measurements made in built-up areas to the particular geometry of build-
ings, so that it is conventional to treat them statistically. However, measurements have been
divided according to general categories into which buildings can readily be classified, namely,
the tall buildings typical of the centers of cities on the one hand, and typical two-story residential
areas on the other.

Buildings are more transparent to radio waves than the solid earth, and there is ordinarily

much more backscatter in the city than in the open country. Both of these factors tend to reduce
the shadow losses caused by the buildings. On the other hand, the angles of diffraction over or
around the buildings are usually greater than for natural terrain, and this factor tends to increase
the loss resulting from the presence of buildings. Quantitative data on the effects of buildings
indicate that in the range of 40 to 450 MHz there is no significant change with frequency, or at
least the variation with frequency is somewhat less than the square-root relationship noted in the
case of hills. The median field strength at street level for random locations in New York City is
about 25 dB below the corresponding plane-earth value. The corresponding values for the 10
percent and 90 percent points are about –15 and –35 dB, respectively [1, 15]. Measurements in
congested residential areas indicate somewhat less attenuation than among large buildings.

Figure 11.2.13

 Estimated distribu-

tion of shadow loss for random
locations (referred to plane-earth
values). (

From [2]. Used with per-

mission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Propagation

Propagation 11-41

Effects of Trees and Other Vegetation

When an antenna is surrounded by moderately thick trees and below treetop level, the average
loss at 30 MHz resulting from the trees is usually 2 or 3 dB for vertical polarization and negligi-
ble with horizontal polarization. However, large and rapid variations in the received field
strength can exist within a small area, resulting from the standing-wave pattern set up by reflec-
tions from trees located at a distance of as much as 100 ft (30 m) or more from the antenna. Con-
sequently, several nearby locations should be investigated for best results. At 100 MHz, the
average loss from surrounding trees may be 5 to 10 dB for vertical polarization and 2 or 3 dB for
horizontal polarization. The tree losses continue to increase as the frequency increases, and
above 300 to 500 MHz they tend to be independent of the type of polarization. Above 1000
MHz, trees that are thick enough to block vision present an almost solid obstruction, and the dif-
fraction loss over or around these obstructions can be obtained from Figures 11.2.9 or 11.2.11.

There is a pronounced seasonal effect in the case of deciduous trees, with less shadowing and

absorption in the winter months when the leaves have fallen. However, when the path of travel
through the trees is sufficiently long that it is obscured, losses of the above magnitudes can be
incurred, and the principal mode of propagation may be by diffraction over the trees.

When the antenna is raised above trees and other forms of vegetation, the prediction of field

strengths again depends upon the proper estimation of the height of the antenna above the areas
of reflection and of the applicable reflection coefficients. For growth of fairly uniform height and
for angles near grazing incidence, reflection coefficients will approach –1 at frequencies near 30
MHz. As indicated by Rayleigh’s criterion of roughness, the apparent roughness for given condi-
tions of geometry increases with frequency so that near 1000 MHz even such low and relatively
uniform growth as farm crops or tall grass may have reflection coefficients of about –0.3 for
small angles of reflection [17].

The distribution of losses in the immediate vicinity of trees does not follow normal probabil-

ity law but is more accurately represented by Rayleigh’s law, which is the distribution of the sum
of a large number of equal vectors having random phases.

11.2.3f

Effects of the Lower Atmosphere (Troposphere)

Radio waves propagating through the lower atmosphere, or troposphere, are subject to absorp-
tion, scattering, and bending. Absorption is negligible in the VHF–UHF frequency range but
becomes significant at frequencies above 10 GHz. The index of refraction of the atmosphere, n,
is slightly greater than 1 and varies with temperature, pressure, and water vapor pressure, and
therefore with height, climate, and local meteorological conditions. An exponential model show-
ing a decrease with height to 37 to 43 mi (60 to 70 kin) is generally accepted [18, 19]. For this
model, variation of n is approximately linear for the first kilometer above the surface in which
most of the effect on radio waves traveling horizontally occurs. For average conditions, the effect
of the atmosphere can be included in the expression of earth diffraction around the smooth earth
without discarding the useful concept of straight-line propagation by multiplying the actual
earth’s radius by k to obtain an effective earth’s radius, where

(11.2.24)

(

)

1

1

k

a dn dh

=

+

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Propagation