Файл: Audio and Radio Engineering.pdf

11-32 Broadcast Transmission Systems

attenuation and bending of the ray. Thus, all shadows are somewhat “fuzzy” on the edges and the
transition from “light” to “dark” areas is gradual, rather than infinitely sharp.

The effect of diffraction around the earth’s curvature is to make possible transmission beyond

the line of sight, with somewhat greater loss than is incurred in free space or over plane earth.
The magnitude of this loss increases as either the distance or the frequency is increased and it
depends to some extent on the antenna height.

The calculation of the field strength to be expected at any particular point in space beyond the

line of sight around a spherical earth is rather complex, so that individual calculations are seldom
made except with specially designed software. Rather, nomograms or families of curves are usu-
ally prepared for general application to large numbers of cases. The original wave equations of
Van der Pol and Bremmer [6] have been modified by Burrows [7] and by Norton [3, 5] so as to
make them more readily usable and particularly adaptable to the production of families of
curves. Such curves have been prepared by a variety of organizations. These curves have not
been included herein, in view of the large number of curves that are required to satisfy the possi-
ble variations in frequency, electrical characteristics of the earth, polarization, and antenna
height. Also, the values of field strength indicated by smooth-earth curves are subject to consid-
erable modification under actual conditions found in practice. For VHF and UHF broadcast pur-
poses, the smooth-earth curves have been to a great extent superseded by curves modified to
reflect average conditions of terrain.

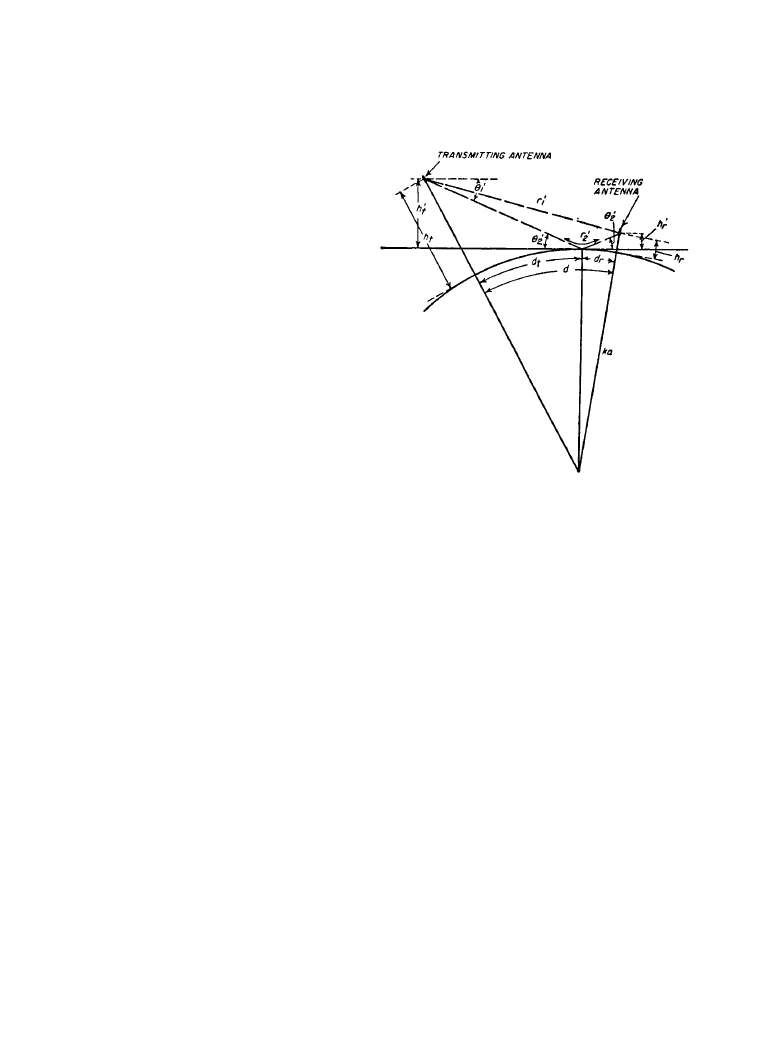
Figure 11.2.7 is a nomogram to determine the additional loss caused by the curvature of the

earth [1]. This loss must be added to the free-space loss found from Figure 11.2.1. A scale is
included to provide for the effect of changes in the effective radius of the earth, caused by atmo-
spheric refraction. Figure 11.2.7 gives the loss relative to free space as a function of three dis-
tances; d

1

 is the distance to the horizon from the lower antenna, d

2

 is the distance to the horizon

Figure 11.2.6

 Ray paths for

antennas above spherical earth.
(

From [2]. Used with permis-

sion.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Propagation

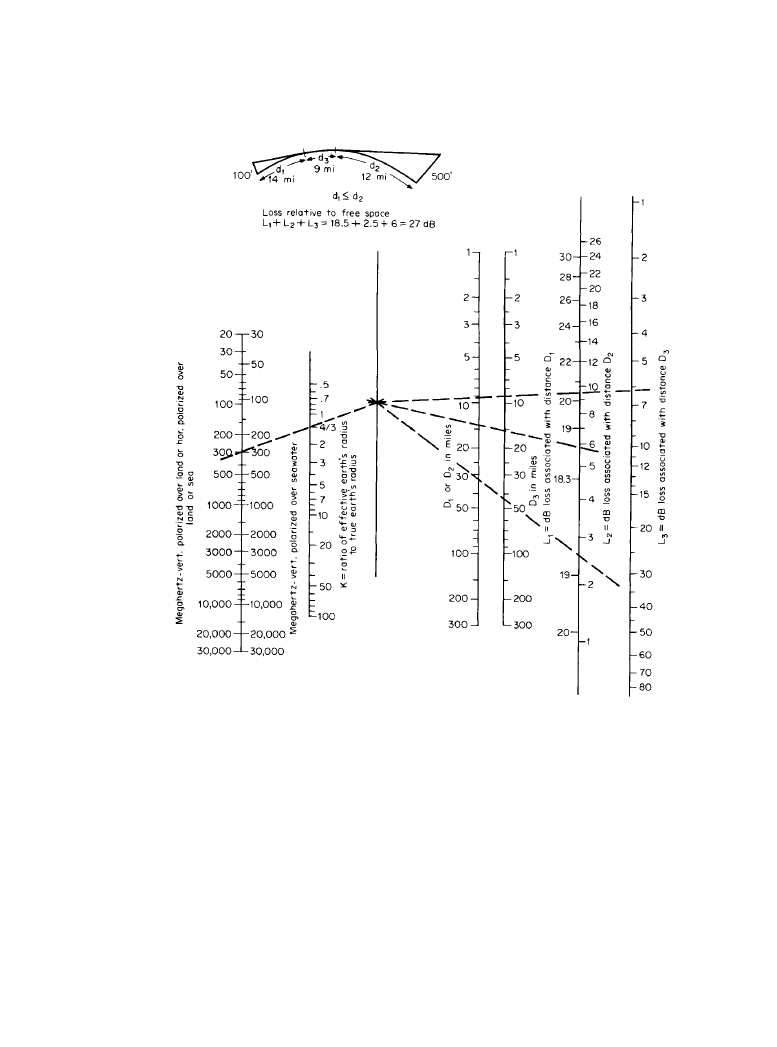
Propagation 11-33

from the higher antenna, and d

3

 is the distance between the horizons. The total distance between

antennas is d = d

1

 + d

2

 + d

3

.

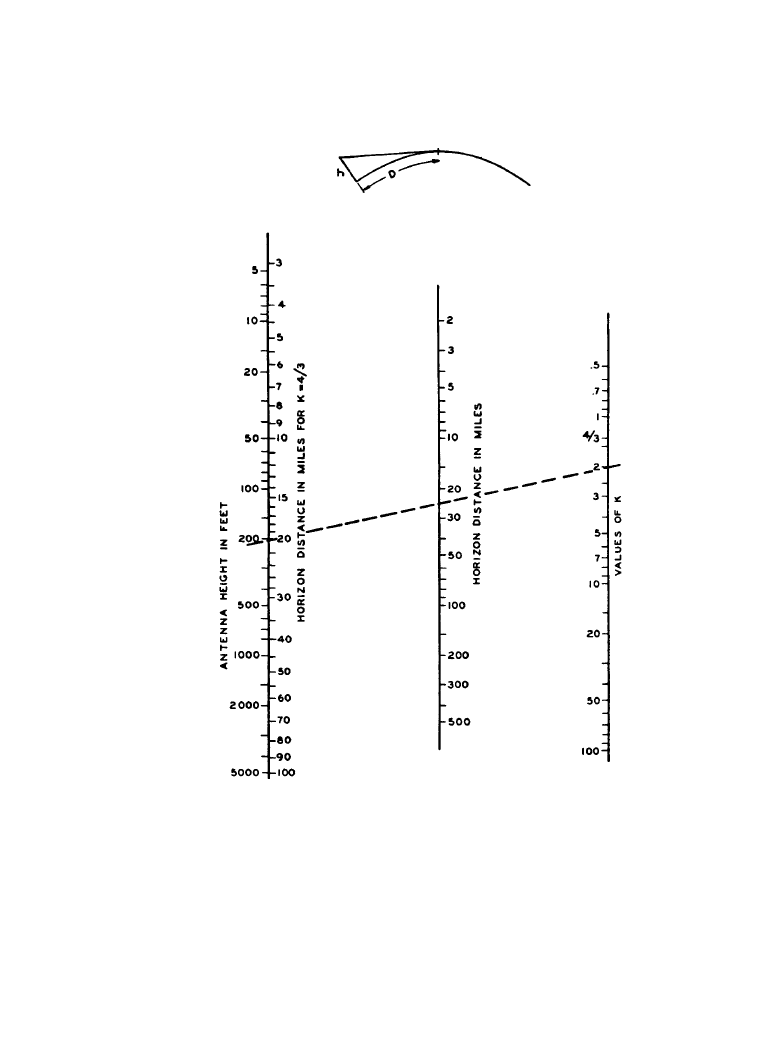
The horizon distances d

1

 and d

2

 for the respective antenna heights h

1

 and h

2

 and for any

assumed value of the earth’s radius factor k can be determined from Figure 11.2.8 [1].

Figure 11.2.7 

Loss beyond line of sight in decibels. (

From [2]. Used with permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Propagation

11-34 Broadcast Transmission Systems

11.2.3e

Effects of Hills, Buildings, Vegetation, and the Atmosphere

The preceding discussion assumes that the earth is a perfectly smooth sphere with a uniform or a
simple atmosphere, for which condition calculations of expected field strengths or transmission

Figure 11.2.8

 Distance to the horizon. (

From [2]. Used with permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Propagation

Propagation 11-35

losses can be computed for the regions within the line of sight and regions well beyond the line
of sight, and interpolations can be made for intermediate distances. The presence of hills, build-
ings, and trees has such complex effects on propagation that it is impossible to compute in detail
the field strengths to be expected at discrete points in the immediate vicinity of such obstructions
or even the median values over very small areas. However, by the examination of the earth pro-
file over the path of propagation and by the use of certain simplifying assumptions, predictions
that are more accurate than smooth-earth calculations can be made of the median values to be
expected over areas representative of the gross features of terrain.

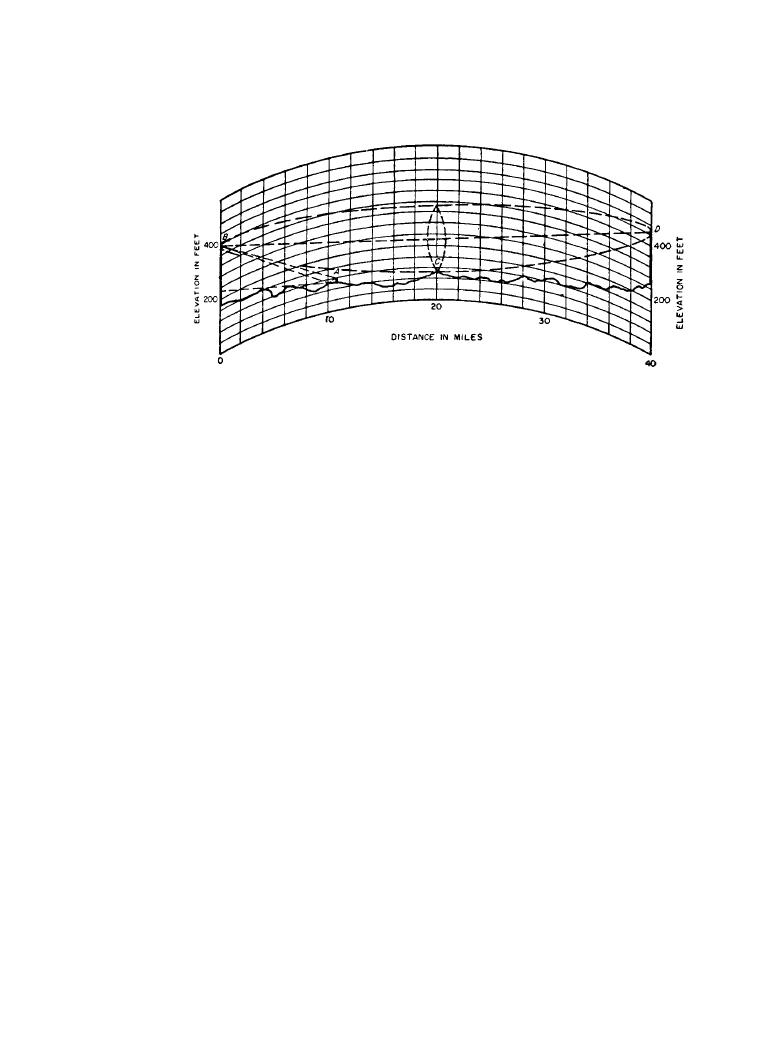
Effects of Hills

The profile of the earth between the transmitting and receiving points is taken from available
topographic maps and is plotted on a chart that provides for average air refraction by the use of a
4/3 earth radius, as shown in Figure 11.2.9. The vertical scale is greatly exaggerated for conve-
nience in displaying significant angles and path differences. Under these conditions, vertical
dimensions are measured along vertical parallel lines rather than along radii normal to the curved
surface, and the propagation paths appear as straight lines. The field to be expected at a low
receiving antenna at A from a high transmitting antenna at B can be predicted by plane-earth
methods, by drawing a tangent to the profile at the point at which reflection appears to occur
with equal incident and reflection angles. The heights of the transmitting and receiving antennas
above the tangent are used in conjunction with Figure 14.4.5 to compute the transmission loss, or
with Equation (11.2.21) to compute the field strength. A similar procedure can be used for more
distantly spaced high antennas when the line of sight does not clear the profile by at least the first
Fresnel zone [10].

Propagation over a sharp ridge, or over a hill when both the transmitting and receiving

antenna locations are distant from the hill, may be treated as diffraction over a knife edge, shown
schematically in Figure 11.2.10a [1, 9–14]. The height of the obstruction H is measured from the
line joining the centers of the two antennas to the top of the ridge. As shown in Figure 11.2.11,

Figure 11.2.9

 Ray paths for antennas over rough terrain. (

From [2]. Used with permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Propagation

11-36 Broadcast Transmission Systems

the shadow loss approaches 6 dB as H approaches 0—grazing incidence—and it increases with
increasing positive values of H. When the direct ray clears the obstruction, H is negative, and the
shadow loss approaches 0 dB in an oscillatory manner as the clearance is increased. Thus, a sub-
stantial clearance is required over line-of-sight paths in order to obtain free-space transmission.
There is an optimum clearance, called the first Fresnel-zone clearance, for which the transmis-
sion is theoretically 1.2 dB better than in free space. Physically, this clearance is of such magni-
tude that the phase shift along a line from the antenna to the top of the obstruction and from there
to the second antenna is about one-half wavelength greater than the phase shift of the direct path
between antennas.

The locations of the first three Fresnel zones are indicated on the right-hand scale on Figure

11.2.11, and by means of this chart the required clearances can be obtained. At 3000 MHz, for
example, the direct ray should clear all obstructions in the center of a 40 mi (64 km) path by

(

a)

(

b)

(

c)

(

d)

Figure 11.2.10

 Ray paths for antennas behind hills: (

a–d), see text. (From [2]. Used with permis-

sion.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Propagation