Файл: Audio and Radio Engineering.pdf

2-22 The Audio Spectrum

In the example f(t) = cos (

ωt), the amplitude and instantaneous frequency of the associated

analytic signal are 1 and 

ω, respectively.

While the analytic signal is a linear transformation of the signal that, in effect, converts nega-

tive-frequency components in the spectrum of f(t) to positive-frequency components, the enve-
lope  E(t) and instantaneous frequency 

ω

i

(t) are nonlinear functions of f(t) and 

. For more

complicated signals, 

ω

i

(t) is, in general, not the same as 

ω in the spectrum.

The spectral operation of advancing the phases of all positive-frequency components by 90°

and advancing the phases of all negative-frequency components by 90° is called Hilbert transfor-
mation; that is, 

 is the Hilbert transform of f(t).

2.1.3

Bibliography

Bracewell, R.: The Fourier Integral and Its Applications, McGraw-Hill, New York, N.Y., 1965.

Childers, D. G.: Modern Spectral Analysis, IEEE, New York, N.Y., 1978.

Connor, F. R.: Signals, Arnold, London, 1972.

Jenkins, G. M., and D. G. Watts: Spectral Analysis and Its Applications, Holden-Day, San Fran-

cisco, Calif., 1968.

fˆ t

( )

fˆ t

( )

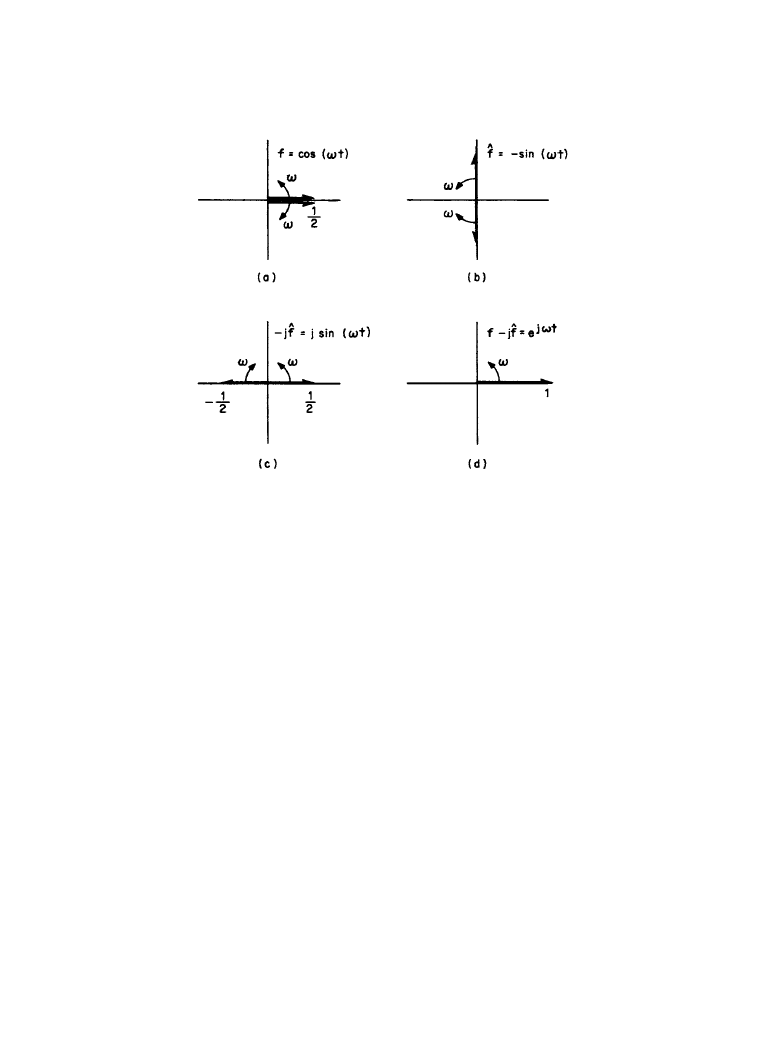
Figure 2.1.6 

Formation of analytic signal 

 of 

: (

a) counterrotating phasors represent-

ing ; 

(

b)  , the Hilbert transform of  ; (c) –  times each phasor in b; (d) analytic sig-

nals given by sum of phasors in 

a and c.

e

j

ωt

ωt

( )

cos

f

ωt

( )

cos

=

fˆ

f

j

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Signals and Spectra

Signals and Spectra 2-23

Kharkevich, A. A.: Spectra and Analysis, English translation, Consultants Bureau, New York,

N.Y., 1960.

Lynn, P. A.: An Introduction to the Analysis and Processing of Signals, 2nd ed. Macmillan, Lon-

don, 1982.

Panter, P. F.: Modulation, Noise and Spectral Analysis, McGraw-Hill, New York, N.Y., 1965.

Papoulis, A.: The Fourier Integral and Its Applications, McGraw-Hill, New York, N.Y., 1962.

Rabiner, L. R., and C. M. Rader (eds.): Digital Signal Processing, IEEE, New York, N.Y., 1972.

Schwartz, M.: Information Transmission, Modulation and Noise, McGraw-Hill, New York, N.Y.,

1970.

Westman, H. P. (ed.): ITT Reference Data for Radio Engineers, Howard W. Sams, New York,

N.Y., 1973.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Signals and Spectra

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Signals and Spectra

2-25

Chapter

2.2

Spectral Changes and Linear Distortion

Douglas Preis

2.2.1

Introduction

When a reproduced signal is not a replica of the original signal, it is distorted.  Distortionless
transmission of a time-varying signal through a system requires that the signal's shape be pre-
served. The two general mechanisms of signal distortion are nonlinear and linear.

2.2.2

Distortion Mechanisms

In a broad context, nonlinear distortion includes all forms of output-signal corruption that are
not linearly related to (i.e., statistically linearly dependent on or correlated with) the input signal.
Modulation (amplitude or frequency) of the signal (or even its time derivatives) by an imperfect
system produces a certain amount of up conversion and down conversion of the signal's fre-
quency components. For example, squaring or cubing of the signal resulting from a nonlinear
transfer characteristic is a form of (self) amplitude modulation, whereas time-base errors, like
speed variations, are equivalent to frequency modulation of the signal. These converted frequen-
cies, like noise, are not linearly related to the input. The coherence function 

is a quantita-

tive measure of the cumulative effect, at each frequency, of these various forms of signal
corruption.

Linear distortion implies that even though the output signal is linearly related to the input, the

shape of the output signal is different from that of the input signal. The system itself is linear and
does process signals linearly (i.e., scale factors are preserved, and superposition is valid), but lin-
ear mathematical operations on the input signal such as differentiation or integration are permis-
sible. Linear distortion changes the relative relationships among the existing constituents of the
signal by altering either intensity or timing, or both, of its different frequency components. As a
consequence, the output signal has a different shape. The system function (or complex frequency
response) only predicts the spectral changes that the spectrum of the input signal will undergo
and not the change of signal shape in time. The actual time-domain signal must be computed
from direct convolution or inverse Fourier transformation.

When a single sinusoid is used as an input to a linear system, the corresponding steady-state

output is also a sinusoid of the same frequency but, generally, with different amplitude and phase
as prescribed by the complex frequency response. This single sinusoid is never linearly distorted

γ

2

ω

( )

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Source: Standard Handbook of Audio and Radio Engineering

2-26 The Audio Spectrum

because it always is a replica of the input. In contrast, if the frequency content of the input signal
is discrete (e.g., a square wave) or continuous (e.g., a single rectangular pulse), then linear distor-
tion is observable as waveshape change. The extent to which an input signal will be linearly dis-
torted depends on both its spectrum and the system function or complex frequency response of
the linear system that processes it. Linear distortion encompasses what is sometimes called tran-
sient distortion, meaning the waveshape change of a finite-energy (transient) input signal (e.g., a
short tone burst or pulse) under linear operating conditions. Finite-power input signals such as
square waves, random noise, music, or speech also can be linearly distorted, however. Nonlinear
effects such as clipping or slew-rate limiting of transient signals are a form of nonlinear distor-
tion, which implies that transient distortion can be amibiguous terminology.

2.2.2a

Linear Range

The range of linear operation of a system is usually established with sine-wave signals. The most
frequently used procedure is to verify, using a single sine-wave input, whether the magnitude-
scale factor is preserved as input amplitude is changed and/or to verify, using two sinusoids of
different frequency simultaneously as an input, whether superposition is valid. Both procedures
examine the linearity hypothesis under sinusoidal, steady-state operating conditions. Because the
input spectrum is as narrow as possible (a line spectrum consisting of one or two discrete fre-
quencies), the spectrum of the output can easily reveal the existence of other, or “new,” frequen-
cies which would constitute nonlinear distortion corresponding to the chosen input signal. The
ratio of total power contained in these other frequencies to the output power at the input fre-
quency (or frequencies), expressed in percentage or decibels, is often used as both a measure and
a specification of nonlinear distortion (e.g., harmonic distortion, intermodulation distortion, or
dynamic intermodulation distortion, depending on the specific choice of input frequencies). This
method of testing linearity is relatively simple and can be very sensitive. With modern, wide-
dynamic-range, high-resolution spectrum analyzers and high-purity sine-wave generators, the
effects of very small amounts of nonlinearity can be measured for sinusoidal steady-state opera-
tion.

Some aspects of this kind of spectral analysis are questionable, however. Incoherent (uncorre-

lated) power can exist at the test frequency itself (e.g., due to cubic nonlinearity, time-base
errors, or noise), and, even more important, the system is never excited throughout its full operat-
ing bandwidth by the test signal. Because nonlinear effects do not superpose, the percentage of
sine-wave nonlinear distortion measured, for example, as a function of test-signal frequency for
fixed-output-power level, is not the same as the percentage of uncorrelated output power as a
function of frequency for broadband operation with nonsinusoidal input signals. The latter can
be expressed by using the coherence function to define a frequency-dependent signal-to-noise
ratio as the ratio of coherent power to incoherent power, expressed in percentage or decibels.

2.2.2b

Spectra Comparison

Comparison of input and output spectra of a system is worthwhile. Spectral changes can indicate,
in the frequency domain, the existence of linear distortion as well as nonlinear distortion. For lin-
ear operation, the spectral changes that any input signal undergoes are predicted by the system
function or complex frequency response. For nonlinear operation, the portion of the output sig-

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Spectral Changes and Linear Distortion