Файл: Audio and Radio Engineering.pdf

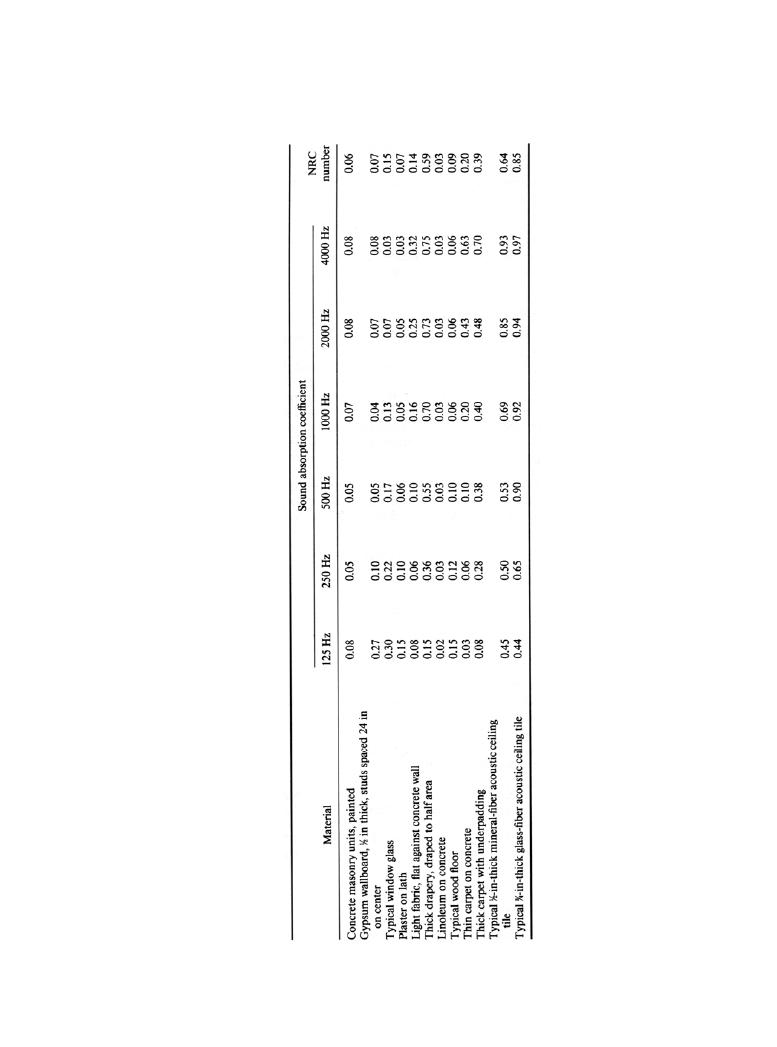
3-10 Architectural Acoustic Principles and Design Techniques

T

a

b

le 3.

1.

2 T

y

p

ic

a

l 

A

b

so

rp

ti

o

n

 C

o

e

ff

ic

ie

n

ts

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

The Physical Nature of Sound

The Physical Nature of Sound 3-11

3.1.3a

Frictional Absorbers

Most of the commonly available materials intended for the absorption of sound, such as acoustic
ceiling tile and acoustic foam, are frictional absorbers. They are porous materials that allow for
the passage of air and, as a result, the passage of sound waves through them. The sound waves
cause molecular motion within the narrow restrictions in the material which results in friction,
converting a fraction of the sound energy to heat.

As an acoustical panel is increased in thickness or moved away from a solid backing surface,

its absorption at low frequency improves. The application of a facing reduces the effect of high-
frequency absorption; common facings are plastic membranes, wood slats, and woven fabric.
Material manufacturers provide the absorption coefficient for various frequencies and for differ-
ent styles of mounting.

Frictional absorbers by themselves are not very useful for reducing sound as it is transmitted

from one side of the material to the other. Materials with a good transmission loss are used for
this purpose.

3.1.3b

Resonant Panels

Sound energy may also be reduced when reflected from impervious resonant panels, such as
those made from gypsum board or plywood. Incident sound on the panel causes it to vibrate, the
air and the material behind the panel dampen the movement, some of the sound is converted to
heat, and the remainder is reradiated. For these panels to be effective, they must be large com-
pared with the wavelength of the sound, be fully baffled at the sides and rear, and be tuned to the
desired resonant frequency. The maximum absorption coefficient of such a panel is typically 0.5
over a frequency range of an octave. They are most usefully applied at resonant frequencies
below 300 Hz. They are usually custom-designed for specific applications.

A typical absorber may be a 4- by 8-ft sheet of plywood 1/2 in thick held a distance d away

from a solid wall by means of studs around its periphery. It is sealed to the wall and studs, and
the cavity is lightly filled with sound-absorptive material. The resonance frequency is given by

(3.1.4)

where:
K = 174 (K = 60)
m = surface weight, lb/ft (kg/m)
d = panel spacing from wall, in (m)

For this example, the plywood weighs 2 lb/ft and d = 1.5 in; then

(3.1.4a)

The maximum number of sabins that this typical panel can provide at this frequency can be

calculated by multiplying its area by the absorption coefficient

(3.1.4b)

f

r

K/ md

=

f

r

174

=

/ 2

1.5

×

100Hz

=

A

4

8

0.5

×

×

16

=

=

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

The Physical Nature of Sound

3-12 Architectural Acoustic Principles and Design Techniques

In this calculation, Equation (3.1.4) is a simplified version of a much more complex equation,

and its application is limited to large flexible panels that have a low resonant frequency.

In some situations, construction using such materials as gypsum wallboard for a partition that

is intended to be reflective may inadvertently be absorptive in one or two octave bands because
of panel resonance. Two walls, perhaps on opposite sides of a studio, may appear identical, but if
one is a freestanding partition and the other is mounted to a masonry wall, their absorption coef-
ficients may be significantly different.

3.1.3c

Cavity Resonators

The most popular form of cavity resonator is a cinder block manufactured with a slot formed
through to its internal cavity. This is also most effective at lower frequencies, but it has an
absorption coefficient close to 1 at the resonant frequency. The volume of the cavity and the
dimensions of the slot determine this frequency. When the cavity of the block is stuffed with
fiberglass, the range of frequencies over which the block is effective is increased from one or two
octaves to two or three. When these blocks are assembled into large walls, the total number of
sabins is obtained by multiplying the manufacturer's absorption coefficient by the wall area [see
Equation (3.1.3)].

3.1.3d

Reverberation

After the generation of sound within an enclosed space has ceased, the sound wave continues to
travel, striking surfaces until it is entirely absorbed. The time taken for the sound pressure level
to decay by 60 dB from its original level is called the reverberation time. There are two basic
controlling factors: room volume and total sound absorption. The reverberation time T, in sec-
onds is given by

(3.1.5a)

Where:
V = volume of room, ft

3

A = total area of absorption, sabins

or in metric sabins

(3.1.5b)

where V = volume of room, m

3

.

Equation (3.1.5) assumes that the sound pressure level is equally diffused throughout the

room. In many actual situations, full diffusion does not exist because of large single areas of
absorption. For example, the audience may provide most of the absorption in an auditorium, or a
studio may be designed with a dead end. In some cases, two reverberation times may be exhib-
ited simultaneously. The decay of sound may have an envelope of two line segments, one for
each reverberation time, with the second segment being apparent only after the decay of the first.
Thus, caution should be exercised when using a digital reverberation-time meter, for it may
obscure valuable information or give erroneous data.

T

60

0.05V/A

=

T

60

0.161V/A

=

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

The Physical Nature of Sound

The Physical Nature of Sound 3-13

Equation (3.1.5) can be expressed in an alternative way to show the result of adding to a room

volume or adding acoustically absorptive material to the material already in place. From Equa-
tion (3.1.5)

Change in T

60

 (%) = (change in % of volume) – (change in % total absorption)

(3.1.6)

Thus, if the reverberation time of a space needs to be decreased, the percentage addition of

absorptive material has to be significant. This can be understood intuitively from experience in
which opening a door in a typical room that may have 200 sabins, and thus creating a totally
absorptive area of an additional 20 ft

2

 does not noticeably change the reverberation time. From

Equation (3.1.6) the change in T

60

is only 10 percent.

3.1.3e

Combination of Direct and Reverberant Sound

The sound level within a space consists of two parts: 1) the sound that comes directly from the
source and 2) the reverberant sound. Very close to the source the direct sound predominates. Fur-
ther away, the direct sound decreases by 6 dB at each doubling of the distance while the reverber-
ant-sound level stays almost constant. At a distant point, the direct sound contributes
insignificantly to the total sound level, and no matter how much more distance from the source is
increased, the sound level remains constant at the reverberant level.

At an intermediate point, at a distance from the source known as the critical distance, the

direct sound is equal to the reverberant sound. This distance depends on the total absorption [see
Equation (3.1.3) for total number of sabins] within the space and the directivity of the source.

If it is proposed to reduce sound within a space by means of absorption, applying an infinite

amount will remove only the reverberant-sound contribution, not the direct sound. Of course,
because of space constraints only limited amounts of absorption can be applied, with the result
that not all the reverberant sound can be removed.

The critical distance is the closest distance at which any discernible sound-level reduction (3

dB) can be obtained by the application of absorptive materials. In addition, when taking into
account the fact that a 3-dB reduction is just discernible but may not be significant, the cost of
absorptive materials for noise reduction at the critical distance may not be justified. Noise con-
trol by means of absorption is usually practical only beyond 2 to 3 times the critical distance.

To calculate the critical distance, first calculate the room constant R

(3.1.7a)

The critical distance d is

(3.7b)

The result of this calculation gives an immediate perspective on whether to control the sound

through absorption within the space or to apply alternative means.

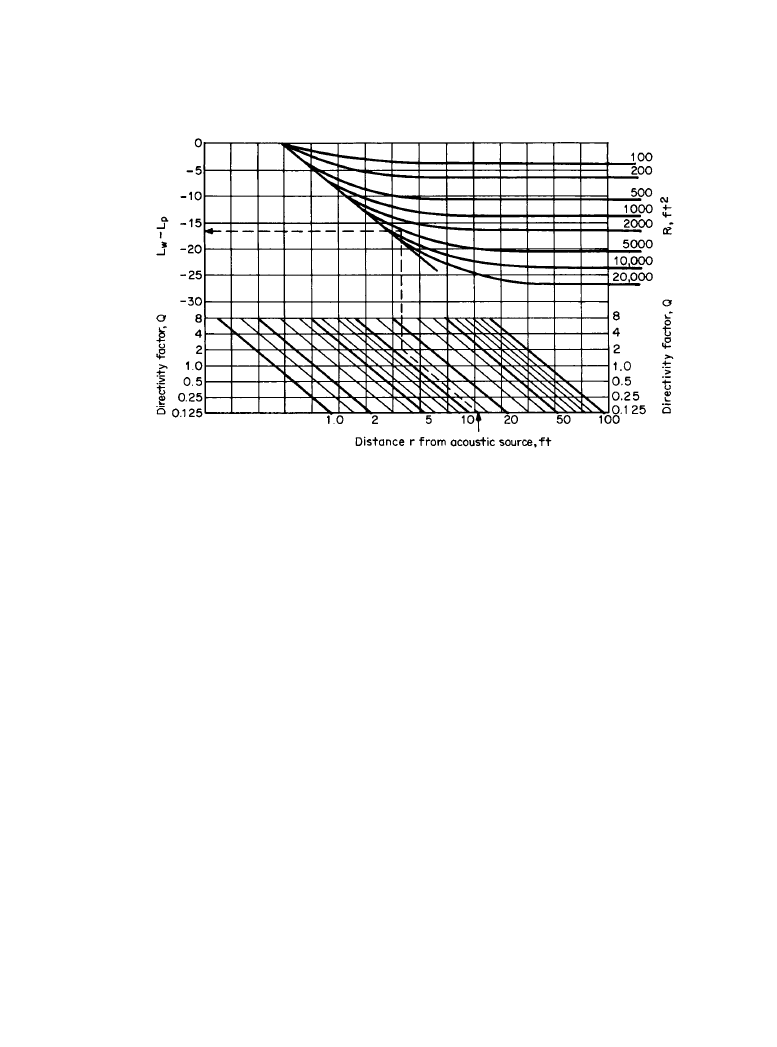
The parameters here are interrelated, as shown in Figure 3.1.2. The upper half of the figure

shows a diagonal line indicating the direct sound falling at 6 dB of each doubling of distance.

R

A

ΣS

ΣS A

–

----------------

=

d

RQ/16

π

=

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

The Physical Nature of Sound

3-14 Architectural Acoustic Principles and Design Techniques

The asymptotic lines show the contribution of reverberant sound. The lower half of the figure
applies to source directivity. For example, at a distance r, 12 ft from a source with a directivity
factor Q of 2, in a room with a room constant R of 5000 ft

2

, the sound pressure level will be 17

dB less than the sound power level. Note that r also is approximately the critical distance where
the sound level is 3 dB above the direct level.

Though the sound level within a space can be controlled to a limited degree through the appli-

cation of absorptive materials, building a partition can be much more effective in separating a
noise source from a listener, although it can never totally prevent all the sound from passing
through.

Actually, sound does not pass “through” a typical wall. The sound pressure on one side of the

wall results in a force that shakes the wall. The shaking wall in turn disturbs the air on the other
side, causing sound pressure waves to spread again and thus to establish a new sound level in the
receiving space.

The difference between the levels on either side of the wall is called the noise reduction of the

wall. The noise reduction (NR) depends not only on the characteristics of the wall but on the total
absorption in the receiving space. For example, a wall enclosing a highly reverberant room is sig-
nificantly less effective than the same wall protecting a well-upholstered lounge. Thus, to help in
defining the acoustical performance of the wall alone, a measure that is independent of the
acoustical characteristics of the receiving space is required. This is termed transmission loss
(TL).

In one typical situation, in which the sound travels from one reverberant space to another, the

transmission loss of the wall is related to noise reduction by

Figure 3.1.2

 Relationship between distance from source, directivity factor, room constant, and 

L

w

–

L

p

.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

The Physical Nature of Sound