ВУЗ: Казахская Национальная Академия Искусств им. Т. Жургенова
Категория: Книга
Дисциплина: Не указана
Добавлен: 03.02.2019
Просмотров: 21685
Скачиваний: 19

6-16 Digital Coding of Audio Signals
(6.2.1)
Where:
y[n] = output of the filter at integer sample index n
x[n] = input to the filter at integer sample index n
b
k
= filter weighting coefficients, k = 0,1,...,M
M = filter order
In a practical application, the input and output discrete-time signals will be sampled at some reg-
ular sampling time interval, T seconds, denoted x[nT] and y[nT], which is related to the sampling
frequency by f
s
= 1/T, samples per second. However, for generality, it is more convenient to
assume that T is unity, so that the effective sampling frequency also is unity and the Nyquist fre-
quency is one-half. It is, then, straightforward to scale, by multiplication, this normalized fre-
quency range, i.e. [0, 1/2], to any other sampling frequency.
The output of the simple moving average filter is the average of the M + 1 most recent values
of x[n]. Intuitively, this corresponds to a smoothed version of the input, but its operation is more
appropriately described by calculating the frequency response of the filter. First, however, the z-
domain representation of the filter is introduced in analogy to the s- (or Laplace) domain repre-
sentation of analog filters. The z-transform of a causal discrete-time signal x[n] is defined by:
(6.2.2)
Where:
X(z) = z-transform of x[n]
z = complex variable
The z-transform of a delayed version of x[n], namely x[n – k] with k a positive integer, is found to
be given by z
–k
X(z). This result can be used to relate the z-transform of the output, y[n], of the
simple moving average filter to its input:
(6.2.3)
The z-domain transfer function, namely the ratio of the output to input transform, becomes:
(6.2.4)
y n
[ ]
b
k
x n
k
–
[
]
k
0
=
M
∑
=
b
k
1
M
1
+
--------------
=
X z
( )
x n
[ ]z
n
–
n
0
=
∞
∑
=
Y z
( )
b
k
z
k
–
X z
( )
k
0
=
M
∑
=
b
k
1
M
1
+
--------------
=
H z
( )
Y z
( )
X z
( )
-----------
b
k
z
k
–
k
0
=
M
∑
=
=
b
k
1
M
1
+
--------------
=
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
Digital Filters
Digital Filters 6-17
Notice the transfer function, H(z), is entirely defined by the values of the weighting coefficients,
b
k
, k = 0,1,...,M, which are identical to the discrete impulse response of the filter, and the com-
plex variable z. The finite length of the discrete impulse response means that the transient
response of the filter will last for only M + 1 samples, after which a steady state will be reached.
The frequency-domain transfer function for the filter is found by setting
(6.2.5)
Where
and can be written as:
(6.2.6)
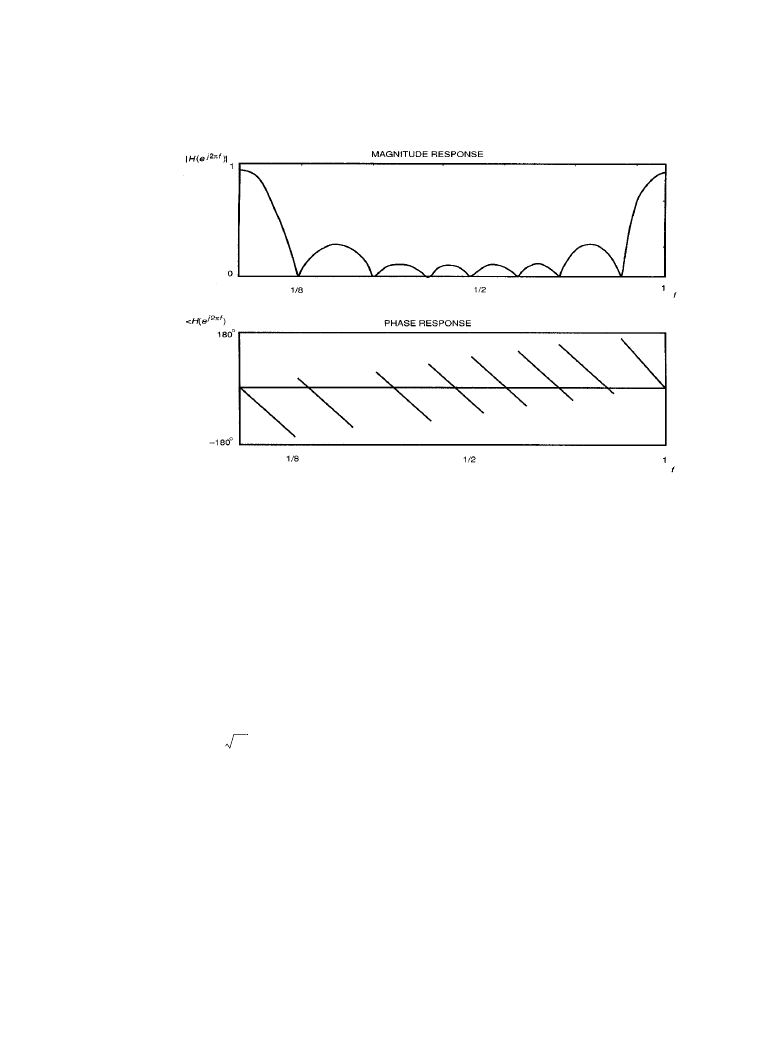
The magnitude and phase response of the simple moving average filter, with M = 7, are calcu-
lated from
and shown in Figure 6.2.1. The filter is seen clearly to act as a crude low-
pass smoothing filter with a linear phase response. The sampling frequency periodicity in the
magnitude and phase response is a property of discrete-time systems. The linear phase response
is due to the
term in
and corresponds to a constant M/2 group delay through
z
e
j2
πf
=
j
1
–
=
H e
j2
πf
(
)
1
M
1
+
--------------
e
j2
πfk
–
k
0
=
M
∑
1
M
1
+
--------------e
j
πfM
–
πf M 1
+
(
)
[
]
sin
πf
( )
sin
-------------------------------------
=
=
H e
j2
πf
(
)
e
j
πfM
–
H e
j2
πf
(
)
Figure 6.2.1
The magnitude and phase response of the simple moving average filter with
M = 7.
(
From [1]. Used with permission.)
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
Digital Filters

6-18 Digital Coding of Audio Signals
the filter. A phase discontinuity of
±180° is introduced each time the magnitude term changes
sign. FIR filters that have center symmetry in their weighting coefficients have this constant fre-
quency-independent group-delay property that is desirable in applications in which time disper-
sion is to be avoided, such as in pulse transmission, where it is important to preserve pulse shapes
[2].
6.2.2a
Design Techniques
Linear-phase FIR filters can be designed to meet various filter specifications, such as low-pass,
high-pass, bandpass, and band-stop filtering [1]. For a low-pass filter, two frequencies are
required. One is the maximum frequency of the passband below which the magnitude response
of the filter is approximately unity, denoted the passband corner frequency f
p
. The other is the
minimum frequency of the stop-band above which the magnitude response of the filter must be
less than some prescribed level, named the stop-band corner frequency f
s
. The difference
between the passband and stop-band corner frequencies is the transition bandwidth. Generally,
the order of an FIR filter, M, required to meet some design specification will increase with a
reduction in the width of the transition band. There are three established techniques for coeffi-
cient design:
•
Windowing. A design method that calculates the weighting coefficients by sampling the ideal
impulse response of an analog filter and multiplying these values by a smoothing window to
improve the overall frequency-domain response of the filter.
•
Frequency sampling. A technique that samples the ideal frequency-domain specification of
the filter and calculates the weighting coefficients by inverse-transforming these values.
•
Optimal approximations.
The best results generally can be obtained with the optimal approximations method. With the
increasing availability of desktop and portable computers with fast microprocessors, large quan-
tities of memory, and sophisticated software packages, optimal approximations is the preferred
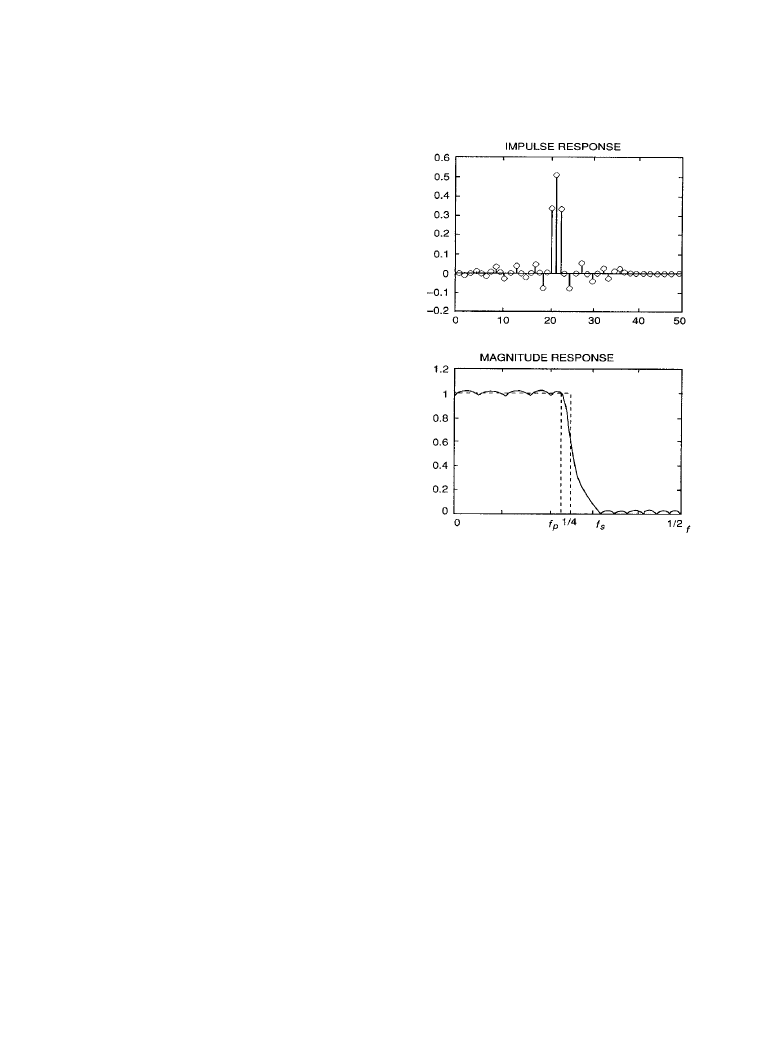
method for weighting coefficient design. The impulse response and magnitude response for a
40
th
-order optimal half-band FIR low-pass filter designed with the Parks-McClellan algorithm
[3] are shown in Figure 6.2.2, together with the ideal frequency-domain design specification.
Notice the zeros in the impulse response. This algorithm minimizes the peak deviation of the
magnitude response of the design filter from the ideal magnitude response. The magnitude
response of the design filter alternates about the desired specification within the passband and
above the specification in the stop-band. The maximum deviation from the desired specification
is equalized across the passband and stop-band; this is characteristic of an optimal solution.
6.2.2b
Applications
In general, digitally implemented FIR filters exhibit the following attributes [1]:
•
Absence of drift
•
Reproducibility
•
Multirate realizations
•
Ability to adapt to time-varying environments
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
Digital Filters
Digital Filters 6-19
These features have led to the widespread use of FIR filters in a variety of applications, particu-
larly in telecommunications. The primary advantage of the fixed-coefficient FIR filter is its
unconditional stability because of the lack of feedback within its structure and its exact linear
phase characteristics. Nonetheless, for applications that require sharp, selective, filtering—in
standard form—they do require relatively large orders. For some applications, this may be pro-
hibitive; therefore, recursive IIR filters are a valuable alternative.
6.2.2c
Finite Wordlength Effects
Practical digital filters must be implemented with finite precision numbers and arithmetic [1].
As a result, both the filter coefficients and the filter input and output signals are in discrete form.
This leads to four types of finite wordlength effects:
•
Discretization (quantization) of the filter coefficients has the effect of perturbing the location
of the filter poles and zeroes. As a result, the actual filter response differs slightly from the
ideal response. This deterministic frequency response error is referred to as coefficient quan-
tization error.
•
The use of finite precision arithmetic makes it necessary to quantize filter calculations by
rounding or truncation. Roundoff noise is that error in the filter output that results from
rounding or truncating calculations within the filter. As the name implies, this error looks like
low-level noise at the filter output.
Figure 6.2.2
The impulse and magnitude
response of an optimal 40
th
-order half-band
FIR filter. (
From [1]. Used with permission.)
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
Digital Filters

6-20 Digital Coding of Audio Signals
•
Quantization of the filter calculations also renders the filter slightly nonlinear. For large
signals this nonlinearity is negligible, and roundoff noise is the major concern. However,
for recursive filters with a zero or constant input, this nonlinearity can cause spurious oscil-
lations called limit cycles.
•
With fixed-point arithmetic it is possible for filter calculations to overflow. The term over-
flow oscillation refers to a high-level oscillation that can exist in an otherwise stable filter
because of the nonlinearity associated with the overflow of internal filter calculations.
Another term for this is adder overflow limit cycle.
6.2.3
Infinite Impulse Response Filters
A digital filter with impulse response having infinite length is known as an infinite impulse
response filter [1]. Compared to an FIR filter, an IIR filter requires a much lower order to
achieve the same requirement of the magnitude response. However, whereas an FIR filter is
always stable, an IIR filter may be unstable if the coefficients are not chosen properly. Because
the phase of a stable causal IIR filter cannot be made linear, FIR filters are preferable to IIR
filters in applications for which linear phase is essential.
Practical direct form realizations of IIR filters are shown in Figure 6.2.3. The realization
shown in Figure 6.2.3a is known as direct form I. Rearranging the structure results in direct
form II, as shown in Figure 6.2.3b. The results of transposition are transposed direct form I and
transposed direct form II, as shown in Figures 6.2.3c and 6.2.3d, respectively. Other realiza-
tions for IIR filters are state-space structure, wave structure, and lattice structure. In some sit-
uations, it is more convenient or suitable to use software realizations that are implemented by
programming a general-purpose microprocessor or a digital signal processor. (See [1] for
details on IIR filter implementations.)
Designing an IIR filter involves choosing the coefficients to satisfy a given specification,
usually a magnitude response parameter. There are various IIR filter design techniques,
including:
•
Design using an analog prototype filter, in which an analog filter is designed to meet the
(analog) specification and the analog filter transfer function is transformed to a digital sys-
tem function.
•
Design using digital frequency transformation, which assumes that a given digital low-pass
filter is available, and the desired digital filter is then obtained from the digital low-pass fil-
ter by a digital frequency transformation.
•
Computer-aided design (CAD), which involves the execution of algorithms that choose the
coefficients so that the response is as close as possible to the desired filter.
The first two methods are easily accomplished; they are suitable for designing standard filters
(low-pass, high-pass, bandpass, and band-stop). The CAD approach, however, can be used to
design both standard and nonstandard filters.
Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)
Copyright © 2004 The McGraw-Hill Companies. All rights reserved.
Any use is subject to the Terms of Use as given at the website.
Digital Filters