Файл: Audio and Radio Engineering.pdf

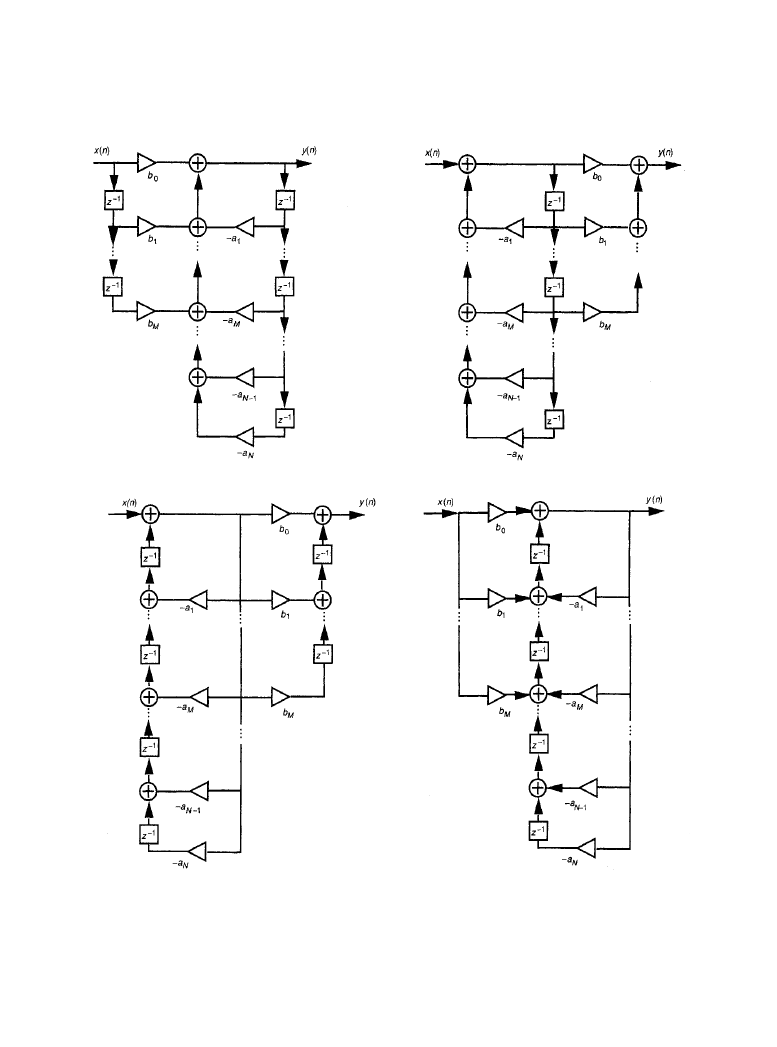
Digital Filters 6-21

Figure 6.2.3

 Direct form realizations of IIR filters: (

a) direct form I, (b) direct form II, (c) trans-

posed direct form I, (

d) transposed direct form II. (From [1]. Used with permission.)

(

b)

(

c)

(

d)

(

a)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Digital Filters

6-22 Digital Coding of Audio Signals

6.2.4

Reference

1.

Chambers, J. A., S. Tantaratana, and B. W. Bomar: “Digital Filters,” The Electronics Hand-
book, Jerry C. Whitaker (ed.), CRC Press, Boca Raton, Fla., pp. 749–772, 1996.

2.

Lee, E. A., and D. G. Messerschmitt: Digital Communications, 2

nd

 ed., Kluwer, Norell,

Mass., 1994.

3.

Parks, T. W., and J. H. McClellan: “A Program for the Design of Linear Phase Infinite
Impulse Response Filters,” IEEE Trans. Audio Electroacoustics, AU-20(3), pp. 195–199,
1972.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Digital Filters

6-23

Chapter

6.3

Digital Modulation

Rodger E. Ziemer, Oktay Alkin

Jerry C. Whitaker, Editor-in-Chief

6.3.1

Introduction

Digital modulation is necessary before digital data can be transmitted through a channel, be it a
satellite link or HDTV. Modulation is the process of varying some attribute of a carrier waveform
as a function of the input intelligence to be transmitted. Attributes that can be varied include
amplitude, frequency, and phase.

6.3.2

Digital Modulaton Techniques

With digital modulation, the message sequence is a stream of digits, typically of binary value [1].
In the simplest case, parameter variation is on a symbol-by-symbol basis; no memory is
involved. Carrier parameters that can be varied under this scenario include the following:

•

Amplitude, resulting in amplitude-shift keying (ASK)

•

Frequency, resulting in frequency-shift keying (FSK)

•

Phase, resulting in phase-shift keying (PSK)

So-called higher-order modulation schemes impose memory over several symbol periods. Such
modulation techniques can be classified as binary or M-ary, depending on whether one of two
possible signals or M > 2 signals per signaling interval can be sent. (Binary signaling may be
defined as any signaling scheme in which the number of possible signals sent during any given
signaling interval is two. M-ary signaling, on the other hand, is a signaling system in which the
number of possible signals sent during any given signaling interval is M.) For the case of M-ary
modulation when the source digits are binary, it is clear that several bits must be grouped to
make up an M-ary word.

Another classification for digital modulation is coherent vs. noncoherent, depending upon

whether a reference carrier at the receiver coherent with the received carrier is required for

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Source: Standard Handbook of Audio and Radio Engineering

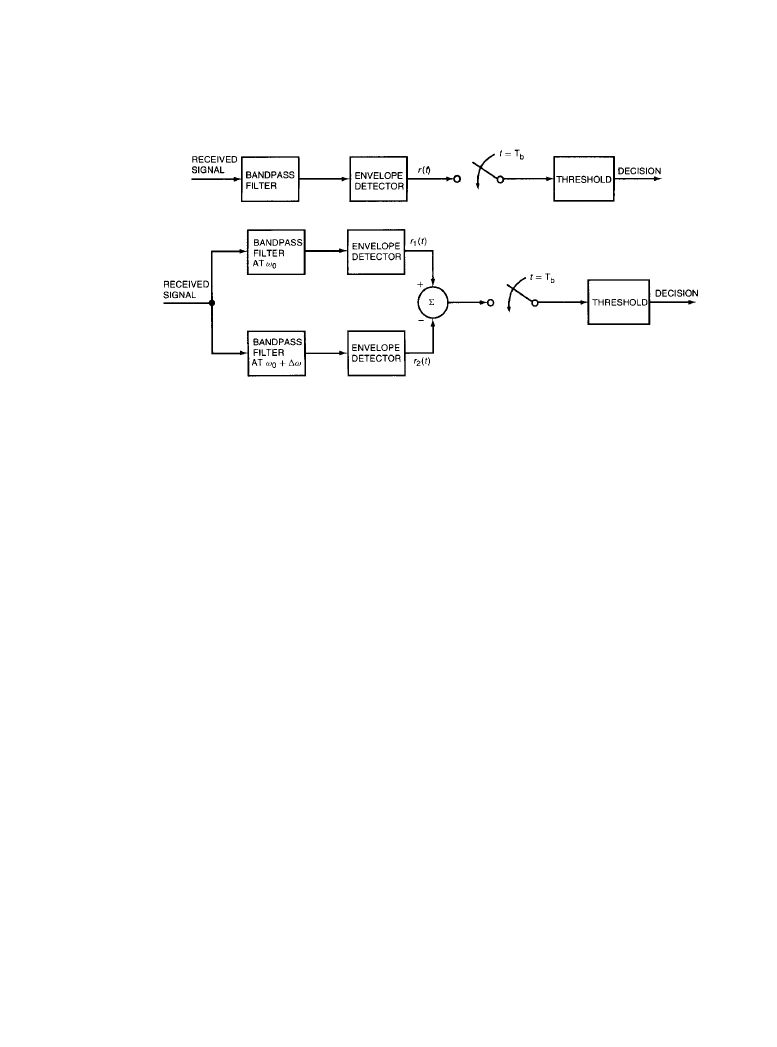
6-24 Digital Coding of Audio Signals

demodulation (the coherent case) or not (the noncoherent case). For situations in which it is dif-
ficult to maintain phase stability—for example, in channels subject to fading—it is useful to
employ a modulation technique that does not require the acquisition of a reference signal at the
receiver that is phase-coherent with the received carrier. ASK and FSK are two modulation tech-
niques that lend themselves well to noncoherent detection. Receivers for detection of ASK and
FSK noncoherently are shown in Figure 6.3.1.

One other binary modulation technique is, in a sense, noncoherent: differentially coherent

PSK (DPSK). With DPSK, the phase of the preceding bit interval is used as a reference for the
current bit interval. This technique depends on the channel being sufficiently stable so that phase
changes resulting from channel perturbations from a given bit interval to the succeeding one are
inconsequential. It also depends on there being a known phase relationship from one bit interval
to the next. This requirement is ensured by differentially encoding the bits before phase modula-
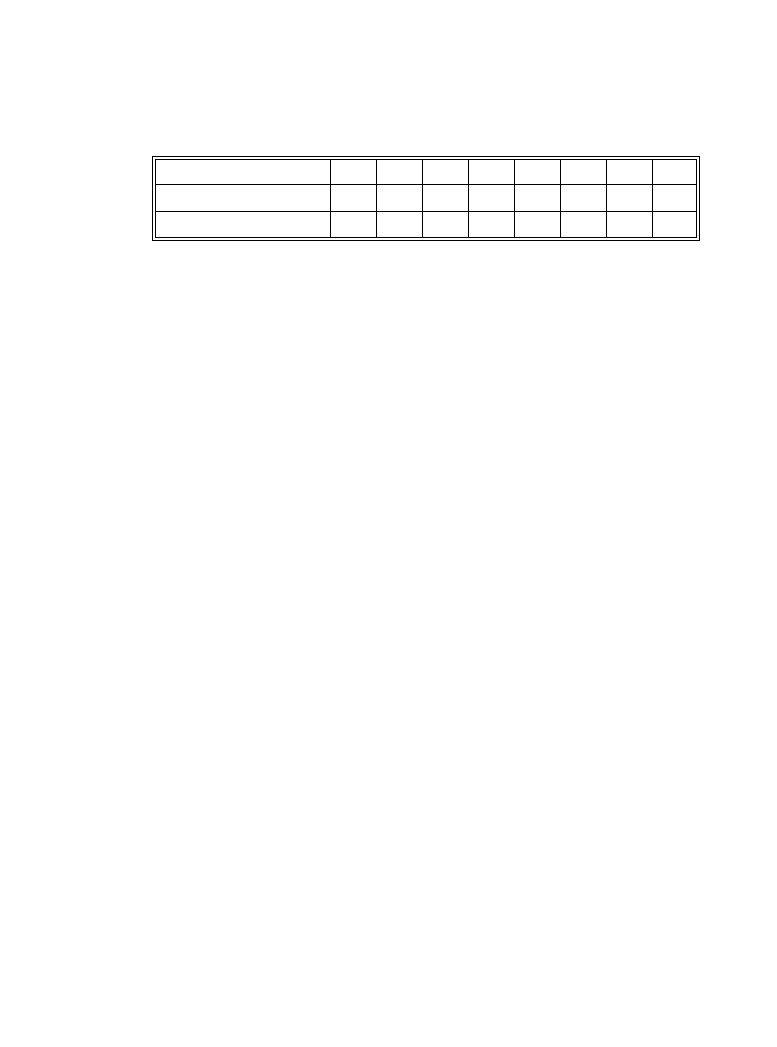
tion at the transmitter. Differential encoding is illustrated in Table 6.3.1. An arbitrary reference
bit is chosen to start the process. In the table a 1 has been chosen. For each bit of the encoded
sequence, the present bit is used as the reference for the following bit in the sequence. A 0 in the
message sequence is encoded as a transition from the state of the reference bit to the opposite
state in the encoded message sequence. A 1 is encoded as no change of state. Using these rules,
the result is the encoded sequence shown in the table.

6.3.2a

QPSK

Consider the case of an MPSK signal where M = 4, commonly referred to as quadriphase-shift
keying (QPSK) [1]. This common modulation technique utilizes four signals in the signal set dis-
tinguished by four phases 90

°  apart. For the case of an MASK signal where M = 4, a quadrature-

amplitude-shift keying (QASK) condition results. With QASK, both the phase and amplitude of

Figure 6.3.1 

Receiver systems for noncoherent detection of binary signals: (

a) ASK, (b) FSK.

(

From [1]. Used with permission.)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Digital Modulation

Digital Modulation 6-25

the carrier take on a set of values in one-to-one correspondence with the digital data to be trans-
mitted.

Several variations of QPSK have been developed to meet specific operational requirements.

One such scheme is referred to as offset QPSK (OQPSK) [2]. This format is produced by allow-
ing only 

±90°  phase changes in a QPSK format. Furthermore, the phase changes can take place

at multiples of a half-symbol interval, or a bit period. The reason for limiting phase changes to
±90°  is to prevent the large envelope deviations that occur when QPSK is filtered to restrict side-
lobe power, and regrowth of the sidelobes after amplitude limiting is used to produce a constant-
envelope signal. This condition often is encountered in satellite systems in which, because of
power-efficiency considerations, hard limiting repeaters are used in the communications system.

Another modulation technique closely related to QPSK and OQPSK is minimum shift keying

(MSK) [2]. MSK is produced from OQPSK by weighting the in-phase and quadrature compo-
nents of the baseband OQPSK signal with half-sinusoids. The phase changes linearly over a bit
interval. As with OQPSK, the goal of MSK is to produce a modulated signal with a spectrum of
reduced sidelobe power, one that behaves well when filtered and limited. Many different forms
of MSK have been proposed and investigated over the years.

A modulation scheme related to 8-PSK is 

π/4-differential QPSK (π/4-DQPSK) [3]. This tech-

nique is essentially an 8-PSK format with differential encoding where, from a given phase state,
only specified phase shifts of 

±π/4 or ± 3π/4 are allowed.

Continuous phase modulation (CPM) [4] comprises a host of modulation schemes. These for-

mats employ continuous phase trajectories over one or more symbols to get from one phase to
the next in response to input changes. CPM schemes are employed in an attempt to simulta-
neously improve power and bandwidth efficiency.

6.3.2b

Signal Analysis

The ideal choice of a modulation technique depends on many factors. Two of the most basic are
the bandwidth efficiency and power efficiency. These parameters are defined as follows:

•

Bandwidth efficiency is the ratio of the bit rate to the bandwidth occupied for a digital modu-
lation scheme. Technically, it is dimensionless, but for convenience it is usually given the
dimensions of bits/second/hertz.

•

Power efficiency is the energy per bit over the noise power spectral density (E

b

/N

o

) required

to provide a given probability of bit error for a digital modulation scheme.

Computation of these parameters is beyond the scope of this chapter. Interested readers are
directed to [1] for a detailed discussion of performance parameters.

Table 6.3.1 Example of the differential encoding process 

(

After [1].

)

Message Sequence

1

0

0

1

1

1

0

Encoded Sequence

1

1

0

1

1

1

1

0

Transmitted Phase Radians

0

0

p

0

0

0

0

p

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Digital Modulation