Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 142
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
x x hi xi xi1 , i 1, n:


i i1 2 2
b n
IS f xdx hif xi .
a i1
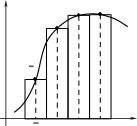
Пример геометрической интерпретации метода средних прямоугольни- ков представлен на рис. 3.
 y y fx
y y fx
fx1
x0 x1
x1 xnx
Рис. 3. Пример метода средних прямоугольников.
В случае постоянного шага интегрирования, когда
h h b a,
 i n
i n
i 1, n, формула средних прямоугольников будет иметь следующий вид
b n
IS fxdx h fxi,
a
где x a h i 1 , i 1, n.


i1
i 2
Из трех рассмотренных выше методов в подавляющем большинстве случаев метод средних прямоугольников является наиболее точным.
Замечание. Если подынтегральная функция
fx
задана не
аналитическим выражением, а таблично, то формула средних прямоугольников оказывается неприменима (без привлечения дополнительной интерполяции), так как значения функции известны лишь в узловых точках. В этом случае пользуются либо формулами левых или правых прямоугольников, либо используют другие методы.
На каждом частичном отрезке интегрирования xi1, xi,
i 1, n, заме-
ним подынтегральную функцию
fx
полиномом первой степени
ix –
прямой линией, проходящей через точки xi1 , fi1 и xi, fi:
fx
x f
fi1 x x
, i 1, n.
i i1
xi x
i1
i1
Пояснение. В общем виде уравнение прямой линии, проходящей через две точки x1, y1 и x2 , y2 , задается следующим образом:
y y1
x x1
, откуда y y y2 y1 x x.
2
y2 y1
x2 x1
1 x
x1
1
Подставляя полученное выражение в формулу (3.1) и выполняя инте- грирование по частичным отрезкам, приходим к формуле трапеций:
b
1
n
2
IT f
a
xdx
hi
i1
fi1
fi , где hi
xi xi1 .
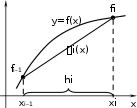
На отрезках xi1, xi,
i 1, n, площадь под графиком функции
y fx
заменяется площадями трапеций с основаниями, равными значениям функ-
ции
fx на концах отрезка, и высотой, равной hi
 y
y
(рис. 4).
Рис. 4. Иллюстрация метода трапеций.
В случае постоянного шага интегрирования, когда
i 1, n, формула трапеций принимает вид:
h h b a,
 i n
i n
b
h
n
2
h
IT f
a
xdx
i1
fi1 fi
2 f0
2 f1
2 f2
...
2 fn1
fn . (3.6)
Для удобства вычислений формулу (3.6) записывают следующим обра-
зом:
f0 fn
n1
IT f
xdx h
2
fi .
a i1
Вид представленной формулы позволяет сделать вывод, что она может быть сформирована также исходя из других соображений, так как получае- мый с ее применением результат является средним арифметическим резуль- татов использования формул левых (3.3) и правых (3.4) прямоугольников.
Поэтому
I IL IRT 2
и указанное утверждение справедливо для случаев
равных и неравных шагов интегрирования.
Замечание. Несмотря на то, что в методе трапеций для аппроксимации подынтегральной функции используются полиномы первой степени, по сравнению с методами прямоугольников, которые используют полиномы ну- левой степени, точность метода трапеций оказывается ниже точности метода средних прямоугольников. Более высокая точность метода средних прямо- угольников объясняется «удачным» выбором узловых точек для вычисления значений подынтегральной функции.
Аппроксимацию функции
fx
по методу трапеций можно
интерпретировать как замену исходной функции
fx
некоторой кусочно-
линейной функцией. Ошибка метода в данном случае определяется
«грубостью» предложенного способа аппроксимации функции. Естественно
допустить, что если исходную функцию
fx
аппроксимировать на


i i1 2 2
b n
IS f xdx hif xi .
a i1
Пример геометрической интерпретации метода средних прямоугольни- ков представлен на рис. 3.
 y y fx
y y fxfx1
x0 x1
x1 xnx
Рис. 3. Пример метода средних прямоугольников.
В случае постоянного шага интегрирования, когда
h h b a,
 i n
i ni 1, n, формула средних прямоугольников будет иметь следующий вид
b n
IS fxdx h fxi,
a
где x a h i 1 , i 1, n.


i1
i 2
Из трех рассмотренных выше методов в подавляющем большинстве случаев метод средних прямоугольников является наиболее точным.
Замечание. Если подынтегральная функция
fx
задана не
аналитическим выражением, а таблично, то формула средних прямоугольников оказывается неприменима (без привлечения дополнительной интерполяции), так как значения функции известны лишь в узловых точках. В этом случае пользуются либо формулами левых или правых прямоугольников, либо используют другие методы.
-
Метод трапеций
На каждом частичном отрезке интегрирования xi1, xi,
i 1, n, заме-
ним подынтегральную функцию
fx
полиномом первой степени
ix –
прямой линией, проходящей через точки xi1 , fi1 и xi, fi:
fx
x f
-
fi
fi1 x x
, i 1, n.
i i1
xi x
i1
i1
Пояснение. В общем виде уравнение прямой линии, проходящей через две точки x1, y1 и x2 , y2 , задается следующим образом:
y y1
x x1
, откуда y y y2 y1 x x.
2
y2 y1
x2 x1
1 x
x1
1
Подставляя полученное выражение в формулу (3.1) и выполняя инте- грирование по частичным отрезкам, приходим к формуле трапеций:
b
1
n
2
IT f
a
xdx
hi
i1
fi1
fi , где hi
xi xi1 .
На отрезках xi1, xi,
i 1, n, площадь под графиком функции
y fx
заменяется площадями трапеций с основаниями, равными значениям функ-
ции
fx на концах отрезка, и высотой, равной hi
 y
y(рис. 4).
Рис. 4. Иллюстрация метода трапеций.
В случае постоянного шага интегрирования, когда
i 1, n, формула трапеций принимает вид:
h h b a,
 i n
i nb
h
n
2
h
IT f
a
xdx
i1
fi1 fi
2 f0
2 f1
2 f2
...
2 fn1
fn . (3.6)
Для удобства вычислений формулу (3.6) записывают следующим обра-
зом:
b
f0 fn
n1
IT f
xdx h
2
fi .
a i1
Вид представленной формулы позволяет сделать вывод, что она может быть сформирована также исходя из других соображений, так как получае- мый с ее применением результат является средним арифметическим резуль- татов использования формул левых (3.3) и правых (3.4) прямоугольников.
Поэтому
I IL IRT 2
и указанное утверждение справедливо для случаев
равных и неравных шагов интегрирования.
Замечание. Несмотря на то, что в методе трапеций для аппроксимации подынтегральной функции используются полиномы первой степени, по сравнению с методами прямоугольников, которые используют полиномы ну- левой степени, точность метода трапеций оказывается ниже точности метода средних прямоугольников. Более высокая точность метода средних прямо- угольников объясняется «удачным» выбором узловых точек для вычисления значений подынтегральной функции.
-
Метод Симпсона (метод парабол)
Аппроксимацию функции
fx
по методу трапеций можно
интерпретировать как замену исходной функции
fx
некоторой кусочно-
линейной функцией. Ошибка метода в данном случае определяется
«грубостью» предложенного способа аппроксимации функции. Естественно
допустить, что если исходную функцию
fx
аппроксимировать на