Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 139

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



    1. 1   2   3   4   5   6   7   8   9   ...   15

Площадь поверхности вращения





Если дуга гладкой кривой

y f(x) ,

a x b, вращается вокруг оси

Ox, то площадь поверхности вращения вычисляется по формуле

b

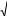Sx 2 y

a

1 y2 dx

Пример. Найти площадь поверхности, образованной вращением вокруг оси

Oxплоской фигуры ограниченной линиями

y x3,

x 0,

x 2 .

Найдем производную

y 3x2 , тогда

2 2

2 2 1

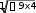S 2 x3

dx 2 x3



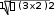
dx

19x4 2d1 9x4





x  

36

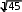0 0 0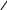


2
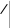 2 1  9x4 32

14532 1

145

1

18 3

0 27 27



Для решения подобных задач в Maxima следует выполнить следую- щиедействия:

      1. Построить кривую.

      2. Вычислить производные функции.

      3. В зависимости от способа задания кривой, составить и вычис- литьопределенный интеграл с помощью программы Maxima и вручную.

      4. Записать ответ.

Пример 11. Найти площадь поверхности, образованной вращением вокруг

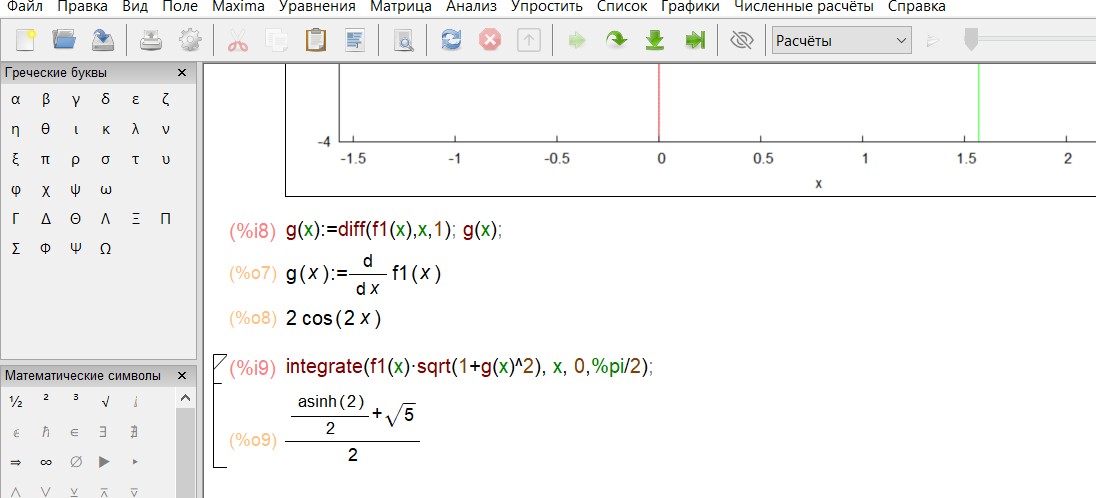
оси Oxдуги кривой ???? = sin 2???? от ???? = 0 до ???? = .

2

Введем функции:




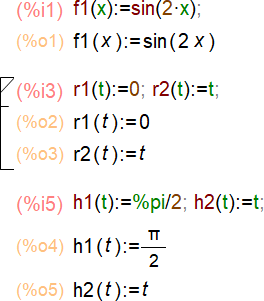
Построим график функций:




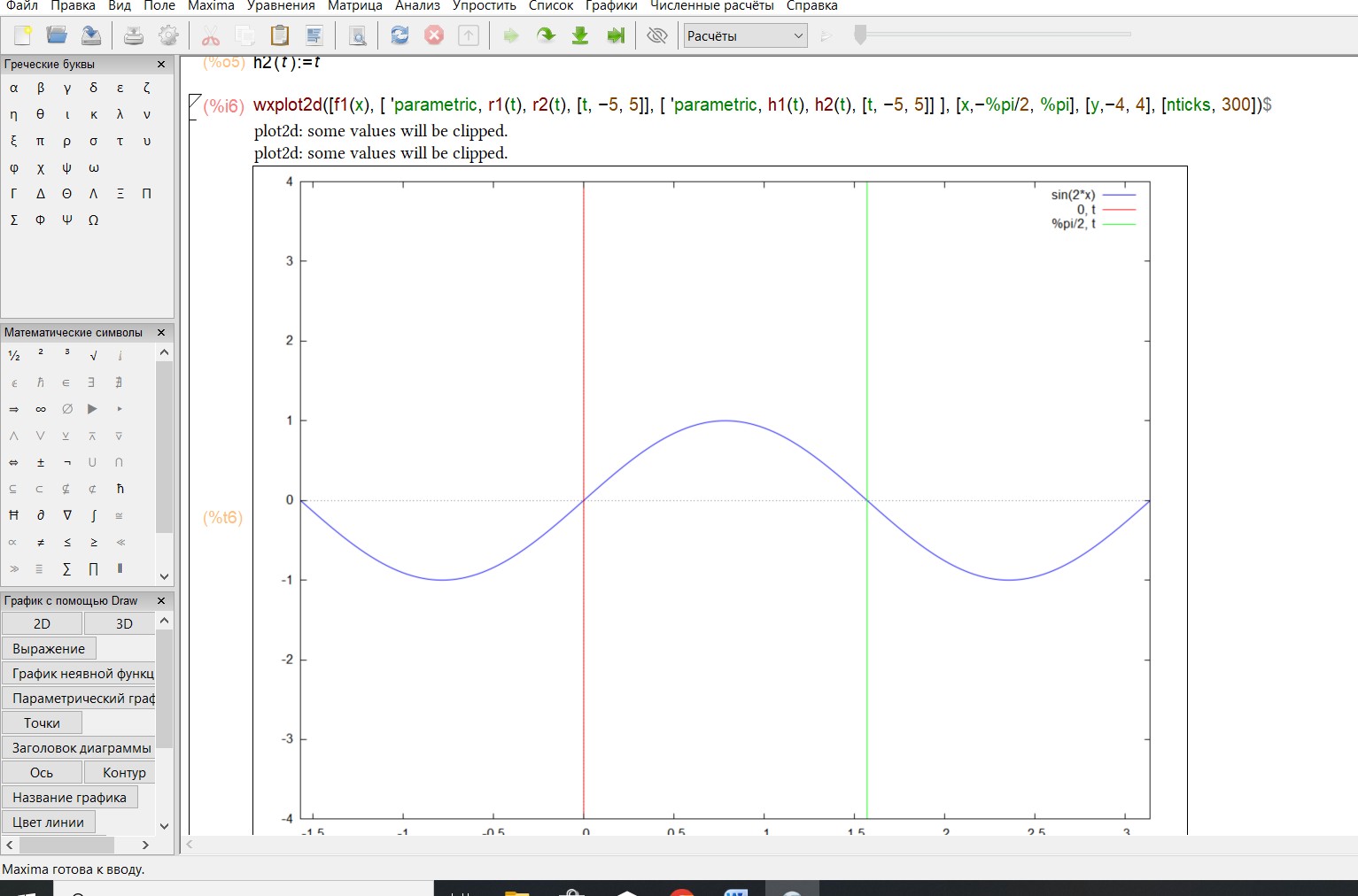
Найдем производную и вычислим интеграл



Справочная информация:


ex e x

Гиперболический косинус:

ch x .

2

ex e x

Гиперболический синус:

sh x .

2

Гиперболический тангенс:

th x

sh x


ch x

ex e x

ex e x

ch x

ex e x

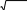
Гиперболический котангенс:

cth x sh xex e x .

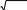Гиперболический ареасинус: Arsh x ln xx2 1

Гиперболический ареакосинус:

Arch x lnx

x2 1  lnx

x2 1

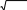Гиперболический ареатангенс:

Arth x 1 ln 1 x



2 1 x

Гиперболический ареакотангенс:

Arcth x 1 ln x 1



2 x1

2. Приближенные вычисления определенных интегралов

    1. Некоторые теоретические сведения


Если функция

y fx

непрерывна на отрезке a,b

и известна ее


первообразная F(x) , то определенный интеграл удается вычислить
непосредственно с помощью формулы Ньютона-Лейбница:


b




fxdx Fb Fa,

a

где

Fb и

Fa

  • значения первообразной

Fx

функции

fx

на концах


отрезка интегрирования.

Однако во многих случаях в реальных исследовательских задачах первообразная функции F(x) не может быть выражена через элементарные функции или является слишком сложной; вследствие этого вычисление определенного интеграла по формуле Ньютона-Лейбница может быть затруднительным или невыполнимым. Кроме того, на практике подынтегральная функция f(x) часто задается таблично и тогда само понятие первообразной теряет смысл. Поэтому большое значение имеют приближенные и в первую очередь численные методы вычисления определенных интегралов.

Назначение большинства приближенных методов вычисления

определенных интегралов состоит в замене подынтегральной функции

fx

аппроксимирующей функцией

x, для которой можно легко записать

первообразную в элементарных функциях, то есть
b b

I fxdx xdx R,

a a

где R– погрешность вычисления интеграла.

Чаще всего функцию

fx

заменяют интерполяционным полиномом


(под интерполяцией понимают приближенное вычисление неизвестных зна- чений функции по известным ее значениям в заданных точках), для построе-

ния которого используются значения функции в узлах


  1. , i 0, n:


где
rx – остаточный член.

fx fxi rx,


n
i0

Подставляя полученное выражение в определенный интеграл вместо подынтегральной функции, получим общую формулу численного интегрирования

b n

I f xdx Aif xi R,

a i0

где

fxi

  • значения подынтегральной функции в узловых точках

xi ,

Ai –

весовые коэффициенты, а R– погрешность или остаточный член формулы.

С целью уменьшения погрешности, связанной с заменой

подынтегральной функции, отрезок интегрирования a,b

разбивают на n

отрезков и на каждом из полученных (частичных) отрезков xi1, xi, заменяют подынтегральную функцию аппроксимирующей функцией

i 1, n,

ix.

Смотрите также файлы