Файл: Методические указания по выполнению курсовой работы по дисциплине (модулю) Введение в математический анализ.docx

Скачать файл (2,85Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 140

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Тогда приближенное значение интеграла определяется суммой частичных

^{интегралов}^от^{функций}_ix^,^взятых^в^{пределах}^от

^xi1 ^до^xi

для i 1, n:

b _n^x_i

I _fxdx ___ixdx. (3.1)

_ai1 _x_i_₁

Методы численного интегрирования можно классифицировать в зависимости

от способа аппроксимации подынтегральной функции ^{функций}_ix^,i 1, n^.

fx

с помощью

Методы Ньютона-Котеса основаны на полиномиальной

аппроксимации подынтегральной функции. Методы данного класса отличаются друг от друга степенью используемого полинома, от которой

зависит количество узлов, в которых необходимо вычислять функцию

fx.

В методах Ньютона-Котеса отрезок интегрирования разбивается, как правило, на отрезки равной длины, величина которых определяется как

_h_b a

n
и называется шагом интегрирования. Алгоритмы данных методов

просты и легко поддаются программной реализации.

В процессе численного интегрирования необходимо вычислить приближенное значение интеграла и оценить погрешность R . Погрешность, возникающая при численном интегрировании (также как и при численном дифференцировании), имеет два основных источника. Первым источником погрешности является замена подынтегральной функции аппроксимирующей функцией – погрешность аппроксимации. Как будет показано далее, погрешность аппроксимации уменьшается с увеличением количества nотрезков разбиения исходного отрезка интегрирования за счет более точной аппроксимации подынтегральной функции. Второй источник погрешности – неточности в вычислении подынтегральной функции в узловых точках и ошибки округления. Данная погрешность возрастает с ростом nи с

некоторого значения

n^* ^{начинает преобладать над погрешностью}

аппроксимации. Это обстоятельство должно предостеречь от выбора чрезмерно большого числа n.

Способ получения формул для вычисления приближенного значения

интеграла в методах Ньютона-Котеса состоит в следующем. Разобьем

отрезок интегрирования a,b

на n частичных (как правило, равных по

длине) отрезков, точки разбиения

x₀, x₁,..., x_n^,

a x₀^,

b x_n

будем называть

узлами интегрирования, а расстояния между узлами

h_i x_i x_i_₁,

i 1, n, –

шагамиинтегрирования. В частном случае шаг интегрирования может быть

постоянным ( h ^b^^a). На каждом из частичных отрезков интегрирования

n

x_i_₁, x_i,

i 1, n, будем аппроксимировать подынтегральную функцию

полиномом некоторой степени. В результате вычисление частичных интегралов на отрезках x_i_₁, x_i, i 1, n, по формуле (3.1) не составит труда.

Методы численного интегрирования
1. Методы прямоугольников

Рассмотрим простейшие методы из класса методов Ньютона-Котеса, в

которых подынтегральную функцию

fx

на отрезках интегрирования

x_i_₁, x_i^,

i 1, n, заменяют полиномом нулевой степени (константой):

fx  _ix  c_i^.^{Подставляя}интегрирование, получаем

_ix

в формулу (3.1) и выполняя

n

i

n

n

b

n
x

  ^x 

I _f

a

xdx _c_i

i1

_dx_c_ix

_xi1

i

^xi1

 _c_i

i1

^xi^^xi1

 _c_ih_i. (3.2)

i1

i1

Таким образом, в геометрической интерпретации приближенное значение интеграла определяется суммой площадей прямоугольников, одна из сторон которых соответствует отрезкам интегрирования длиной

h_i x_i x_i_₁^,^а^другая^–^{аппроксимирующим}^{константам.}^Отсюда^{происходит}

и название методов.

Далее будем использовать обозначения:
^fi1 ^
fx_i_₁^,
f_i
fx_i^,

^fi1 ^

f x_i_₁^.

Заметим, что замена подынтегральной функции константой неодно-

значна, так как ее можно выбрать равной значению подынтегральной функ- ции в любой точке каждого частичного отрезка интегрирования. Выбирая

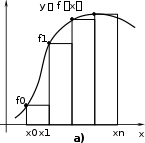
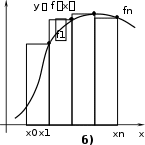y _y

Рис. 1. Пример метода левых (а) и правых (б) прямоугольников

^{константу}с_i

равной значению подынтегральной функции в левой (рис. 1 а)

^и^л^и^п^р^ав^о^й⁽^р^и^с.¹^б)^г^р^а^н^и^ц^а^х^отре^з^к^о^вx_i_₁, x_i^,

i 1, n, приходим к форму-

лам левых и правых прямоугольников, соответственно:

b _n

I_L _fxdx _h_if_i_₁ h₁f₀ h₂f₁ ...  h_nf_n_₁, (3.3)

i1
_n

I_R _fxdx _h_if_i

 h₁f₁ h₂f₂ ...  h_nf_n. (3.4)

n
_ai1

В случае постоянного шага интегрирования, когда h_i

i 1, n, формулы (3.3) и (3.4) приобретают вид

__h_b a _,

b _n

I_L _fxdx h_f_i_₁ h f₀

f₁  ... 

^fn1 ^^,

i1

(3.5)

I_R _fxdx h_f_i

 h f₁

f₂  ... 

f_n.

_ai1

На рис. 2 закрашенными фигурами показаны примеры погрешности вычисления значений интеграла методами левых и правых прямоугольников.

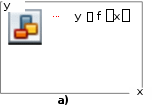
^yy fx

x

б)

Рис. 2. Пример погрешности метода левых (а) и правых (б) прямоугольников.
Наиболее широко на практике используется формула средних

прямоугольников, в которой значение константы с_i

(высоты

прямоугольника) выбирается равной значению подынтегральной функции в

средней точке x_i

каждого частичного отрезка интегрирования