Y=N*α=20*0,03=0,6 Эрл (по табл. Энгсета)

Вывод:

Примитивный поток обслуживается эффективнее, чем простейший, т.к. нагрузка примитивного потока выше, чем нагрузка простейшего.

С увеличением числа источников нагрузки, величина поступающей нагрузки уменьшается.

При неограниченном увеличении числа источников, величина нагрузки примитивного потока стремится к нагрузке простейшего потока.

Задача 4

На вход коммутационной системы поступает нагрузка по двум пучкам линий, математическое ожидание которой 20 эрланг и 60 эрланг. На выходе ступени объединенная нагрузка распределяется по направлениям пропорционально коэффициентам 0,1, 0,15, 0,25 и 0,5. Определить расчетное значение нагрузки каждого направления и относительное отклонение расчетного значения нагрузки от ее математического ожидания. По результатам расчета сделать вывод.

Решение:

Суммарная средняя нагрузка, поступающая на вход коммутационной системы:



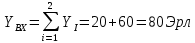
Рассчитаем математическое ожидание нагрузки на выходе ступени по направлениям:









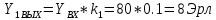
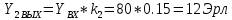
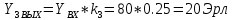
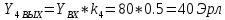
Расчетное значение нагрузки каждого направления:



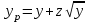
Чем больше значение аргумента z функции Лапласа, тем с большей вероятностью гарантируется нормированное качество обслуживания, однако при этом возрастает объем оборудования. В практике проектирования ГТС значение коэффициента принимается .











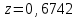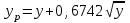
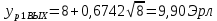
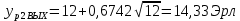
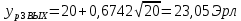
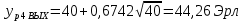
Относительное отклонение расчетного значения нагрузки от ее математического ожидания:

---

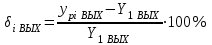
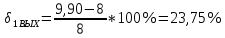
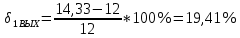
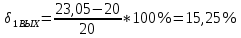
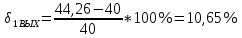
Вывод: чем больше нагрузка, тем меньше дисперсия. Если дисперсия расчетной нагрузки стремится к «0», то такая нагрузка называется сглаженной. И, следовательно, обслуживается лучше.

Задача 5

Определить нагрузку поступающую от тысячной линейной абонентской группы, если среднее число вызовов от одного абонента 3, среднее время разговора 100 с, доля вызовов закончившихся разговором 0,6. Нумерация на сети пяти- или шестизначная.

Решение:

Величина интенсивности нагрузки может быть рассчитана по формуле:



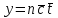
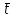- средняя длительность одного занятия на АТС в целом.

Для сокращения объема вычислений иногда пользуются приближенной формулой



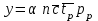
Если среднюю длительность занятий выразить в часах, то интенсивность нагрузки будет рассчитана в эрлангах. Коэффициент α учитывает непроизводительную нагрузку при занятиях, не окончившихся разговором. Величина α зависит от средней продолжительности разговора, доли вызовов, закончившихся разговором, 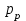, значности нумерации на сети, системы АТС.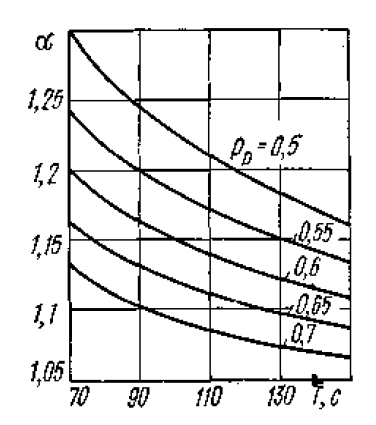



Рисунок 5.1 Зависимость коэффициента α от средней продолжительности разговора

Согласно графику на рисунке 5.1 при доли вызовов, закончившихся разговором, 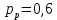и средней продолжительности разговора 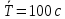коэффициент составил α=1,15

Средние длительности занятий, окончившихся разговором

,

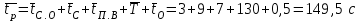где 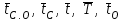– средние продолжительности соответственно слушания абонентом сигнала ответа станции, установления соединения, посылки вызова вызываемому абоненту, разговора, возвращения приборов в исходное состояние после отбоя. По данным наблюдений, на действующих сетях:

---

;

;

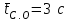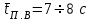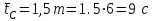, здесь m - число знаков абонентского номера; 1,5 - средняя продолжительность набора одной цифры номера с помощью дискового номеронабирателя, с;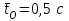



Нагрузка, поступающая от тысячной линейной абонентской группы



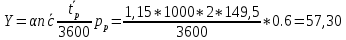
Ответ: Y=57,30 Эрл

Задача 6

На коммутационную систему поступает поток вызовов, создающий нагрузку 4,7 эрланга. Определить вероятности поступления ровно i вызовов Pi (i=0, 1, 2 ... N) при примитивном потоке от 10 источников и Pi (i=0,1, 2... j) при простейшем потоке вызовов. Построить кривые распределения вероятностей Pi =f(i) и произвести сравнение полученных результатов.

Решение:

1. 
   Для простейшего потока:
   

Pi= 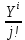* 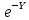= 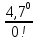* 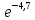=0,009

Для упрощения расчетов воспользуемся рекуррентной формулой:

Р0+1= 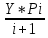=0,009

Р1+1= 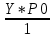= =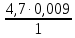0,042

Р2+1= 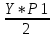= =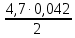0,098

Р3+1= 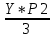= =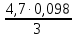0,154

Р4+1= 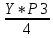= =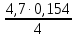0,180

Р5+1= 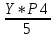= =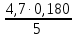0,170

Р6+1= 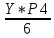= =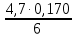0,133

Р7+1=

---

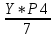
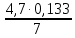= =0,089

Р8+1= 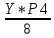= =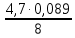0,052

Р9+1= 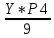= =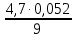0,027

Р10+1= 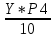= =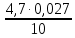0,013

P0+P1+P2+P3+P4+P5+P6+P7+P8+P9+P10=0.967 1(погрешность округления)

2. 
   Для примитивного потока:
   

Рi= *

=

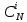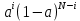
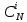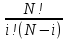
а = 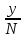- нагрузка, поступающая от одного источника

*

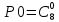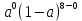
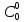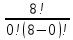= =1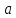

=4.7/10=0,47 Эрл

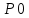=1∙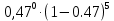 = 0.041

Для упрощения расчетов воспользуемся рекуррентной формулой:

Pi+1=

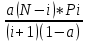
P0=0,041

P1= 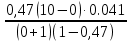=0,36

P2= 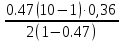=1.43

P3= 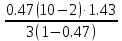=3.38

P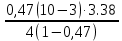4= =5.24

P5= 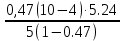=5.57

P6= 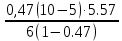=4.11

P7= 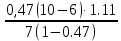=2.08

P8= 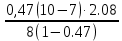=0.691

P9=

---

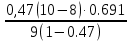
=0.136

P10= 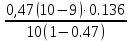=0.012

Р0+ P1+P2+P3+P4+P5+P6+P7+P8+P9+P10=23.05

Построим графики для обоих потоков:



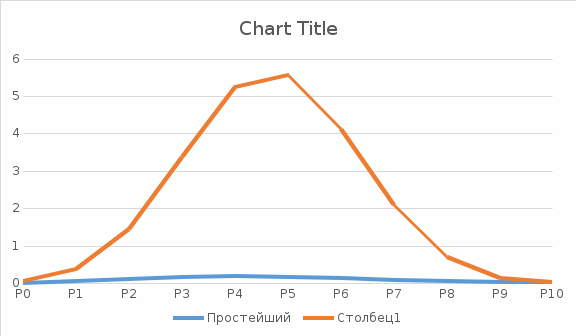
Рисунок 6.1 Кривые распределения вероятностей

Задача 7

На полнодоступный пучок емкостью 10 линий поступает простейший поток вызовов с параметром выз/час и выз/час. Время обслуживания распределено по экспоненциальному закону, средняя величина которого 90с. Постоянная обслуживания равна 1. Допустимое время ожидания начала обслуживания 90 с. Требуется определить:

• 
  Вероятность потерь по времени;
  
• 
  Вероятность занятия всех линий пучка;
  
• 
  Вероятность потерь по вызовам;
  
• 
  Вероятность того, что время ожидания начала обслуживания превысит t;
  
• 
  Среднее время ожидания начала обслуживания по отношению к любому вызову;
  
• 
  Среднее время ожидания начала обслуживания по отношению к задержанному вызову;
  
• 
  Среднюю длину очереди;
  
• 
  Вероятность того, что длина очереди превысит один вызов.
  

Дано: λ=600выз/час; t=90c; t_д=90с; V=10

Найти: Pi(i=0,v)-?; Wj(j=0,v)-?; P(γ>t)-?;M[j]-? M[γ]-?

Решение:

Находим поступающую нагрузку на СМО:

y=λ*t/3600=600*90/3600=15 Эрл

Определим вероятности занятности i линий в произвольный

Момент времени:



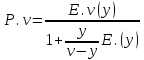
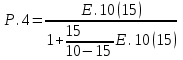_{- находим с помощью т. Пальма}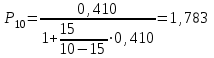



Для упрощения расчетов воспользуемся рекуррентной формулой:

P₉=P₄*(10/y)=1,783*(10/15)=1,188

P₈=P₉*(9/y)=1,188*(9/15)=0,713

P₇=P₈*(8/y)=0,713*(8/15)=0,38

P₆=P₇*(7/y)=0,38*(7/15)=0,177

P₅=P₆*(6/y)=0,177*(6/15)=0,071

P₄=P₅*(5/y)=0,071*(5/15)=0,024

P₃=P₄*(4/y)=0,024*(4/15)=0,0063

P₂=P₃*(3/y)=0,0063*(3/15)=0,0013

P₁=P₂*(2/y)=0,0013*(2/15)=0,0002

P₀=P₁*(1/y)=0,0002*(1/15)=0,00001

Вероятность того, что длина очереди составляет j-вызовов находится по формуле:

Wj=W_j-1*(y/v) ВероятностьW₀=P₄=1,783

W₁=W₀*(y/v)=1,783*(15/10)=2,674

W₂=W₁*(y/v)=2,674*(15/10)=4,011

W₃=W₂*(y/v)=4,011*(15/10)=6,016

W₄=W₃*(y/v)=6,016*(15/10)=9,024

W₅=W₄*(y/v)=9,024*(15/10)=13,537

W₆=W₅*(y/v)=13,537*(15/10)=20,305

W₇=W₆*(y/v)=20,305*(15/10)=30,458

W₈=W₇*(y/v)=30,458*(15/10)=45,686

---

Смотрите также файлы

• Лабораторная работа 1 "Стеганография" По дисциплине "Криптография" ст гр. Тзи20 Овсянников Д. В. Проверил.docx

• Профилактика суицидального поведения подростков.ppt

• 5 в случае реализации программы основного общего образования, в том числе адаптированной, с применением электронного обучения.docx

• Омлет овощи Каша орехи.docx

• При вложении капитала в мероприятие а из 120 случаев прибыль в 25 тыс р.docx