Файл: Контрольная работа По дисциплине Теория телетрафика Выполнил Группа Проверила Лизнева Ю. С.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 438
Скачиваний: 12
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
W9=W8*(y/v)=45,686*(15/10)=68,529
W10=W9*(y/v)=68,529*(15/10)=102,794
Находим функцию распределения времени ожидания начала обслуживания:
P(γ>t)=Pt*e-(v-y)t
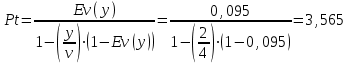
t=tд/t=90/90=1
Находим среднее время ожидания обслуживания:
M[γ]=Pt/(v-y)=3,565/(10-15)=0,713
Приведем время в абсолютные единицы:
M[γ]’= M[γ]*t=0,713*90=64,174c.
Находим длину очереди:
M[j]=Pt*y/(v-y)=0,713*2/(10-15)=10,696
Вывод: На основании приведенных расчетов можно сделать вывод, что
в системе с ожиданием из 1000 вызовов 3 будут находиться в очереди. Р(γ>0)>0,095, то есть вероятность того, что в системе с ожиданием поступающий вызов поступает на ожидание больше вероятности того, что в системе с потерями будет потерян.
W10=W9*(y/v)=68,529*(15/10)=102,794
Находим функцию распределения времени ожидания начала обслуживания:
P(γ>t)=Pt*e-(v-y)t
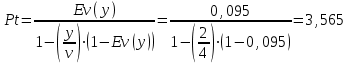
t=tд/t=90/90=1
Находим среднее время ожидания обслуживания:
M[γ]=Pt/(v-y)=3,565/(10-15)=0,713
Приведем время в абсолютные единицы:
M[γ]’= M[γ]*t=0,713*90=64,174c.
Находим длину очереди:
M[j]=Pt*y/(v-y)=0,713*2/(10-15)=10,696
Вывод: На основании приведенных расчетов можно сделать вывод, что
в системе с ожиданием из 1000 вызовов 3 будут находиться в очереди. Р(γ>0)>0,095, то есть вероятность того, что в системе с ожиданием поступающий вызов поступает на ожидание больше вероятности того, что в системе с потерями будет потерян.