Сопоставляя структурные схемы (16 и 19), получим соотношения между параметрами математической модели регулирующей части контура скорости в относительных единицах и параметрами элементов принципиальной схемы.

Для обеспечения единичных коэффициентов передачи в каналах задания скорости и обратной связи по скорости должны выполняться условия:



Для обеспечения требуемого коэффициента передачи регулятора скорости должно выполняться условие:



Из записанных соотношений выразим и рассчитаем сопротивления R₁₄, R₁₅ и R₁₆.



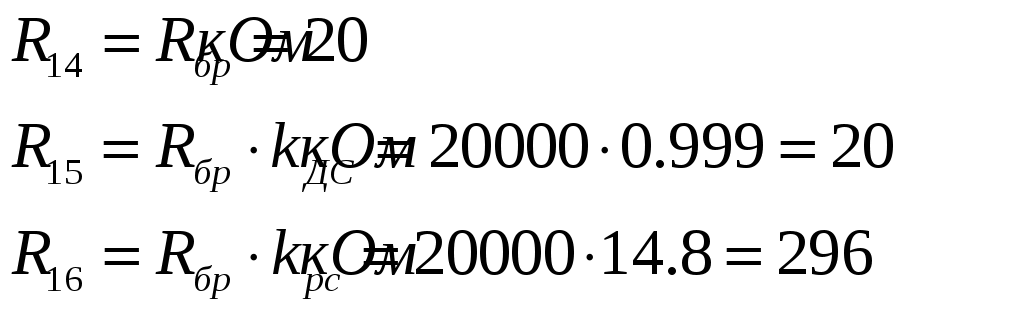
6.4 Расчет задатчика интенсивности

6.4.1. Расчет параметров математической модели задатчика интенсивности

Задатчик интенсивности предназначен для формирования линейно изменяющегося во времени сигнала задания на скорость с определенным темпом. Структурная схема задатчика представлена на рис.20. Темп изменения выходного сигнала задатчика определяется уровнем ограничения Q нелинейного элемента (НЭ) и постоянной времени и интегратора (И).



Рис. 20. Структурная схема задатчика интенсивности

Определим параметры математической модели задатчика интенсивности в относительных единицах.

Темп задатчика:



Уровень ограничения нелинейного элемента (принимается):

Q=0,9

Постоянная времени интегрирующего звена ЗИ:



Коэффициент передачи в линейного зоне нелинейного элемента (принимается):

К_л=100
6.4.2 Конструктивный расчет задатчика интенсивности
Принципиальная схема задатчика интенсивности представлена на рис. 21. Нелинейный элемент реализуется на операционном усилителе DA 7. Ограничение выходного сигнала обеспечивается за счет включения в цепь обратной связи усилителя DA 7, стабилитронов VD 5 и

---

VD 6. Интегратор базируется на операционном усилителе DA 6. Емкость C7 в цепи в обратной связи операционного усилителя DA 6 определяет постоянную времени интегратора. Усилитель DA 5 предназначен для инвертирования сигнала, чтобы обеспечить отрицательную обратную связь, охватывающую нелинейный момент и интегратор (рис.24).



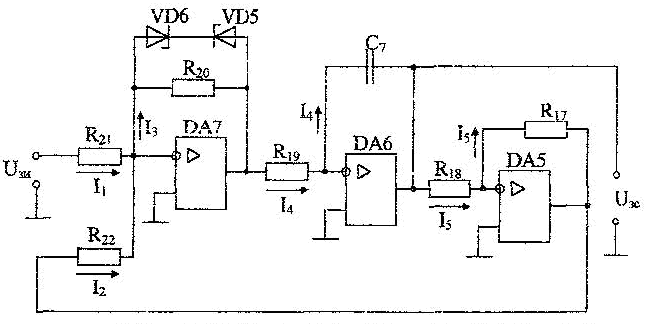
Рис21. Принципиальная схема задатчика интенсивности
На рис. 21 показана структурная схема для абсолютных величин токов опережений, соответствующая принципиальной схеме на рис. 20.



Рисунок 22.Структурная схема задатчика интенсивности для абсолютных величин
От структурной схемы задатчика интенсивности для абсолютных величин перейдем к структурной схеме для относительных величин (рис. 23).



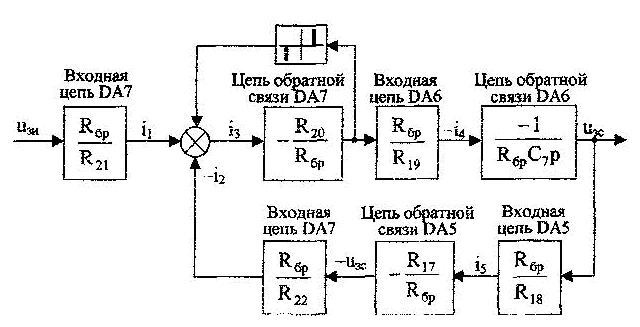
Рисунок 23.Структурная схема задатчика интенсивности для относительных величин
Из сравнения структурных схем задатчика интенсивности (см.рис.20 и 23): получим соотношения между параметрами математической модели и параметрами элементов принципиальной схемы задатчика.



Для обеспечения требуемого коэффициента передачи в линейной зоне нелинейного элемента должно выполняться условие:



Остальные сопротивления в схеме задатчика должны быть таковы, чтобы обеспечить единичные коэффициенты передачи. Для этого должно выполняться следующие условие:



7. ОСНОВЫ ТЕОРИИ СИСТЕМ ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ

Современные системы управления электроприводами строятся в большинстве случаев в виде многоконтурных систем подчиненного регулирования.

Рассмотрим теоретические положения, лежащие в основе синтеза структур, методов расчета и анализа свойств таких систем.

1. 
   Обобщенная схема многоконтурной системы подчиненного регулирования
   

Регулирующая часть | Силовая часть



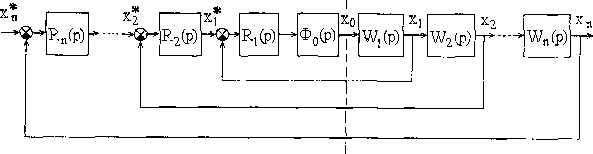
Рис. 24. Обобщенная структурная схема многоконтурной системы подчиненного регулирования

---

В основе построения систем подчиненного регулирования (СПР) лежит определенное структурное представление объекта регулирования, т.е. силовой части электропривода. Обобщенная структурная схема многоконтурной СПР представлена на рис. 24

Объект регулирования представлен в виде цепи последовательно соединенных звеньев направленного действия, передаточные функции которых обозначены как

i=1,……n

где n - количество звеньев модели объекта.

Разбиение модели объекта на звенья производится с таким расчетом, чтобы выходными величинами звеньев X₁, ... Х_n оказались физические величины, представляющие интерес с точки зрения регулирования и контроля (ток якоря, скорость вращения двигателя, угол поворота вала и т.д.).

Регулирующая часть системы починенного регулирования строится следующим образом.

На входе объекта регулирования (или же на выходе регулирующей части) устанавливается фильтр, ограничивающий полосу пропускания системы и обеспечивающий ее помехозащищенность. Передаточная функция этого фильтра обычно представляется в виде:



где - называется базовой или некомпенсируемой постоянной

времени системы подчиненного регулирования.

2.. Для каждой из регулируемых величин X₁,...X_n

предусматривается замкнутая САР с регулированием по отклонению. Каждая САР снабжена индивидуальным регулятором, передаточная функция которого обозначается как



Таким образом, количество регуляторов СПР равно количеству регулируемых величин объекта.

Для формирования сигнала обратной связи в каждой из САР предусматривается датчик соответствующей регулируемой величины, передаточную функцию которого обозначим как



В первом рассмотрении примем

=1

---

г.е. будем рассматривать систему с идеализированными датчиками, обеспечивающими безынерционные единичные обратные связи. Вопросы учета не идеальности датчиков будут служить предметом отдельного анализа, развивающего исходные принципиальные положения теории построения СПР.

3. 
   Подобно звеньям объекта регуляторы соединяются между собой последовательно, но в обратном порядке по отношению к порядку связи звеньев объекта. Сигналы задания для каждой из регулируемых величин Х₁...,X_n обозначены соответственно X₁^*……X_n^*. Каждый последующий (по мере возрастания номера) регулятор вырабатывает задание для предыдущего регулятора. Так как в структуре САР можно выделить ряд последовательно вложенных друг в друга контуров, то общее название этих систем - многоконтурныс системы подчиненного регулирования .
   

Вследствие последовательной подчиненности регуляторов и образуемых с их помощью локальных САР регулируемые величины не равноценны между собой. Основной (главной) из них является величина х„, процессу регулирования которой подчиняются процессы регулирования всех остальных величин.

7.2. Синтез регуляторов

Задача синтеза заключается в определении структуры и параметров контурных регуляторов. Синтез осуществляется по так называемой стандартной методике и заключается в следующем.

1. 
   Синтез регуляторов производится последовательно, начиная с регулятора внутреннего контура (т.е. регулятора величины X₁ ). После этого синтезируются регуляторы промежуточных контуров и, наконец, регулятор внешнего контура (регулятор величины X_n ).
   
2. 
   Каждый контурный регулятор выполняется в виде последовательного корректирующего устройства, обеспечивающего желаемые свойства данной локальной системы регулирования. Регулятор строится с таким расчетом, чтобы своим действием он:
   

1. 
   компенсировал действие (и прежде всего, проявление инерционности ) звена объекта, попадающего в данный контур ;
   
2. 
   обеспечивал астатизм системы по управляющему воздействию (т, е. равенство нулю установившейся ошибки САР при определенном типе управляющего воздействия).
   
3. 
   обеспечивал оптимизацию процессов регулирования по выбранному критерию.
   

Рассмотрим более конкретно методику синтеза регуляторов и свойства контуров системы подчиненного регулирования.

---

1. 
   Синтез регулятора первого контура и его свойства
   

Основой синтеза регулятора является расчетная схема САР величины X], изображенная на рис. 25


Здесь показана замкнутая система с регулированием по отклонению, элементами которой являются регулятор , фильтр и звено объекта. Передаточные функции этих элементов обозначаются соответственно как R₁(p), Ф₀(р) и W₁(p). Датчик регулируемой величины X₁ обеспечивает единичную обратную связь замкнутой САР.

В задаче синтеза регулятора заданной частью системы являются фильтр и звено объекта с передаточными функциями вида:







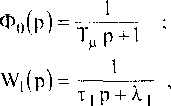
где Тμ - нскомпенсируемая постоянная времени, выбираемая

исходя из требуемого быстродействия и помехоустойчивости системы регулирования;

Т_1p - параметры звена объекта, попадающего в первый контур регулирования.

Последняя формула описывает при основных типа звеньев объекта регулирования.

Если τ₁>0 и λ₁=0 то звено является апериодическим. В этом случае параметры звена объекта определяются как

λ₁^-1 – коэффициент усиления

τ₁ λ₁^-1 - постоянная времени .
Если τ₁>0, λ₁=0, то т.е звено является интегрирующим

Если τ₁₌0, λ₁>0, то т.е звено является усилительным

К числу элементов САР с известными параметрами отнесем также датчик регулируемой величины. Напомним, что нами принято D_i(p) = 1, т.е. рассматривается система с безынерционной единичной

обратной связью по величине X_1.

Структура и параметры регулятора

---

Смотрите также файлы

• Курсовая работа по свиноводству Гибридизация в свиноводстве направление подготовки 36. 03. 02 Зоотехния.docx

• Выполнение второго раздела.docx

• Географический Москва.docx

• Особенности технологии непрерывной разливки высокоуглеродистой стали.docx

• Итоговая работа по русскому языку (5кл) Вариант 1 Укажите существительное с окончанием Е.doc