Добавлен: 22.11.2023
Просмотров: 69
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


| При ????????2 ≤ 350 для определения ???????? используем выражение ???????? = 0,002 ∙ ????????2 + 0,036 ∙ (???? − 9) = = 0,002 ∙ 248,5 + 0,036 ∙ (2,73 − 9) = 0,27 Тогда ???????????? = 1 + ???? ∙ (????с.т. − 5) ∙ ???????? = 1 + 0,06 ∙ (8 − 5) ∙ 0,27 = 1,05 Коэффициент неравномерности распределения нагрузки по ширине колеса 0 ???????????? = 1 + (???? ???????? − 1) ∙ ???????? где ????0???? – коэффициент неравномерности распределения нагрузки в ???? начальный период работы. Для определения ????0???? вычислим коэффициент ширины венца по диаметру ???? ???????????? = 0,5 ∙ ???????????? ∙ (????з.п. + 1) = 0,5 ∙ 0,315 ∙ (4 + 1) = 0,79 По значению ???????????? определим ????0???? ???? ????0???? ???? = 1,03 Тогда 0 ???????????? = 1 + (???? ???????? − 1) ∙ ???????? = 1 + (1,03 − 1) ∙ 0,27 = 1,01 Окончательно найдём коэффициент контактной нагрузки ???????? = ???????????? ∙ ???????????? ∙ ???????????? = 1,05 ∙ 1,01 ∙ 1,14 = 1,21 Выполняем проверочный расчёт зубьев на контактную прочность  ???? ???? ∙ ???? ∙ (???? + 1)3 σ???? =???? ∙ √???? 1 ф. = ???????? ????????2 ∙ ????ф.  = 9600 ∙ 1,21 ∙ 99,54 ∙ (3,92 + 1)3 = 513,29 [МПа] 160 √ 50 ∙ 3,92 Поскольку σ???? < σ????????( 515,45 [МПа] ), выполним расчет недогрузки по контактным напряжениям ∆σ = 100 ∙ σ???????? − σ???? = 100 ∙ 515,45 − 513,29 = 0,42 % < 15 % ???? σ???????? 515,45 | ||
| | 1303.303110.000.ПЗ | Лист |
| 14 | ||




| 2.4.2 Проверка изгибной прочности зубьев Напряжения изгиба в зубе шестерни σ = ???? ∙ 2000 ∙ ????1 ∙ ???????? ????1 ????1 ????????1 ∙ ????1 ∙ ???? где ????????1 – коэффициент формы зуба шестерни ???????? – коэффициент нагрузки при изгибе Напряжение изгиба в зубьях колеса σ????1 ∙ ????????1 ∙ ????????2 σ????2 = ????????2 ∙ ????????1 где ????????2 – коэффициент формы зуба колеса Коэффициент формы зуба при ???????? = 0 ???? = 3,47 + 13,2 ???????? ???????? Определяем коэффициент формы зуба ???? = 3,47 + 13,2 = 3,47 + 13,2 = 3,98 ????1 ????1 26 ???? = 3,47 + 13,2 = 3,47 + 13,2 = 3,60 ????2 ????2 102 Коэффициент нагрузки при изгибе ???????? = ???????????? ∙ ???????????? ∙ ???????????? Коэффициенты, входящие в эту формулу, имеют тот же физический смысл, что и коэффициенты в формуле для ????????. Для определения коэффициентов, входящих в эту формулу, используем следующие зависимости: ???????????? = 1 для прямозубых передач 0 ???????????? = 0,18 + 0,82 ∙ ???? ???????? = 0,18 + 0,82 ∙ 1,03 = 1,02 ???????????? = 1 + 1,5 ∙ (???????????? − 1) при ????????2 < 350 В результате получим ???????????? = 1 + 1,5 ∙ (???????????? − 1) = 1 + 1,5 ∙ (1,14 − 1) = 1,21 | ||
| | 1303.303110.000.ПЗ | Лист |
| 15 | ||







| Определяем коэффициент нагрузки при изгибе ???????? = ???????????? ∙ ???????????? ∙ ???????????? = 1 ∙ 1,02 ∙ 1,21 = 1,23 Тогда σ = ???? ∙ 2000 ∙ ????1 ∙ ???????? = ????1 ????1 ????????1 ∙ ????1 ∙ ???? = 3,98 ∙ 2000 ∙ 99,54 ∙ 1,23 = 113,16 [МПа] 53 ∙ 65 ∙ 2,5 σ????1 < σ????????1 (113,16 [МПа] < 191,04[МПа]) Напряжение изгиба в зубьях колеса ????????1 ∙ ????????1 ∙ ????????2  ????????2 = ????????2 ∙ ????????1 = = 113,16 ∙ 53 ∙ 3,60 = 108,5 [МПа] < σ (166,28 [МПа]) 50 ∙ 3,98 ????????2 | ||
| | 1303.303110.000.ПЗ | Лист |
| 16 | ||



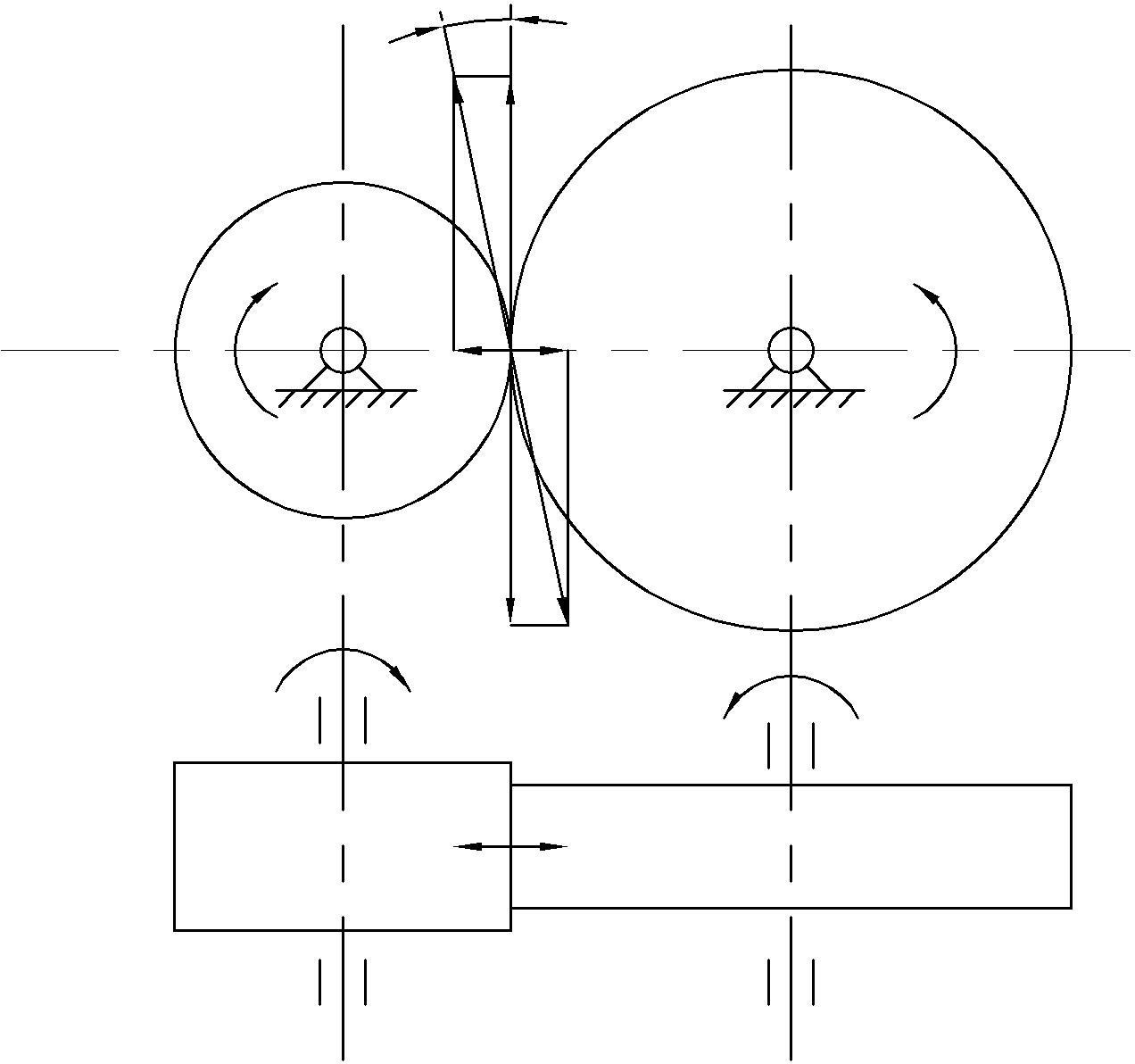
| 2.5 Силы в зацеплении Окружная сила ???? = 2000 ∙ ????1 = 2000 ∙ 99,54 = 3062,77[Н] = 3,06 [кН] ???? ????1 65 Распорная сила ???????? = ???????? ∙ tan ???????? = 3062,77 ∙ tan 20° = 1114,76[Н] = 1,11 [кН] где ???????? – угол зацепления, ???????? = 20° Полное усилие   ???????? = √????????2 + ????????2 = √3,062 + 1,112 = 3,26 [кН] Схема направления усилий ???????? ????????1 ????????1 ????1 ????2 ????????2 ????????1 ????1 ????????2 ???????? 2 ????2 ????????1 ????????2 | ||
| | 1303.303110.000.ПЗ | Лист |
| 17 | ||


| 3. Расчёт валов, подбор подшипников
 ???? = 3 ????1 ∙ 103 1 √ 0,2[????] где [????] = 12 … 25 [МПа], принимаем [????] = 15 [МПа] Тогда диаметр первого участка вала   ???? = 3 ????1 ∙ 103 = 3 99,54 ∙ 103 = 32,13 [мм] 1 √ 0,2[????] √ 0,2 ∙ 15 Полученный размер округлили до 32 [мм] из ряда нормальных линейных размеров по ГОСТ 6636 – 69. Остальные полученные значения диаметров также округляем в соответствии с ГОСТ 6636 – 69. ????2 = ????1 + 3 = 32 + 3 = 35 [мм] ????3 = ????7 = ????2 + 5 = 35 + 5 = 40 [мм] Предварительно выбираем подшипник 308 шариковый радиальный однорядный Геометрические характеристики подшипника ???? = 40 [мм], ???? = 90 [мм], ???? = 23 [мм], ????зп = 50 [мм] Участки 4-й и 6-й являются буртиками, предназначенными для осевой фиксации подшипников. Диаметр этих участков равен диаметру заплечиков для подшипников ????4 = ????6 = ????зп = 50 [мм] Длина первого участка вала ????1 = ????1 ∙ 1,5 = 32 ∙ 1,5 = 48 [мм] Полученный размер округлили до 50 [мм] из ряда нормальных линейных размеров по ГОСТ 6636 – 69.
  ???? = 3 ????2 ∙ 103 = 3 382 ∙ 103 = 50,31 ≈ 50 [мм] 1 √ 0,2[????] √ 0,2 ∙ 15 | ||
| | 1303.303110.000.ПЗ | Лист |
| 18 | ||





| ????2 = ????1 + 5 = 50 + 5 = 55 [мм] ????3 = ????7 = ????2 + 5 = 55 + 5 = 60 [мм] Предварительно выбираем подшипник 212 шариковый радиальный однорядный Геометрические характеристики подшипника ???? = 60 [мм], ???? = 110 [мм], ???? = 22 [мм], ????зп = 70 [мм] ????4 = ????3 + 5 = 60 + 5 = 65 [мм] ????5 = ????4 + 15 = 65 + 15 = 80 [мм] ????6 = ????зп = 70 [мм] Длина первого участка вала ????1 = ????1 ∙ 1,5 = 50 ∙ 1,5 = 75 [мм] Полученный размер округлили до 75 [мм] из ряда нормальных линейных размеров по ГОСТ 6636 – 69. 4. Подбор и расчёт шпонок Произведём расчёт шпонки для 4-го участка ведомого вала. Расчёт призматической шпонки выполняется как проверочный на смятие по формуле σ = 2000 ∙ ???? ≤ [σ ] см ???? ∙ (ℎ − ????1) ∙ ????р см где ???? – крутящий момент на участке вала со шпоночным пазом, [Н∙м] ???? – диаметр вала, ???? = 65[мм] ℎ – высота шпонки, ℎ = 11 [мм] ????1 – глубина паза на валу, ????1 = 7 [мм] ????р –рабочая длина шпонки Для шпонок со скругленными торцами ????р = ???? − ???? где ???? – длина шпонки, ???? = 50 [мм] ???? – ширина шпонки, ???? = 18 [мм] | ||
| | 1303.303110.000.ПЗ | Лист |
| 19 | ||