---

Таблица 2. Сравнительная характеристика планет земной группы и планет- гигантов.

Название группы	Объекты	Среднее расстояние от Солнца, а.е.	Средний радиус, радиусах Земли	Масса в массах Земли	Средняя плотность, г/см3	Период вращения	Число спутников	Наличие колец
Планеты земной группы
Планеты - гиганты

Практическая работа № 6.

«Определение основных характеристик звёзд».

1. 
   Разберите решение задачи. Параллакс звезды Арктур 0,085”. Определите расстояние до звезды.
   

Дано: Решение.

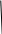
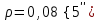Запишите формулу для определения расстояния: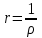

Найти: Подставьте значения:

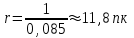
r - ? Выразите расстояние в световых годах:

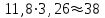
Ответ: расстояние до звезды Арктур 38 св. лет.

2. 
   Разберите решение задачи. Если бы по орбите Земли двигалась звезда с такой же массой, как у Солнца, каков бы был период её обращения?
   

---

Дано: Решение.

А = 1 а.е. Запишите формулу для определения массы двойных звёзд:

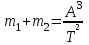
m 1 +m2 = 2M Преобразуйте формулу, выразив период обращения звёзд:

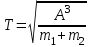
Найти: Подставьте значения:

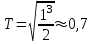
T - ? Ответ: период обращения звёзд был бы равен 0,7 лет.

2. 
   Разберите решение задачи. Во сколько раз Денеб больше Солнца?
   

Светимость и температуру поверхностизвезды выпишите из таблицы «Основные сведения о наиболее ярких звёздах, видимых в России».

Дано: Решение:

L = 16000 Запишите формулу для определения радиуса звезды:

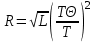
T = 9800 K Подставьте значения:

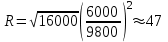
T = 6000 K

Найти: Ответ: Денеб больше Солнца в 47 раз.

R - ?

2. 
   Решите задачу. Параллакс звезды Денеб 0,005”. Определите расстояние до звезды.
   

2. 
   Решите задачу. У двойной звезды период обращения 100 лет. Большая полуось орбиты 40 а.е. Определите сумму масс двойной звезды.
   

2. 
   Решите задачу. Во сколько раз Капелла больше Солнца?
   

Практическая работа № 7

«Определение скорости движения звёзд в Галактике»

1. 
   Разберите решение задачи. Собственное движение звезды составляет 0,2” в год. Расстояние до неё 10 пк. Какова тангенциальная скорость звезды?
   

Дано: Решение.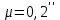

Запишите формулу для определения тангенциальной скорости: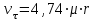

r = 10 пк Рассчитайте тангенциальную скорость звезды:

---

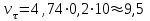
Найти: Ответ: тангенциальная скорость звезды 9,5 км/с.

2. 
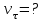
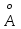   Разберите решение задачи. В спектре звезды из задачи № 1 смещение линии гелия 5876 составляет 0,6 . Определите лучевую скорость звезды.
   

Дано: Решение.

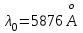Запишите формулу для определения лучевой скорости звезды при помощи

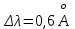спектрального анализа на основании эффекта Доплера: 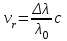, где

Найти: 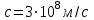- скорость света.

Рассчитайте лучевую скорость звезды: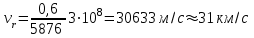

Ответ: лучевая скорость звезды 31 км/с.

2. 
   Разберите решение задачи. Определите пространственную скорость звезды, используя ответы к задачам №№ 1 и 2.
   

Дано: Решение:

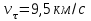Запишите теорему Пифагора для определения пространственной скорости звезды:

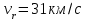
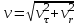. Рассчитайте пространственную скорость звезды:

Найти:

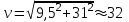
v - ? Ответ: пространственная скорость звезды 32 км/с.

2. 
   Решите задачу. Собственное движение звезды составляет 0,1” в год. Расстояние до неё 50 пк. Какова тангенциальная скорость звезды?
   
3. 
   Решите задачу. В спектре звезды из задачи № 4 смещение лабораторной длины волны 5000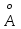 составляет 0,17 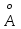. Определите лучевую скорость звезды.
   
4. 
   Решите задачу. Определите пространственную скорость звезды, используя ответы к задачам №№ 4 и 5.
   

---

Практическая работа №8

Задача 1. К каким светилам на широте Казани (φ = 5547′) относятся Сириус (α Большого Пса, δ = –1640′), Капелла (α Возничего, δ = +4558′) и Альдебаран (α Тельца, δ = +1627′)? Каково значение зенитного расстояния z этих звезд в моменты кульминаций?

Решение:

Светило будет считаться незаходящим, если его высота h ≥ 0, невосходящим, если h ≤ 0, восходящим и заходящим, если h (–90; +90). Известно, что высота h = 90° – φ + δ (δ < φ); h = 90° – δ + φ (δ > φ) в верхней кульминации и h = φ + δ – 90° в нижней кульминации.

Для Сириуса (δ < φ) h в верхней кульминации будет 90°–5547′+(–1640′) = 90°–5547′–1640′ = 1733′ > 0, h в нижней кульминации 5547′ + (–1640′) – 90°= h = 5547′ –1640′ – 90° = –5053′ < 0. Значит, светило восходящее и заходящее. Зенитное расстояние z = 90– h. В момент верхней кульминации z = 7227′, в момент нижней кульминации z = 14053′.

Аналогичные вычисления проводим для Капеллы и Альдебарана:

Капелла (δ < φ): h_вк = 8011′, h_нк = 1145′, z_вк = 949′, z_нк = 7815′, h > 0 незаходящее светило.

Альдебаран (δ < φ): h_вк = 5040′, h_нк = –1746′, z_вк = 3920′, z_нк = 10746′, h_вк > 0, h_нк < 0 восходящее и заходящее светило.

Задача 2. Долгота Новосибирска λ₂ = 5^h 31^m, долгота Москвы λ₁ = 2^h 30^m. Новосибирск находится в V часовом поясе.

1) Если днем в Новосибирске часы показывают 12:00, то что показывают в этот момент часы в Москве?

2) Если истинное солнечное время в Новосибирске 12:00, то каково оно в этот момент в Москве?

Решение:

1) Москва находится во втором часовом поясе, Новосибирск – в пятом. Разница во времени между городами составляет 5^h – 2^h = 3^h. Когда в Новосибирске полдень, в Москве 12^h – 3^h = 9^h (9 часов утра).

2) Разность любых двух времен (звездных, истинных солнечных, средних солнечных) равна разности долгот:

Т_λ2 – Т_λ1 = λ₂ – λ₁ = 3^h01^m.

Если истинное солнечное время в Новосибирске 12 часов, то в Москве оно 12^h – 3^h01^m = = 8^h59^m.

Ответ: 1) 9 часов утра; 2) 8^h59^m.

Задача 3. Когда по поясному времени Казани (λ = 3 ^h

---

Смотрите также файлы

• Федеральное государственное бюджетное образовательное учреждение высшего образования астраханский государственный медицинский университет.doc

• Реферат студента 2 курса 232 группы.docx

• Программа среднего профессионального образования 46. 02. 01 Документационное обеспечение управления и архивоведение Дисциплина Редактирование служебных документов Ручное практическое занятие.rtf

• Психология общения (ДО, СпДО, пнк, кп, пдо, доуа, ббл) Тест начат Четверг, 6 апреля 2023, 07 06.rtf

• Конспект Для обучения граждан Российской Федерации начальным знаниям в области обороны и их подготовки по основам военной службы.doc