Файл: Практическая работа Определение координат небесных объектов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 232
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
16m29 s, III часовой пояс) 22 июня произойдет кульминация Солнца, если уравнение времени в этот день равно +1m20s?
Решение:
В момент верхней кульминации Солнца истинное солнечное время Tи = 12h00 m. Местное среднее солнечное время отличается от истинного на величину уравнения времени Tм = Tи +η = 12h01 m20s. Для того чтобы найти поясное время, надо знать всемирное UT = Tм – = 12 h01m20 s – 3 h16m29 s = 8 h44m51 s и прибавить к нему номер пояса в часах Tп = UT + Nh = 8h44m51s + 3h = 11h44m51s.
Задачи для самостоятельного решения:
1. К каким светилам на широте Томска (φ = 5628′) относятся Альтаир (α Орла, δ = 848′), Полярная (α Большой Медведицы, δ = +8909′) и Ригель (β Ориона, δ = –814′)? Каково значение зенитного расстояния z этих звезд в моменты кульминаций?
2. Долгота Томска λ2 = 5h 39m, долгота Казани λ1 = 3h 16m. Томск находится в V часовом поясе.
1) Если днем в Томске часы показывают 13:00, то что показывают в этот момент часы в Казани?
2) Если истинное солнечное время в Томске 13:00, то каково оно в этот момент в Казани?
3. В Орле по часам, идущим по киевскому звездному времени, в 4h48m наблюдалась верхняя кульминация Капеллы (α = 5h10m). Какова разность долгот Орла и Киева?
4. Корабль, покинувший Сан-Франциско утром в среду 12 октября, прибыл во Владивосток ровно через 16 суток. Какого числа месяца и в какой день недели он прибыл?
Практическая работа №9
Задача 1. Как часто повторяются противостояния Марса, сидерический период S которого 1,9 года?
Решение:
Очевидно, нужно найти синодический период этой (верхней) планеты. Для этого воспользуемся формулой:
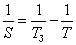 ,
,
где TЗ – сидерический период Земли, T – сидерический период Марса.
Тогда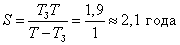 .
.
Ответ: S = 2,1 года.
Задача 2. Вычислите массу Юпитера
, зная, что один из его спутников (Ио) обращается вокруг планеты с периодом 1,77 сут. на расстоянии 422 000 км. (Сравните движение Ио вокруг Юпитера с движением Луны вокруг Земли. Период обращения Луны вокруг Земли 27,32 сут., среднее расстояние от Земли составляет 384 000 км).
Решение:
Для решения задачи необходимо воспользоваться третьим уточненным законом Кеплера:
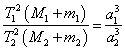 .
.
Принимая за первую пару Юпитер с Ио ( M1 – масса Юпитера, m1 – масса Ио, a1 – большая полуось орбиты Ио), а за вторую – Землю с Луной ( M2 – масса Земли, m2 – масса Луны, a2 – большая полуось орбиты Луны), а также пренебрегая массой спутников по сравнению с массой планет, получим:
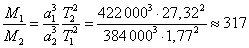 .
.
Ответ: M1 ≈ 317 M2.
Задача 3. Во сколько раз линейный радиус Солнца превышает радиус Земли, если угловой радиус Солнца равен 16′?
Решение:
Воспользуемся формулами п. 5.4, гл. 5 пособия.
Обозначим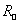 – радиус Солнца,
– радиус Солнца, 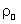 – видимый угловой радиус Солнца,
– видимый угловой радиус Солнца, 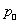 – параллакс Солнца,
– параллакс Солнца, 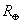 – радиус Земли. Тогда
– радиус Земли. Тогда
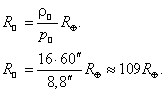
Ответ: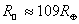 .
.
Задача 4. Флаг корабля привязан к мачте на высоте 30 метров над уровнем моря. На каком расстоянии l он будет виден на горизонте?
Решение:
Выполним рисунок (рис. 2).
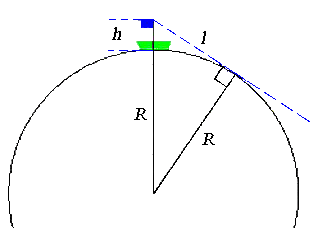
Рис. 2
Здесь h – высота флага над уровнем моря, R – радиус Земли. Ясно, что (R + h)2 = R2 + l2. Тогда
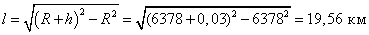 ,
,
если принять за R, например, средний экваториальный радиус Земли.
Ответ: l ≈ 19,56 км.
Задачи для самостоятельной работы
1. Наилучшая вечерняя видимость Венеры (наибольшее ее удаление к востоку от Солнца) была 5 февраля. Когда в следующий раз наступила видимость Венеры в тех же условиях?
2. Зная, что Сатурн совершает один оборот за 29,7 лет, найдите промежуток времени между его противостояниями.
3. Синодический период обращения одного из астероидов составляет 3 года. Каков звездный период его обращения около Солнца?
4. Найдите среднее суточное движение Меркурия по орбите (величину дуги орбиты, которую он проходит за земные сутки), если синодический период его обращения вокруг Солнца равняется 115,88 суткам.
5. Определите массу Урана в единицах массы Земли, сравнивая движение Луны вокруг Земли с движением спутника Урана – Титанией, обращающегося вокруг него с периодом 8,7 сут. на расстоянии 438 000 км. Период обращения Луны вокруг Земли 27,32 сут., среднее расстояние ее от Земли составляет 384 000 км.
6. Вычислите массу двойной звезды α Центавра, у которой период обращения компонентов вокруг общего центра масс T = 79 лет, а расстояние между ними 23,5 астрономических единицы (а. е.).
7. Чему равен горизонтальный параллакс Юпитера, когда он находится от Земли на расстоянии 6 а. е.? Горизонтальный параллакс Солнца p0 = 8,8″.
8. Наименьшее расстояние Венеры от Земли равно 40 млн. км. В этот момент ее угловой диаметр равен 32,4″. Определите линейный радиус этой планеты.
9. Определите дальность горизонта с маяка высотой 20 метров; с вершины пирамиды Хеопса (156 метров)?
10. Определите радиус Земли, если понижение горизонта с высоты 9 километров равняется 33′.
Практическая работа №10
Задача 1
Фокусное расстояние объектива телескопа составляет 900 мм, а фокусное расстояние используемого окуляра 25 мм. Определите увеличение телескопа.
Решение:
Увеличение телескопа определяется из соотношения: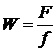 , где F – фокусное расстояние объектива, f – фокусное расстояние окуляра. Таким образом, увеличение телескопа составит
, где F – фокусное расстояние объектива, f – фокусное расстояние окуляра. Таким образом, увеличение телескопа составит 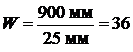 раз.
раз.
Ответ: 36 раз.
Задача 2
Переведите в часовую меру долготу Красноярска (l=92°52¢ в.д.).
Решение:
Исходя из соотношений часовой меры угла и градусной:
24 ч =360°, 1 ч =15°, 1 мин =15¢, 1 с = 15², а 1°=4 мин, и учитывая, что 92°52¢ = 92,87°, получим:
1 ч · 92,87°/15°= 6,19 ч = 6 ч 11 мин. в.д.
Ответ: 6 ч 11 мин. в.д.
Задача 3
Каково склонение звезды, если она кульминирует на высоте 63° в Красноярске, географическая широта которого равна 56° с.ш.?
Решение:
Используя соотношение, связывающие высоту светила в верхней кульминации, кульминирующего к югу от зенита, h, склонение светила δ и широту места наблюдения φ, h = δ + (90° – φ), получим:
δ = h + φ – 90° = 63° + 56° – 90° = 29°.
Ответ: 29°.
Задача 4
Когда в Гринвиче 10 ч 17 мин 14 с, в некотором пункте местное время равно 12 ч 43 мин 21 с. Какова долгота этого пункта?
Решение:
Местное время – это среднее солнечное время, а местное время Гринвича – это всемирное время. Воспользовавшись соотношением, связывающим среднее солнечное время Tm, всемирное время T0 и долготу l, выраженную в часовой мере: Tm = T0 +l, получим:
l = Tm – T0 = 12 ч 43 мин 21 с. – 10 ч 17 мин 14 с = 2ч 26 мин 07 с.
Ответ: 2ч 26 мин 07 с.
Задача 5
Через какой промежуток времени повторяются моменты максимальной удаленности Венеры от Земли, если ее звездный период равен 224,70 сут?
Решение:
Венера является нижней (внутренней) планетой. Конфигурация планеты, при которой происходит максимальная удаленность внутренней планеты от Земли, называется верхним соединением. А промежуток времени между последовательными одноименными конфигурациями планеты называется синодическим периодом S. Поэтому необходимо найти синодический период обращения Венеры. Воспользовавшись уравнением синодического движения для нижних (внутренних) планет
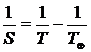 , где T – сидерический, или звездный период обращения планеты, TÅ – сидерический период обращения Земли (звездный год), равный 365,26 средних солнечных суток, найдем:
, где T – сидерический, или звездный период обращения планеты, TÅ – сидерический период обращения Земли (звездный год), равный 365,26 средних солнечных суток, найдем:
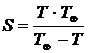
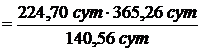 =583,91 сут.
=583,91 сут.
Ответ: 583,91 сут.
Практическая работа №11
Задача 1
Звездный период обращения Юпитера вокруг Солнца составляет около 12 лет. Каково среднее расстояние Юпитера от Солнца?
Решение:
Среднее расстояние планеты от Солнца равно большой полуоси эллиптической орбиты a. Из третьего закона Кеплера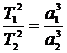 , сравнивая движение планеты с Землей, для которой приняв звездный период обращения T2 = 1 год, а большую полуось орбиты a2 = 1 а.е., получим простое выражение
, сравнивая движение планеты с Землей, для которой приняв звездный период обращения T2 = 1 год, а большую полуось орбиты a2 = 1 а.е., получим простое выражение 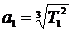 для определения среднего расстояния планеты от Солнца в астрономических единицах по известному звездному (сидерическому) периоду обращения, выраженному в годах. Подставив численные значения окончательно найдем:
для определения среднего расстояния планеты от Солнца в астрономических единицах по известному звездному (сидерическому) периоду обращения, выраженному в годах. Подставив численные значения окончательно найдем:
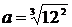 ≈ 5 а.е.
≈ 5 а.е.
Ответ: около 5 а.е.
Задача 2
Определите расстояние от Земли до Марса в момент его противостояния, когда его горизонтальный параллакс равен 18².
Решение:
Из формулы для определения геоцентрических расстояний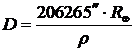 , где ρ – горизонтальный параллакс светила, RÅ = 6378 км – средний радиус Земли, определим расстояние до Марса в момент противостояния:
, где ρ – горизонтальный параллакс светила, RÅ = 6378 км – средний радиус Земли, определим расстояние до Марса в момент противостояния:
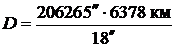 » 73×106 км. Разделив это значение на величину астрономической единицы, получим 73×106 км / 149,6×106 км » 0,5 а.е.
» 73×106 км. Разделив это значение на величину астрономической единицы, получим 73×106 км / 149,6×106 км » 0,5 а.е.
Ответ: 73×106 км » 0,5 а.е.
Задача 3
Горизонтальный параллакс Солнца равен 8,8². На каком расстоянии от Земли (в а.е.) находился Юпитер, когда его горизонтальный параллакс был 1,5²?
Решение:
В момент верхней кульминации Солнца истинное солнечное время Tи = 12h00 m. Местное среднее солнечное время отличается от истинного на величину уравнения времени Tм = Tи +η = 12h01 m20s. Для того чтобы найти поясное время, надо знать всемирное UT = Tм – = 12 h01m20 s – 3 h16m29 s = 8 h44m51 s и прибавить к нему номер пояса в часах Tп = UT + Nh = 8h44m51s + 3h = 11h44m51s.
Задачи для самостоятельного решения:
1. К каким светилам на широте Томска (φ = 5628′) относятся Альтаир (α Орла, δ = 848′), Полярная (α Большой Медведицы, δ = +8909′) и Ригель (β Ориона, δ = –814′)? Каково значение зенитного расстояния z этих звезд в моменты кульминаций?
2. Долгота Томска λ2 = 5h 39m, долгота Казани λ1 = 3h 16m. Томск находится в V часовом поясе.
1) Если днем в Томске часы показывают 13:00, то что показывают в этот момент часы в Казани?
2) Если истинное солнечное время в Томске 13:00, то каково оно в этот момент в Казани?
3. В Орле по часам, идущим по киевскому звездному времени, в 4h48m наблюдалась верхняя кульминация Капеллы (α = 5h10m). Какова разность долгот Орла и Киева?
4. Корабль, покинувший Сан-Франциско утром в среду 12 октября, прибыл во Владивосток ровно через 16 суток. Какого числа месяца и в какой день недели он прибыл?
Практическая работа №9
Задача 1. Как часто повторяются противостояния Марса, сидерический период S которого 1,9 года?
Решение:
Очевидно, нужно найти синодический период этой (верхней) планеты. Для этого воспользуемся формулой:
где TЗ – сидерический период Земли, T – сидерический период Марса.
Тогда
Ответ: S = 2,1 года.
Задача 2. Вычислите массу Юпитера
, зная, что один из его спутников (Ио) обращается вокруг планеты с периодом 1,77 сут. на расстоянии 422 000 км. (Сравните движение Ио вокруг Юпитера с движением Луны вокруг Земли. Период обращения Луны вокруг Земли 27,32 сут., среднее расстояние от Земли составляет 384 000 км).
Решение:
Для решения задачи необходимо воспользоваться третьим уточненным законом Кеплера:
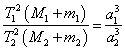 .
.Принимая за первую пару Юпитер с Ио ( M1 – масса Юпитера, m1 – масса Ио, a1 – большая полуось орбиты Ио), а за вторую – Землю с Луной ( M2 – масса Земли, m2 – масса Луны, a2 – большая полуось орбиты Луны), а также пренебрегая массой спутников по сравнению с массой планет, получим:
Ответ: M1 ≈ 317 M2.
Задача 3. Во сколько раз линейный радиус Солнца превышает радиус Земли, если угловой радиус Солнца равен 16′?
Решение:
Воспользуемся формулами п. 5.4, гл. 5 пособия.
Обозначим
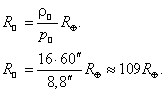
Ответ:
Задача 4. Флаг корабля привязан к мачте на высоте 30 метров над уровнем моря. На каком расстоянии l он будет виден на горизонте?
Решение:
Выполним рисунок (рис. 2).

Рис. 2
Здесь h – высота флага над уровнем моря, R – радиус Земли. Ясно, что (R + h)2 = R2 + l2. Тогда
если принять за R, например, средний экваториальный радиус Земли.
Ответ: l ≈ 19,56 км.
Задачи для самостоятельной работы
1. Наилучшая вечерняя видимость Венеры (наибольшее ее удаление к востоку от Солнца) была 5 февраля. Когда в следующий раз наступила видимость Венеры в тех же условиях?
2. Зная, что Сатурн совершает один оборот за 29,7 лет, найдите промежуток времени между его противостояниями.
3. Синодический период обращения одного из астероидов составляет 3 года. Каков звездный период его обращения около Солнца?
4. Найдите среднее суточное движение Меркурия по орбите (величину дуги орбиты, которую он проходит за земные сутки), если синодический период его обращения вокруг Солнца равняется 115,88 суткам.
5. Определите массу Урана в единицах массы Земли, сравнивая движение Луны вокруг Земли с движением спутника Урана – Титанией, обращающегося вокруг него с периодом 8,7 сут. на расстоянии 438 000 км. Период обращения Луны вокруг Земли 27,32 сут., среднее расстояние ее от Земли составляет 384 000 км.
6. Вычислите массу двойной звезды α Центавра, у которой период обращения компонентов вокруг общего центра масс T = 79 лет, а расстояние между ними 23,5 астрономических единицы (а. е.).
7. Чему равен горизонтальный параллакс Юпитера, когда он находится от Земли на расстоянии 6 а. е.? Горизонтальный параллакс Солнца p0 = 8,8″.
8. Наименьшее расстояние Венеры от Земли равно 40 млн. км. В этот момент ее угловой диаметр равен 32,4″. Определите линейный радиус этой планеты.
9. Определите дальность горизонта с маяка высотой 20 метров; с вершины пирамиды Хеопса (156 метров)?
10. Определите радиус Земли, если понижение горизонта с высоты 9 километров равняется 33′.
Практическая работа №10
Задача 1
Фокусное расстояние объектива телескопа составляет 900 мм, а фокусное расстояние используемого окуляра 25 мм. Определите увеличение телескопа.
Решение:
Увеличение телескопа определяется из соотношения:
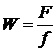 , где F – фокусное расстояние объектива, f – фокусное расстояние окуляра. Таким образом, увеличение телескопа составит
, где F – фокусное расстояние объектива, f – фокусное расстояние окуляра. Таким образом, увеличение телескопа составит 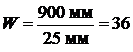 раз.
раз.Ответ: 36 раз.
Задача 2
Переведите в часовую меру долготу Красноярска (l=92°52¢ в.д.).
Решение:
Исходя из соотношений часовой меры угла и градусной:
24 ч =360°, 1 ч =15°, 1 мин =15¢, 1 с = 15², а 1°=4 мин, и учитывая, что 92°52¢ = 92,87°, получим:
1 ч · 92,87°/15°= 6,19 ч = 6 ч 11 мин. в.д.
Ответ: 6 ч 11 мин. в.д.
Задача 3
Каково склонение звезды, если она кульминирует на высоте 63° в Красноярске, географическая широта которого равна 56° с.ш.?
Решение:
Используя соотношение, связывающие высоту светила в верхней кульминации, кульминирующего к югу от зенита, h, склонение светила δ и широту места наблюдения φ, h = δ + (90° – φ), получим:
δ = h + φ – 90° = 63° + 56° – 90° = 29°.
Ответ: 29°.
Задача 4
Когда в Гринвиче 10 ч 17 мин 14 с, в некотором пункте местное время равно 12 ч 43 мин 21 с. Какова долгота этого пункта?
Решение:
Местное время – это среднее солнечное время, а местное время Гринвича – это всемирное время. Воспользовавшись соотношением, связывающим среднее солнечное время Tm, всемирное время T0 и долготу l, выраженную в часовой мере: Tm = T0 +l, получим:
l = Tm – T0 = 12 ч 43 мин 21 с. – 10 ч 17 мин 14 с = 2ч 26 мин 07 с.
Ответ: 2ч 26 мин 07 с.
Задача 5
Через какой промежуток времени повторяются моменты максимальной удаленности Венеры от Земли, если ее звездный период равен 224,70 сут?
Решение:
Венера является нижней (внутренней) планетой. Конфигурация планеты, при которой происходит максимальная удаленность внутренней планеты от Земли, называется верхним соединением. А промежуток времени между последовательными одноименными конфигурациями планеты называется синодическим периодом S. Поэтому необходимо найти синодический период обращения Венеры. Воспользовавшись уравнением синодического движения для нижних (внутренних) планет
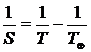 , где T – сидерический, или звездный период обращения планеты, TÅ – сидерический период обращения Земли (звездный год), равный 365,26 средних солнечных суток, найдем:
, где T – сидерический, или звездный период обращения планеты, TÅ – сидерический период обращения Земли (звездный год), равный 365,26 средних солнечных суток, найдем: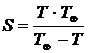
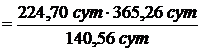 =583,91 сут.
=583,91 сут.Ответ: 583,91 сут.
Практическая работа №11
Задача 1
Звездный период обращения Юпитера вокруг Солнца составляет около 12 лет. Каково среднее расстояние Юпитера от Солнца?
Решение:
Среднее расстояние планеты от Солнца равно большой полуоси эллиптической орбиты a. Из третьего закона Кеплера
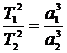 , сравнивая движение планеты с Землей, для которой приняв звездный период обращения T2 = 1 год, а большую полуось орбиты a2 = 1 а.е., получим простое выражение
, сравнивая движение планеты с Землей, для которой приняв звездный период обращения T2 = 1 год, а большую полуось орбиты a2 = 1 а.е., получим простое выражение Ответ: около 5 а.е.
Задача 2
Определите расстояние от Земли до Марса в момент его противостояния, когда его горизонтальный параллакс равен 18².
Решение:
Из формулы для определения геоцентрических расстояний
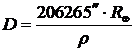 , где ρ – горизонтальный параллакс светила, RÅ = 6378 км – средний радиус Земли, определим расстояние до Марса в момент противостояния:
, где ρ – горизонтальный параллакс светила, RÅ = 6378 км – средний радиус Земли, определим расстояние до Марса в момент противостояния:Ответ: 73×106 км » 0,5 а.е.
Задача 3
Горизонтальный параллакс Солнца равен 8,8². На каком расстоянии от Земли (в а.е.) находился Юпитер, когда его горизонтальный параллакс был 1,5²?