Решение:

Из формулы   видно, что геоцентрическое расстояние одного светила D1 обратно пропорционально его горизонтальному параллаксу ρ1, т.е. 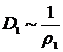  . Аналогичную пропорциональность можно записать для другого светила у которого известны расстояние D2 и горизонтальный параллакс ρ2:  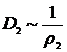 . Разделив одно соотношение на другое, получим  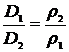 . Таким образом, зная из условия задачи, что горизонтальный параллакс Солнца равен 8,8², при этом оно находится на 1 а.е. от Земли, можно легко найти расстояние до Юпитера по известному горизонтальному параллаксу планеты в этот момент:

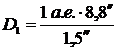 =5,9 а.е.

Ответ: 5,9 а.е.

Задача 4

Определите линейный радиус Марса, если известно, что во время великого противостояния его угловой радиус составляет 12,5², а горизонтальный параллакс равен 23,4².

Решение:

Линейный радиус светил R можно определить из соотношения 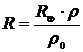  , r – угловой радиус светила, r0 – его горизонтальный параллакс, RÅ – радиус Земли, равный 6378 км. Подставив значения из условия задачи, получим:  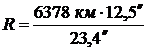 = 3407 км.

Ответ: 3407 км.

Задача 5

Во сколько раз масса Плутона меньше массы Земли, если известно, что расстояние до его спутника Харона 19,64×103 км, а период обращения спутника равен 6,4 сут. Расстояние Луны от Земли составляет 3,84×105 км, а период обращения 27,3 сут.

Решение:

Для определения масс небесных тел нужно воспользоваться третьим обобщенным законом Кеплера: 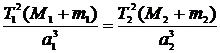  . Так как массы планет M1 и М2 значительно меньше, чем массы их спутников m1 и m2, то массами спутников можно пренебречь. Тогда этот закон Кеплера можно переписать в следующем виде: 

---

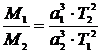 , где а1 – большая полуось орбиты спутника первой планеты с массой M1, T1 – период обращения спутника первой планеты, а2 – большая полуось орбиты спутника второй планеты с массой M2, T2 – период обращения спутника второй планеты.

Подставив соответствующие значения из условия задачи, получим:

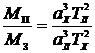
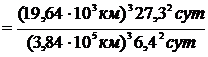   = 0,0024.

Ответ: в 0,0024 раза.

Практическая работа №12

Задача 1

Космический зонд «Гюйгенс» 14 января 2005 года совершил посадку на спутник Сатурна Титан. Во время снижения он передал на Землю фотографию поверхности этого небесного тела, на которой видны образования похожие на реки и моря. Оцените среднюю температуру на поверхности Титана. Как Вы думаете, из какой жидкости могут состоять реки и моря на Титане?

Указание: Расстояние от Солнца до Сатурна составляет 9,54 а.е. Отражательную способность Земли и Титана считать одинаковой, а среднюю температуру на поверхности Земли равной 16°С.

Решение:

Энергии, получаемые Землей и Титаном обратно пропорциональны квадратам их расстояний от Солнца r. Часть энергии отражается, часть поглощается и идет на нагрев поверхности. Считая, что отражательная способность этих небесных тел одинакова, то процент энергии идущий на нагрев этих тел будет одинаков. Оценим температуру поверхности Титана в приближении абсолютно черного тела, т.е. когда количество поглощаемой энергии равно количеству излучаемой энергии нагретым телом. Согласно закону Стефана-Больцмана энергия, излучаемая единицей поверхности в единицу времени пропорциональна четвертой степени абсолютной температуры тела 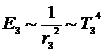  . Таким образом, для энергии, поглощаемой Землей можем записать   , где rз – расстояние от Солнца до Земли, Tз –средняя температура на поверхности Земли, а Титаном –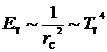 

---

 , где rc – расстояние от Солнца до Сатурна с его спутником Титаном, TT –средняя температура на поверхности Титана. Взяв отношение, получим: 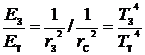  , отсюда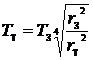 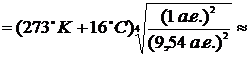    94°K = (94°K – 273°K) = –179°С. При такой низкой температуре моря на Титане могут состоять из жидкого газа, например, метана или этана.

Ответ: Из жидкого газа, например, метана или этана, так как температура на Титане –179°С.

Задача 2

Какую видимую звездную величину имеет Солнце, наблюдаемое с ближайшей звезды? Расстояние до нее составляет около 270 000 а.е.

Решение:

Воспользуемся формулой Погсона: 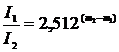  , где I1 и I2 – яркости источников, m1 и m2 – их звездные величины соответственно. Так как яркость обратно пропорциональна квадрату расстояния до источника  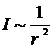 , то можно записать  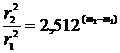 . Логарифмируя это выражение, получим  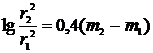 . Известно, что видимая звездная величина Солнца с Земли (с расстояния r1 = 1 а.е.) m1 = –26,8. Требуется найти видимую звездную величину Солнца m2 с расстояния r2 = 270 000 а.е. Подставив эти значения в выражение, получим:

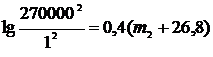 , отсюда   ≈ 0,4m.

Ответ: 0,4m.

 

Задача 3

Годичный параллакс Сириуса (a Большого Пса) составляет 0,377². Чему равно расстояние до этой звезды в парсеках и световых годах?

Решение:

Расстояния до звезд в парсеках определяется из соотношения 

---

 , где π – годичный параллакс звезды. Поэтому 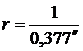  = 2,65 пк. Так 1 пк = 3,26 св. г., то расстояние до Сириуса в световых годах будет составлять 2,65 пк · 3,26 св. г. = 8,64 св. г.

Ответ: 2,63 пк или 8,64 св. г.

 

Задача 4

Видимая звездная величина звезды Сириуса равна –1,46m, а расстояние составляет 2,65 пк. Определите абсолютную звездную величину этой звезды.

Решение:

Абсолютная звездная величина M связана с видимой звездной величиной m и расстоянием до звезды r в парсеках следующим соотношением: 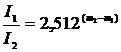  . Эту формулу можно вывести из формулы Погсона   , зная, что абсолютная звездная величина – это звездная величина, которую имела бы звезда, если бы она находилась на стандартном расстоянии r0 = 10 пк. Для этого перепишем формулу Погсона в виде  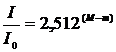 , где I – яркость звезды на Земле c расстояния r, а I0 – яркость с расстояния r0 = 10 пк. Так как видимая яркость звезды изменятся обратно пропорционально квадрату расстояния до нее, т.е.  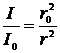 , то   . Логарифмируя, получаем:   или   или   .

Подставив в это соотношение значения из условия задачи, получим:

 = 1,42m.

Ответ: M = 1,42m.

 

Задача 5

Во сколько раз звезда Арктур (a Волопаса) больше Солнца, если светимость Арктура в 100 раз больше солнечной, а температура 4500° К?

Решение:

Светимость звезды L – полную энергию излучаемую звездой в единицу времени можно определить как 

---

 , где S – площадь поверхности звезды, ε – энергия, излучаемая звездой с единицы площади поверхности, которая определяется законом Стефана-Больцмана   , где σ – постоянная Стефана-Больцмана, T – абсолютная температура поверхности звезды. Таким образом, можно записать:   , где R – радиус звезды. Для Солнца можно записать аналогичное выражение:   , где Lс –светимость Солнца, Rс – радиус Солнца, Tс – температура поверхности Солнца. Разделив одно выражение на другое, получим:



Или можно записать это соотношение таким образом: 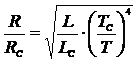  . Приняв для Солнца Rс=1 и Lс=1, получим  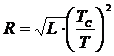 . Подставив значения из условия задачи, найдем радиус звезды в радиусах Солнца (или во сколько раз звезда больше или меньше Солнца):

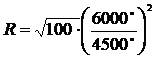 ≈ 18 раз.

Ответ: в 18 раз.

Практическая работа №13

Задача 1

В спиральной галактике в созвездии Треугольника наблюдаются цефеиды с периодом 13 дней, а их видимая звездная величина 19,6m. Определите расстояние до галактики в световых годах.

Указание: Абсолютная звездная величина цефеиды с указанным периодом равна M = – 4,6m.

Решение:

Из соотношения   , связывающего абсолютную звездную величину M с видимой звездной величиной m и расстоянием до звезды r, выраженному в парсеках, получим:   = 

---

Смотрите также файлы

• Федеральное государственное бюджетное образовательное учреждение высшего образования астраханский государственный медицинский университет.doc

• Реферат студента 2 курса 232 группы.docx

• Программа среднего профессионального образования 46. 02. 01 Документационное обеспечение управления и архивоведение Дисциплина Редактирование служебных документов Ручное практическое занятие.rtf

• Психология общения (ДО, СпДО, пнк, кп, пдо, доуа, ббл) Тест начат Четверг, 6 апреля 2023, 07 06.rtf

• Конспект Для обучения граждан Российской Федерации начальным знаниям в области обороны и их подготовки по основам военной службы.doc