ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 193
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
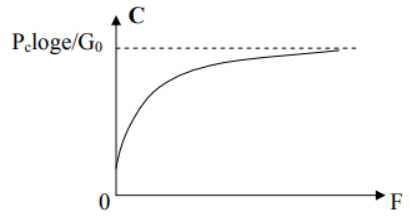
с*log e/G0
Билет 11.
1. Частотный детектор. Временные диаграммы и спектры сигналов на входе и выходе. СХД.
Назначение частотного детектора (ЧД) состоит в том, чтобы из ВЧ модулированного ЧМ сигнала получить НЧ модулирующий сигнал.
ЧД преобразует ЧМ сигнал в амплитудно - частотно модулированный (АЧМ), который детектируется с помощью амплитудного детектора. Наиболее распространенная схема ЧД - ЧД с расстроенными контурами. Его принципиальная схема имеет вид:
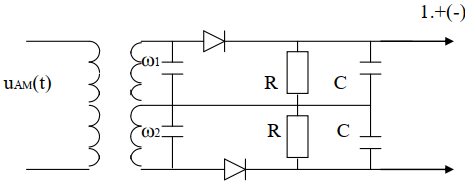
Контура расстроены относительно средней частоты ЧМ сигнала ω0. Например: ω1> ω0, ω2< ω0.
Если частота ЧМ сигнала больше ω0 [ωчм(t) > ω0], то она ближе к ω1, чем к ω2, т.е. напряжение (его амплитуда) на верхнем контуре (на входе Д1) больше чем напряжение на выходе нижнего контура (на входе Д2). Напряжение в точке 1 будет больше чем в точке 2.
Если [ωчм(t) < ω0], т.е. ближе к ω2 то, так же рассуждая, получим, что напряжение в точке 2 будет больше чем в точке 1. Полярность напряжения на выходе Uнч(t) меняется на противоположную. Основная характеристика - статическая характеристика детектора. Это зависимость постоянной составляющей тока в нагрузке детектора I0 от частоты входного сигнала.
I0 = φ(ω) I0 = φ(f)
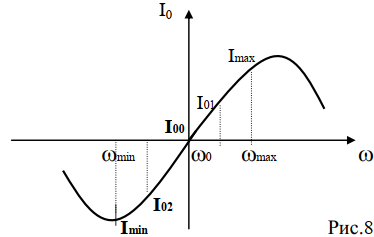
Стандартный вид СХД следующий:
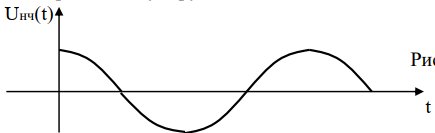
Временная диаграмма модулирующего сигнала (вход) имеет вид:
Временная диаграмма соответствующего ЧМ сигнала (выход) принимает вид:
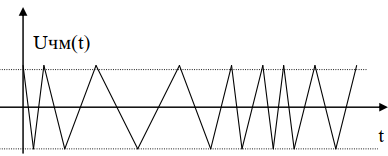
Как видно там, где модулирующий сигнал больше, там и
частота ЧМ сигнала больше, а период колебаний меньше.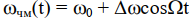
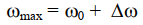
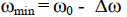 .
.
Амплитуда при ЧМ постоянна, меняется только частота.
Для получения спектра ЧМ сигнала разложим Uчм(t) в ряд Фурье.
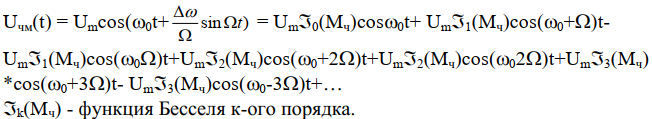
Вид спектра зависит от Мч

При Мч<<1 спектр ЧМ сигнала похож на спектр АМ сигнала (несущая, 2 боковых), но для ЧМ этот спектр приближенный. Все остальные боковые
тоже есть, но они очень малы.

Полоса частот сигнала ЧМ.
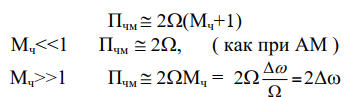
Ширина спектра при Мч>>1 не зависит от модулирующей частоты. Это
широкополосный сигнал.
2. Оптимальный приемник двоичных сигналов на СФ.
У Артёма
Билет 12
1.Теорема Котельникова.
2. Согласованный фильтр.
Оптимальный фильтр - это фильтр, обеспечивающий на выходе максимальное отношение мощности сигнала к мощности шума. Если помеха, поражающая сигнал, является белым шумом, то оптимальный фильтр называется - согласованным фильтром (СФ). Таким образом, если на вход СФ поступает сигнал uc(t) в сумме с белым шумом x(t):
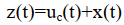
то на выходе СФ получим максимальное отношение мощности сигнала к мощности шума. Определим, какими должны быть характеристики СФ. Напряжение на выходе линейного фильтра с импульсной реакцией g(t) имеет вид:
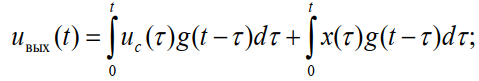
Первое слагаемое – напряжение полезного сигнала, второе – напряжение помехи. Дисперсия помехи равна:
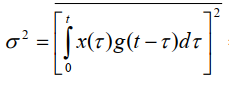
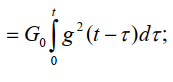
Отношение мощности сигнала к дисперсии шума на выходе СФ равно:
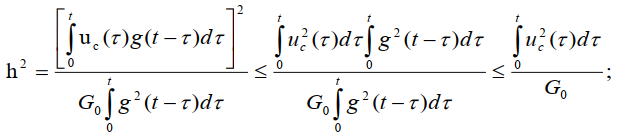
Это равенство достигается только при условии, что
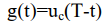
Это означает, что название фильтра "согласованный" определяется тем, что его характеристики согласованы с характеристиками сигнала u
с(t):
- импульсная реакция g(t) согласованного фильтра совпадает с зеркальным отображением сигнала:

Для импульса несимметричной формы, заданного, например, выражением:
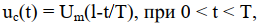
импульсная реакция фильтра, согласованного с ним, равна:
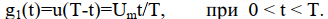
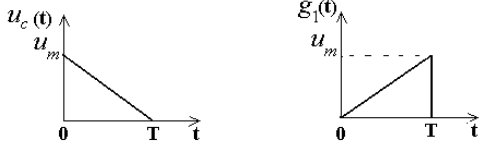
Соответствующий треугольный сигнальный импульс и импульсная реакция согласованного с ним фильтра имеют вид:
Определим частотную характеристику СФ, как преобразование Фурье от g(t):
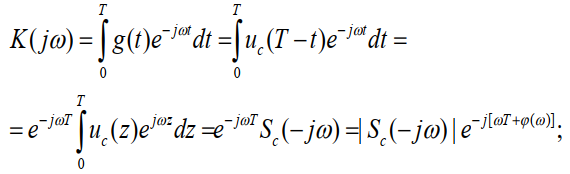
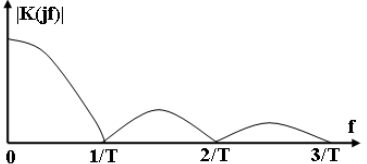
Таким образом, амплитудно-частотная характеристика (АЧХ) согласованного фильтра |К(jω)| с точностью до постоянного множителя A совпадает с амплитудным спектром сигнала |S(jω)|:
|К(jω)|=A|S(jω)|
- фазо-частотная характеристика (ФЧХ) согласованного фильтра
противоположна по знаку ФЧХ сигнала:
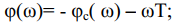
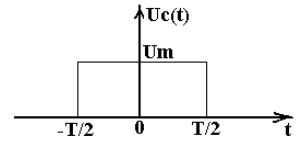
Рассмотрим характеристики фильтра, согласованного с одиночным прямоугольным импульсом (рис.3.2). Такой импульс описывается выражением: u(t)=Um, при -0,5Т < t < 0,5Т ;
где Um, T - амплитуда и длительность импульса, соответственно.
Спектр этого импульса равен: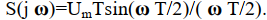
Следовательно, АЧХ фильтра, согласованного с прямоугольным импульсом равна:
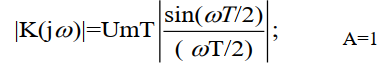
АЧХ фильтра, согласованного с прямоугольным
импульсом длительностью Т:
Согласованный фильтр обеспечивает на выходе максимальное отношение мощности сигнала к мощности шума (с/ш), если помеха является белым шумом. Т.е. отношению энергии посылки сигнала к
спектральной плотности энергии белого шума: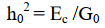
Билет 13
1.Дискретизация непрерывных сигналов.
Непрерывные сигналы описывают непрерывную функцию времени. Они изменяются плавно, без резких скачков.
Дискретизация – это преобразование непрерывного сигнала в последовательность чисел (отсчетов) соответствующих определенным моментам времени kt.
Временные диаграммы непрерывного сигнала x(t) и дискретизированного xд(t) имеют вид:
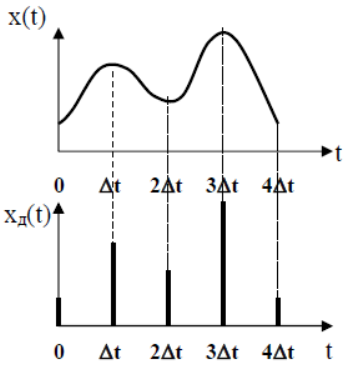
Для дискретизации сигналов применяют теорему Котельникова.
Дальше про теорему Котельникова
2. Энтропия. Способы ее увеличения.
Энтропия (H) - это среднее количество информации, приходящееся на одно сообщение, символ, слово источника информации.
Энтропия характеризует также среднюю неопределенность ситуации. Чем больше энтропия, тем больше неопределенность ситуации и , следовательно, тем больше информации мы получаем, когда принимаем некоторое сообщение, которое устраняет неопределенность.
Энтропия дискретного источника независимых символов равна:
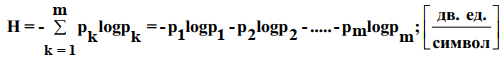
pk - вероятность к-го символа.
m - основание кода - общее количество разных символов.
Энтропия дискретного источника независимых сообщений максимальна, если все сообщения равновероятны т.е.:
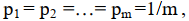
так как сумма всех вероятностей равна 1.
Максимальное значение энтропии:
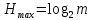
Энтропия двоичного источника независимых сообщений может быть определена по формуле:
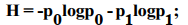

Билет 11.
1. Частотный детектор. Временные диаграммы и спектры сигналов на входе и выходе. СХД.
Назначение частотного детектора (ЧД) состоит в том, чтобы из ВЧ модулированного ЧМ сигнала получить НЧ модулирующий сигнал.
ЧД преобразует ЧМ сигнал в амплитудно - частотно модулированный (АЧМ), который детектируется с помощью амплитудного детектора. Наиболее распространенная схема ЧД - ЧД с расстроенными контурами. Его принципиальная схема имеет вид:

Контура расстроены относительно средней частоты ЧМ сигнала ω0. Например: ω1> ω0, ω2< ω0.
Если частота ЧМ сигнала больше ω0 [ωчм(t) > ω0], то она ближе к ω1, чем к ω2, т.е. напряжение (его амплитуда) на верхнем контуре (на входе Д1) больше чем напряжение на выходе нижнего контура (на входе Д2). Напряжение в точке 1 будет больше чем в точке 2.
Если [ωчм(t) < ω0], т.е. ближе к ω2 то, так же рассуждая, получим, что напряжение в точке 2 будет больше чем в точке 1. Полярность напряжения на выходе Uнч(t) меняется на противоположную. Основная характеристика - статическая характеристика детектора. Это зависимость постоянной составляющей тока в нагрузке детектора I0 от частоты входного сигнала.
I0 = φ(ω) I0 = φ(f)
Стандартный вид СХД следующий:

Временная диаграмма модулирующего сигнала (вход) имеет вид:

Временная диаграмма соответствующего ЧМ сигнала (выход) принимает вид:

Как видно там, где модулирующий сигнал больше, там и
частота ЧМ сигнала больше, а период колебаний меньше.
Амплитуда при ЧМ постоянна, меняется только частота.
Для получения спектра ЧМ сигнала разложим Uчм(t) в ряд Фурье.
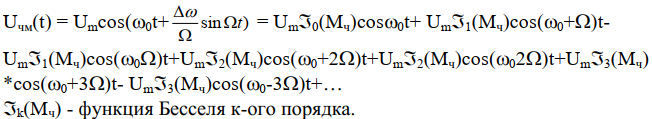
Вид спектра зависит от Мч

При Мч<<1 спектр ЧМ сигнала похож на спектр АМ сигнала (несущая, 2 боковых), но для ЧМ этот спектр приближенный. Все остальные боковые
тоже есть, но они очень малы.

Полоса частот сигнала ЧМ.
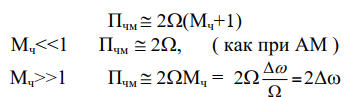
Ширина спектра при Мч>>1 не зависит от модулирующей частоты. Это
широкополосный сигнал.
2. Оптимальный приемник двоичных сигналов на СФ.
У Артёма
Билет 12
1.Теорема Котельникова.
2. Согласованный фильтр.
Оптимальный фильтр - это фильтр, обеспечивающий на выходе максимальное отношение мощности сигнала к мощности шума. Если помеха, поражающая сигнал, является белым шумом, то оптимальный фильтр называется - согласованным фильтром (СФ). Таким образом, если на вход СФ поступает сигнал uc(t) в сумме с белым шумом x(t):
то на выходе СФ получим максимальное отношение мощности сигнала к мощности шума. Определим, какими должны быть характеристики СФ. Напряжение на выходе линейного фильтра с импульсной реакцией g(t) имеет вид:
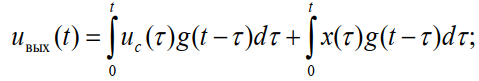
Первое слагаемое – напряжение полезного сигнала, второе – напряжение помехи. Дисперсия помехи равна:
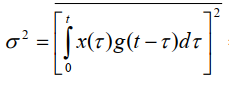
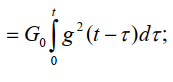
Отношение мощности сигнала к дисперсии шума на выходе СФ равно:
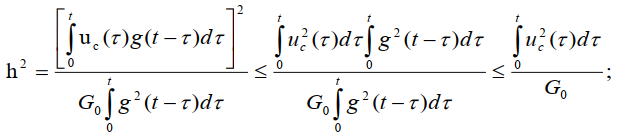
Это равенство достигается только при условии, что
Это означает, что название фильтра "согласованный" определяется тем, что его характеристики согласованы с характеристиками сигнала u
с(t):
- импульсная реакция g(t) согласованного фильтра совпадает с зеркальным отображением сигнала:
Для импульса несимметричной формы, заданного, например, выражением:
импульсная реакция фильтра, согласованного с ним, равна:
Соответствующий треугольный сигнальный импульс и импульсная реакция согласованного с ним фильтра имеют вид:

Определим частотную характеристику СФ, как преобразование Фурье от g(t):
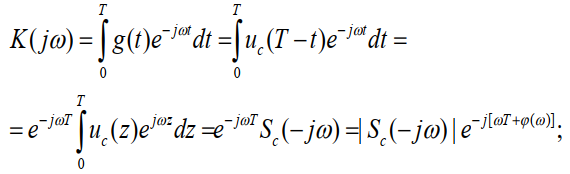
Таким образом, амплитудно-частотная характеристика (АЧХ) согласованного фильтра |К(jω)| с точностью до постоянного множителя A совпадает с амплитудным спектром сигнала |S(jω)|:
|К(jω)|=A|S(jω)|
- фазо-частотная характеристика (ФЧХ) согласованного фильтра
противоположна по знаку ФЧХ сигнала:
Рассмотрим характеристики фильтра, согласованного с одиночным прямоугольным импульсом (рис.3.2). Такой импульс описывается выражением: u(t)=Um, при -0,5Т < t < 0,5Т ;
где Um, T - амплитуда и длительность импульса, соответственно.

Спектр этого импульса равен:
Следовательно, АЧХ фильтра, согласованного с прямоугольным импульсом равна:
АЧХ фильтра, согласованного с прямоугольным
импульсом длительностью Т:

Согласованный фильтр обеспечивает на выходе максимальное отношение мощности сигнала к мощности шума (с/ш), если помеха является белым шумом. Т.е. отношению энергии посылки сигнала к
спектральной плотности энергии белого шума:
Билет 13
1.Дискретизация непрерывных сигналов.
Непрерывные сигналы описывают непрерывную функцию времени. Они изменяются плавно, без резких скачков.
Дискретизация – это преобразование непрерывного сигнала в последовательность чисел (отсчетов) соответствующих определенным моментам времени kt.
Временные диаграммы непрерывного сигнала x(t) и дискретизированного xд(t) имеют вид:

Для дискретизации сигналов применяют теорему Котельникова.
Дальше про теорему Котельникова
2. Энтропия. Способы ее увеличения.
Энтропия (H) - это среднее количество информации, приходящееся на одно сообщение, символ, слово источника информации.
Энтропия характеризует также среднюю неопределенность ситуации. Чем больше энтропия, тем больше неопределенность ситуации и , следовательно, тем больше информации мы получаем, когда принимаем некоторое сообщение, которое устраняет неопределенность.
Энтропия дискретного источника независимых символов равна:
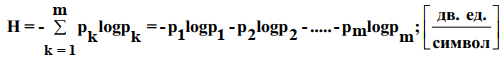
pk - вероятность к-го символа.
m - основание кода - общее количество разных символов.
Энтропия дискретного источника независимых сообщений максимальна, если все сообщения равновероятны т.е.:
так как сумма всех вероятностей равна 1.
Максимальное значение энтропии:
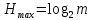
Энтропия двоичного источника независимых сообщений может быть определена по формуле: