ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 194
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
цифро-аналоговым преобразователем (ЦАП).
Билет 20.
1.Амплитудный модулятор. Расчет СМХ (метод угла отсечки) (Амплитудный модулятор в 38)
СМХ – это зависимость амплитуды 1-ой гармоники выходного тока I1 модулятора от напряжения смещения E при амплитуде вч несущей Um=const и амплитуде нч модулирующего сигнала Vm = 0.
Расчет СМХ методом угла отсечки.
1.Аппроксимируем ВАХ отрезками прямых.
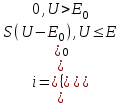S<0;
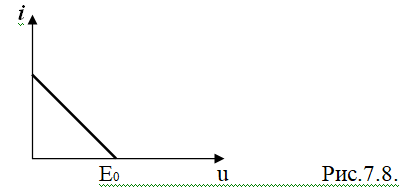
2. Определяем пределы изменения смещения E.
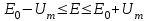
Um – амплитуда несущей.
3. Задаёмся напряжением смещения Е/.
4. Определяем угол отсечки:
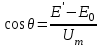
5. Определяем амплитуду первой гармоники:
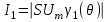, где 1()-коэффициент Берга (см. учебник[1])
6. Возвращаемся в пункт 3 и т.д.
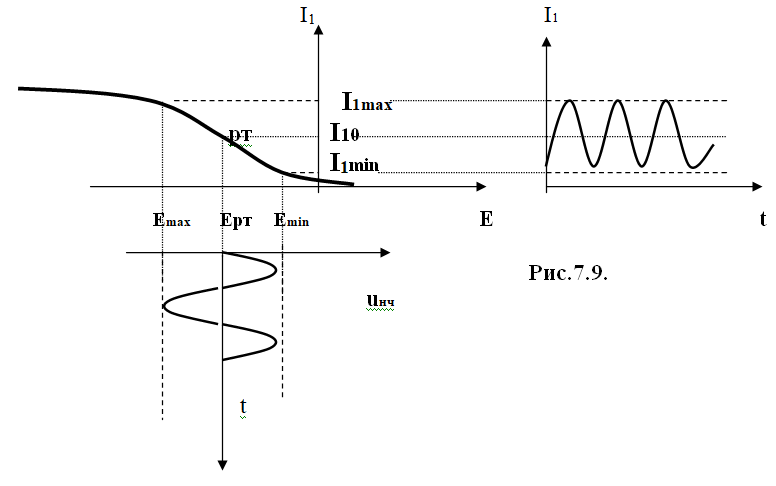
Стандартный вид СМХ показан на рис. 7.9.
Рассмотрим выбор рабочего режима по СМХ.
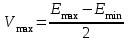
ции для неискажённых АМ:
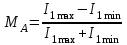
2.ЧМ. Параметры и диаграммы.
Частотная модуляция (ЧМ) — вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.
При ЧМ частота ВЧ колебания (несущей) изменяется в соответствии с НЧ модулирующим сигналом.
чм (t) = 0 + Uнч(t), где
чм (t)- частота ЧМ сигнала;
0- среднее значение несущей частоты;
Uнч(t)-модулирующий сигнал;
-девиация частоты, т.е. максимальное отклонение частоты от среднего значения.
Если модулирующий сигнал гармонический, т.е.
Uнч = cost,
то чм(t) = 0 + соst
а выражение для ЧМ сигнала имеет вид:
чм(t) =
Uчм(t) = Umcos(0t+
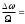Mч - индекс ЧМ. (9.2)
Uчм(t) = Umcos(0t+
Временная диаграмма модулирующего сигнала имеет вид:
Uнч(t)
Рис.9.1.
t
Временная диаграмма соответствующего ЧМ сигнала принимает вид:
Uчм(t)
t
рис 9.2
Как видно из рис.9.2, там, где модулирующий сигнал больше, там и частота ЧМ сигнала больше , а период колебаний меньше.
чм(t) = 0 + cost
max = 0 +
min = 0 -
Амплитуда при ЧМ постоянна, меняется только частота.
Для получения спектра ЧМ сигнала разложим Uчм(t) в ряд Фурье.
Uчм(t) = Umcos(0t+ = Um0(Mч)cos0t+ Um1(Mч)cos(0+)t- Um1(Mч)cos(0)t+Um2(Mч)cos(0+2)t+Um2(Mч)cos(02)t+Um
3(Mч)*cos(0+3)t- Um3(Mч)cos(0-3)t+
k(Mч) - функция Бесселя к-ого порядка.
Вид спектра зависит от Мч.
Спектр ЧМ сигнала при Мч<<1 (т.е. порядка 0,1; 0,05;)
u Um несущая
нижняя MчUm MчUm верхняя
боковая 2 2 боковая
0- 0 0+
Рис.9.3.
При Мч<<1 спектр ЧМ сигнала похож на спектр АМ сигнала (несущая, 2 боковых ), но для ЧМ этот спектр приближенный. Все остальные боковые тоже есть, но они очень малы.
Спектр ЧМ сигнала при Мч>1 выглядит так (Мч=5):
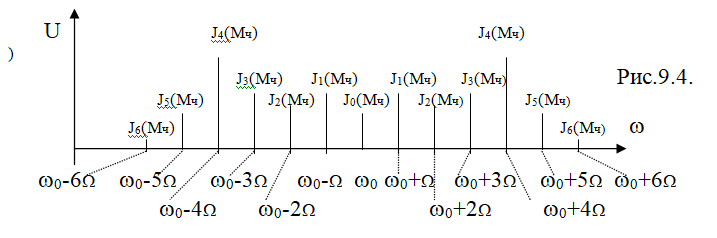
Полоса частот сигнала ЧМ.
Пчм 2(Мч+1)
Мч<<1 Пчм 2, ( как при АМ )
Мч>>1 Пчм 2Мч = 2
2
Ширина спектра при Мч>>1 не зависит от модулирующей частоты. Это широкополосный сигнал.
Билет 20.
1.Амплитудный модулятор. Расчет СМХ (метод угла отсечки) (Амплитудный модулятор в 38)
СМХ – это зависимость амплитуды 1-ой гармоники выходного тока I1 модулятора от напряжения смещения E при амплитуде вч несущей Um=const и амплитуде нч модулирующего сигнала Vm = 0.
Расчет СМХ методом угла отсечки.
1.Аппроксимируем ВАХ отрезками прямых.
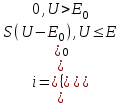S<0; 2. Определяем пределы изменения смещения E.
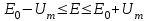
Um – амплитуда несущей.
3. Задаёмся напряжением смещения Е/.
4. Определяем угол отсечки:
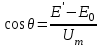
5. Определяем амплитуду первой гармоники:
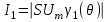, где 1()-коэффициент Берга (см. учебник[1])6.
Возвращаемся в пункт 3 и т.д.Стандартный вид СМХ показан на рис. 7.9.
Рассмотрим выбор рабочего режима по СМХ.
-
Определяем Еmin , Emax , Imax , Imin . -
Выбираем рабочую точку в середине линейного участка Р.Т.(I10;ЕР. Т.) -
Определяем максимальную амплитуду модулирующего сигнала для неискажённой модуляции:
-
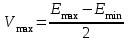
Определяем максимальную глубину амплитудной модуля-
ции для неискажённых АМ:
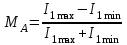
2.ЧМ. Параметры и диаграммы.
Частотная модуляция (ЧМ) — вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.
При ЧМ частота ВЧ колебания (несущей) изменяется в соответствии с НЧ модулирующим сигналом.
чм (t) = 0 + Uнч(t), где
чм (t)- частота ЧМ сигнала;
0- среднее значение несущей частоты;
Uнч(t)-модулирующий сигнал;
-девиация частоты, т.е. максимальное отклонение частоты от среднего значения.
Если модулирующий сигнал гармонический, т.е.
Uнч = cost,
то чм(t) = 0 + соst
а выражение для ЧМ сигнала имеет вид:
чм(t) =
Uчм(t) = Umcos(0t+
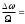Mч - индекс ЧМ. (9.2)Uчм(t) = Umcos(0t+
Временная диаграмма модулирующего сигнала имеет вид:
Uнч(t) Рис.9.1. tВременная диаграмма соответствующего ЧМ сигнала принимает вид:
Uчм(t)
t
рис 9.2
Как видно из рис.9.2, там, где модулирующий сигнал больше, там и частота ЧМ сигнала больше , а период колебаний меньше.
чм(t) = 0 + cost
max = 0 +
min = 0 -
Амплитуда при ЧМ постоянна, меняется только частота.
Для получения спектра ЧМ сигнала разложим Uчм(t) в ряд Фурье.
Uчм(t) = Umcos(0t+
= Um0(Mч)cos0t+ Um1(Mч)cos(0+)t- Um1(Mч)cos(0)t+Um2(Mч)cos(0+2)t+Um2(Mч)cos(02)t+Um
3(Mч)*cos(0+3)t- Um3(Mч)cos(0-3)t+
k(Mч) - функция Бесселя к-ого порядка.
Вид спектра зависит от Мч.
Спектр ЧМ сигнала при Мч<<1 (т.е. порядка 0,1; 0,05;)
u Um несущая нижняя MчUm MчUm верхняя
боковая 2 2 боковая 0- 0 0+
Рис.9.3.
При Мч<<1 спектр ЧМ сигнала похож на спектр АМ сигнала (несущая, 2 боковых ), но для ЧМ этот спектр приближенный. Все остальные боковые тоже есть, но они очень малы.
Спектр ЧМ сигнала при Мч>1 выглядит так (Мч=5):
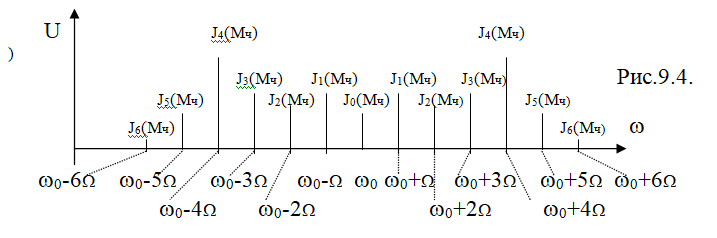
Полоса частот сигнала ЧМ.
Пчм 2(Мч+1)
Мч<<1 Пчм 2, ( как при АМ )
Мч>>1 Пчм 2Мч = 2
2Ширина спектра при Мч>>1 не зависит от модулирующей частоты. Это широкополосный сигнал.