Задания по теме “Случайные величины”Вариант 11. Стрелок делает по мишени 3 выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Составить ряд и функцию распределения случайной величины – общего числа попаданий.2. Дискретная случайная величина может принимать только два значения и , причем . Известны вероятность появления значения , математическое ожидание . Составить закон распределения этой случайной величины и найти дисперсию .3. Случайная величина имеет плотность распределения.Найти: параметр A, математическое ожидание M(X), дисперсию D(X), функцию распределения F(x).4. Всхожесть семян данного сорта растений оценивается с вероятностью 0,6. Найти математическое ожидание и дисперсию случайной величиныХ – числа семян, которые взойдут из 40 посеянных семян.5. Случайная величина X подчинена нормальному закону с математическим ожиданием a и средним квадратическим отклонением . Вычислить с точностью до 0,01 вероятность попадания X в интервал (a, a+ ).Вариант 21. В урне 5 белых и 5 черных шаров. Вынули два шара. Случайная величина X – число вынутых белых шаров. Составить ряд и функцию распределения этой случайной величины.2. Дискретная случайная величина

---

может принимать только два значения и , причем . Известны вероятность появления возможного значения , математическое ожидание . Составить закон распределения этой случайной величины и найти дисперсию .

3. Случайная величина задана плотностью распределения вероятности

.

Найти: параметр A, математическое ожидание M(X), дисперсию D(X), функцию распределения F(x).

4. Вероятность промаха в цель равна 0,3. Случайная величина X – число попаданий при 10 выстрелах. Найти математическое ожидание и дисперсию этой случайной величины.

5. Определить среднее квадратическое отклонение ошибки прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и не выходят за пределы ±20 м с вероятностью 0,6.

Вариант 3

1. Вероятность всхода семян некоторого растения равна 0,8. Посеяно три семени. Составить закон и функцию распределения случайной величины Х – числа взошедших семян.

2. Дискретная случайная величина может принимать только два значения и , причем . Известны вероятность появления возможного значения , математическое ожидание . Составить закон распределения этой случайной величины и найти дисперсию

---

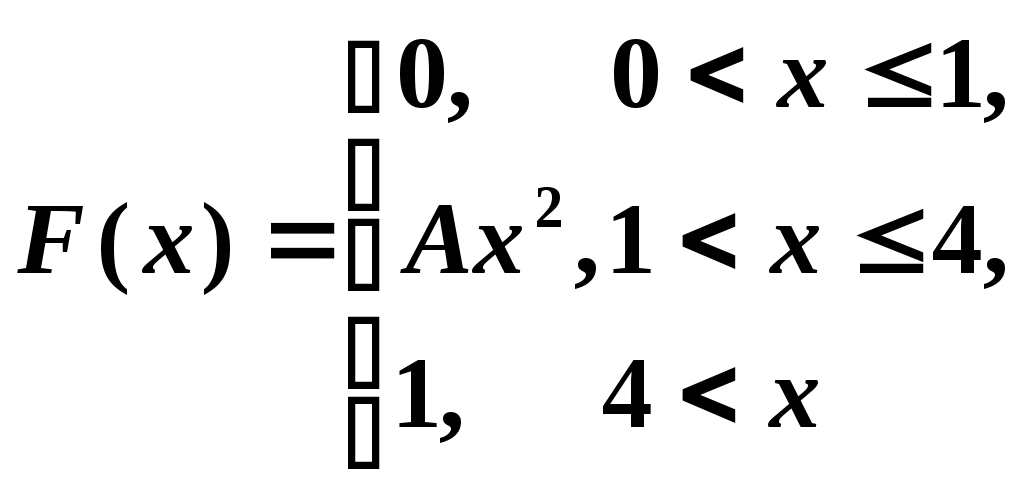
.3. Случайная величина задана интегральной функцией распределенияНайти: параметр A, математическое ожидание M(X), дисперсию D(X), плотность распределения f(x).4. Устройство состоит из 20 независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте 0,3. Найти математическое ожидание и дисперсию случайной величиныХ – числа отказавших элементов в одном опыте.5. Среднее квадратическое отклонение ошибки измерения дальности радиолокатора равно 20 метрам. Систематической ошибки нет. Найти вероятность получения ошибки измерения дальности, по абсолютной величине не превосходящей 15 метров.Вариант 41. Производится испытание трех изделий на надежность. Вероятность выдержать испытание для каждого изделия равна 0,7. Составить ряд и функцию распределения случайной величины Х – числа изделий, выдержавших испытания.2. Дискретная случайная величина может принимать только два значения и , причем . Известны вероятность появления возможного значения , математическое ожидание . Составить закон распределения этой случайной величины и найти дисперсию .3. 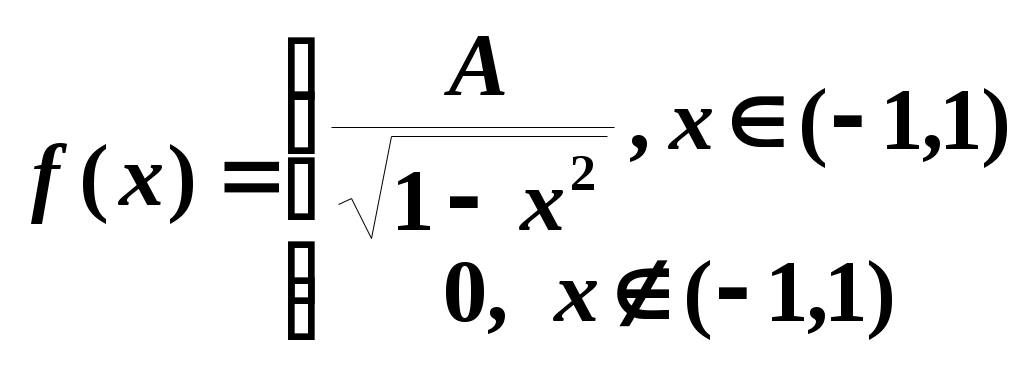Плотность распределения вероятностей случайной величины задана функциейНайти: параметр A, математическое ожидание M(X), вероятность P(1/2 функцию распределения F(x).4. Коммутатор учреждения обслуживает 60 абонентов. Вероятность того, что в течение одной минуты абонент позвонит, равна

---

0,1. Случайная величина X – число абонентов, позвонивших в течение минуты. Найти математическое ожидание и дисперсию этой случайной величины.5. Случайная ошибка измерительного прибора подчинена нормальному закону распределения с дисперсией 25 . Систематическая ошибка отсутствует. Определить вероятность того, что ошибка измерения по модулю не превзойдет величины 6 мк.Вариант 51. Три стрелка независимо друг от друга стреляют по мишени. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,9, для третьего – 0,7. Построить ряд и функцию распределения случайной величины Х – общего числа попаданий.2. Дискретная случайная величина может принимать только два значения и , причем . Известны вероятность появления возможного значения , математическое ожидание . Составить закон распределения этой случайной величины и найти дисперсию .3. Случайная величина задана интегральной функцией распределения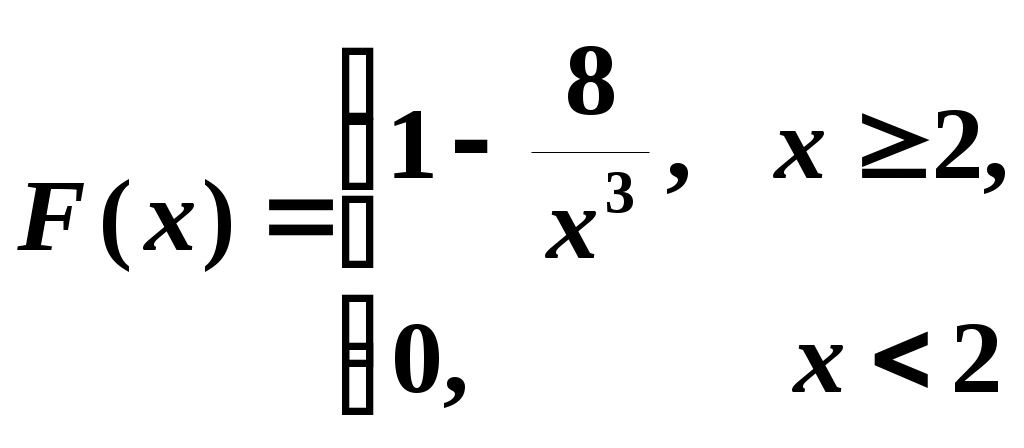.Найти: математическое ожидание M(X), вероятность p(1 плотность распределения f(x).4. Батарея дала 16 выстрелов по объекту. Вероятность попадания в каждом выстреле 0,7. Найти математическое ожидание M(X) числа попаданий и дисперсию.5. Случайная величина X подчинена нормальному закону с математическим ожиданием a и средним квадратическим отклонением . Вычислить с точностью до 0,01 вероятности попадания X в интервал (a+2, a+3).Вариант 61. В мастерской работает три мотора. Вероятность того, что мотор в данный момент работает с полной нагрузкой, равна

---

0,9. Составить ряд и функцию распределения случайной величины X – общего числа работающих с полной нагрузкой моторов.2. Дискретная случайная величина может принимать только два значения и , причем . Известны вероятность появления возможного значения , математическое ожидание . Составить закон распределения этой случайной величины и найти дисперсию .3. Дифференциальный закон распределения случайной величины X имеет вид: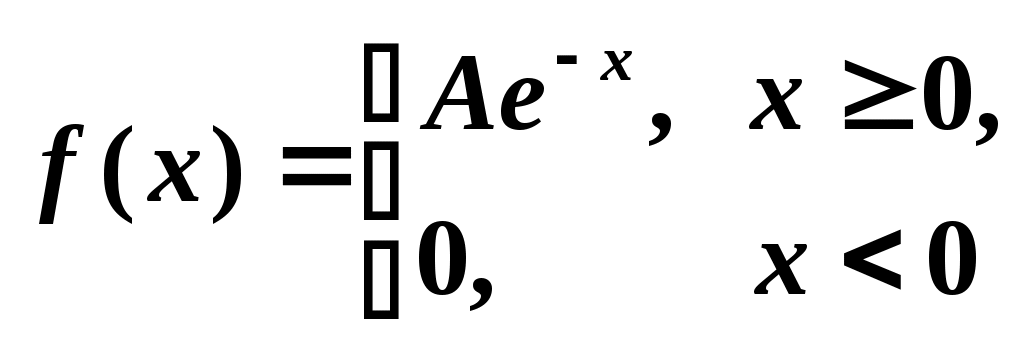.Найти коэффициент A, математическое ожидание M(X), вероятность P(1 функцию распределения F(x).4. Вероятность попадания в цель при каждом выстреле равна 0,2. Найти математическое ожидание случайной величиныХ – числа попаданий при 40 выстрелах.5. Производится взвешивание крупы без систематических погрешностей. Случайные погрешности подчинены нормальному закону со стандартным отклонением 15 г. Найти вероятность того, что взвешивание произведено с погрешностью не превосходящей по модулю 6 г.Вариант 71. Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,4, для второго – 0,9, для третьего – 0,8. Построить закон и функцию распределения случайной величины Х – общего числа станков, не потребовавших внимания рабочего.2. Дискретная случайная величина может принимать только два значения

---

Смотрите также файлы

• 1. Роль экономической теории в развитии хозяйства и ее место в системе экономических наук.docx

• Технологии разработки программного обеспечения.ppt

• Ответ диклофенакнатрий.docx

• Практическое задание Дайте характеристику методам специальной психологии (методам профилактики, методам воздействия и т д.). Методы специальной психологии делят на 3 большие группы Метод.docx

• Сущность экономического роста национальной экономики Характеристики экономического роста.docx