ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 183
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
и  , причем
, причем  . Известны вероятность появления
. Известны вероятность появления 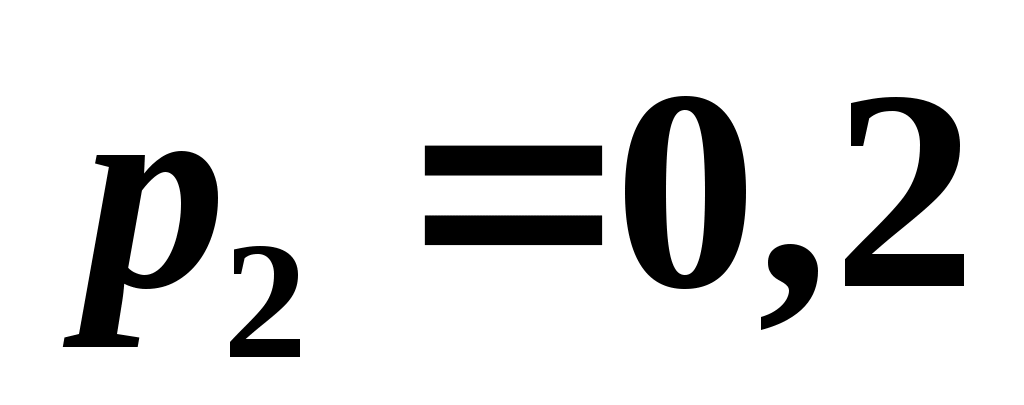 возможного значения
возможного значения 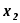 , математическое ожидание
, математическое ожидание 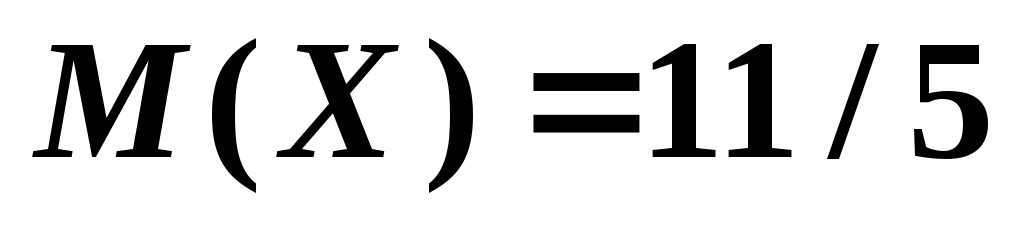 . Составить закон распределения этой случайной величины и найти дисперсию
. Составить закон распределения этой случайной величины и найти дисперсию  .
.
3. Интегральная функция распределения имеет вид:
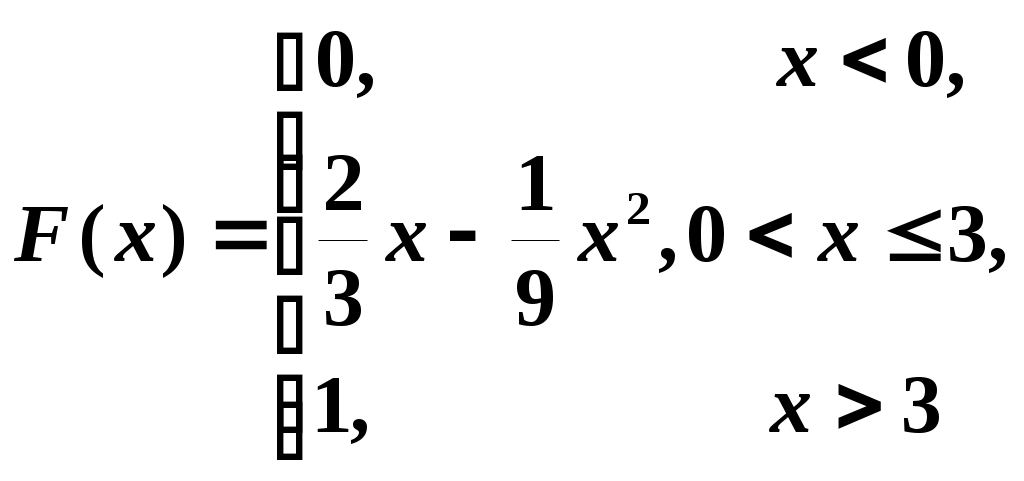 .
.
Найти: математическое ожидание M(X), дисперсию D(X), плотность распределения f(x).
4. В лаборатории работают 16 независимых приборов. Вероятность того, что в данный момент прибор работает – 0,9. Найти математическое ожидание и дисперсию числа работающих в данный момент приборов.
5. Случайная величина – ошибка измерений – распределена по нормальному закону. Найти вероятность того, что она примет значение между (-2, 3), если систематические погрешности отсутствуют. Здесь – стандартное отклонение.
Вариант 8
1. В некотором цехе брак составляет в среднем 10 % всех изделий. Наугад взяты 3 изделия. Построить ряд и функцию распределения случайной величины Х – числа бракованных изделий в выборке. (Считать число выпускаемых изделий достаточно большим).
2. Дискретная случайная величина может принимать только два значения
может принимать только два значения  и
и 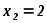 , причем
, причем  . Известны вероятность появления
. Известны вероятность появления 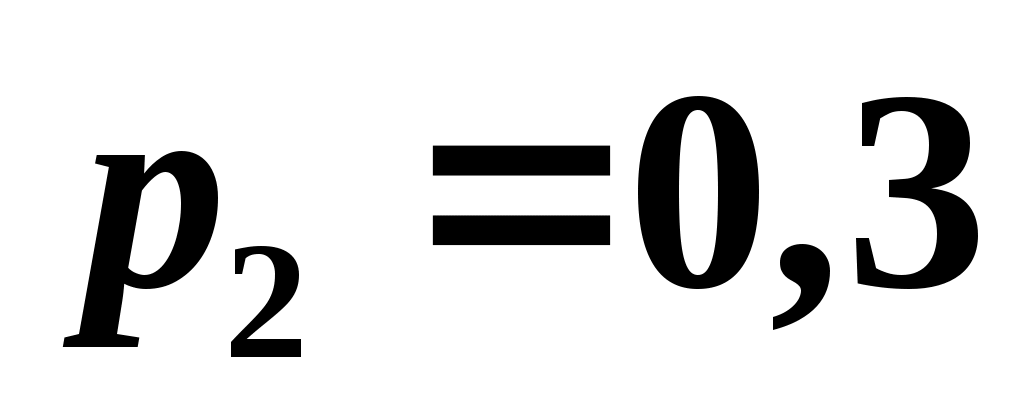 возможного значения
возможного значения 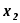 , математическое ожидание
, математическое ожидание 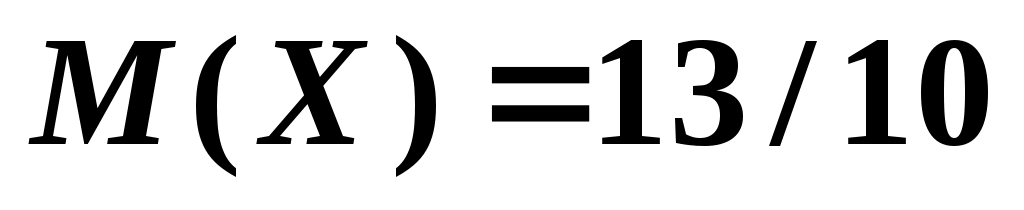
. Составить ряд распределения случайной величины и найти дисперсию
и найти дисперсию  .
.
3. Плотность распределения вероятностей случайной величины задана функцией
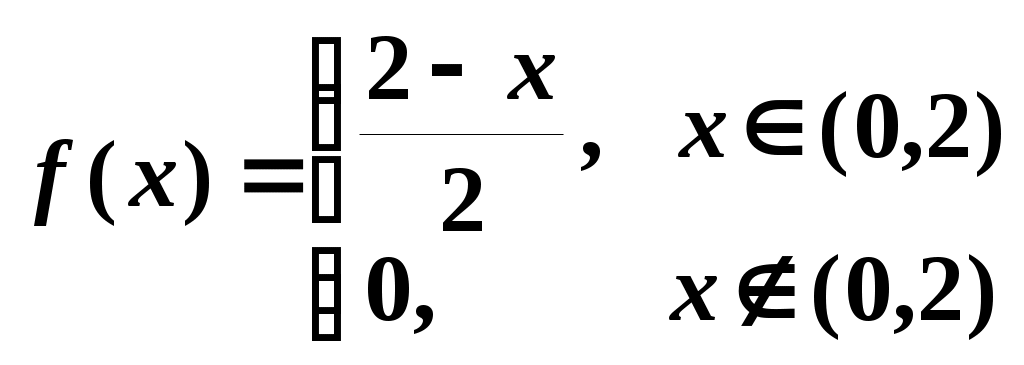 .
.
Найти: математическое ожидание M(X), дисперсию D(X), функцию распределения F(x), вероятность P(-1
4. Найти математическое ожидание и дисперсию случайной величины X – числа лотерейных билетов и, на которые выпадут выигрыши, если приобретено 30 билетов, причем, вероятность выигрыша по одному билету равна 0,04.
5. Измерение диаметра вала производится без систематических ошибок. Случайные ошибки распределены по нормальному закону со средним квадратическим отклонением 8 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по модулю 9 мм.
Вариант 9
1. Из десяти ламп три дефектные. Для проверки отобраны случайным образом три лампы. Построить ряд и функцию распределения случайной величины Х – числа дефектных ламп в выборке.
2. Дискретная случайная величина может принимать только два значения
может принимать только два значения  и
и  , причем
, причем  . Известны вероятность появления
. Известны вероятность появления 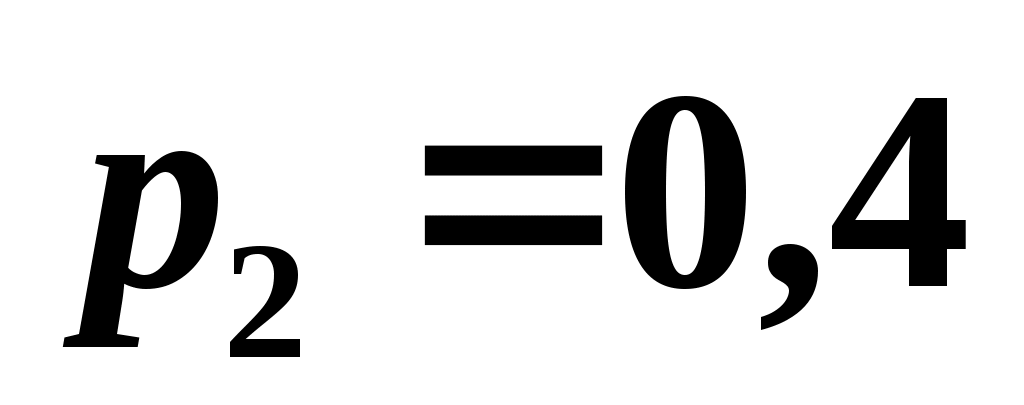 возможного значения
возможного значения  , математическое ожидание
, математическое ожидание  . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  и найти дисперсию
и найти дисперсию  .
.
3. Плотность распределения вероятностей случайной величины задана функцией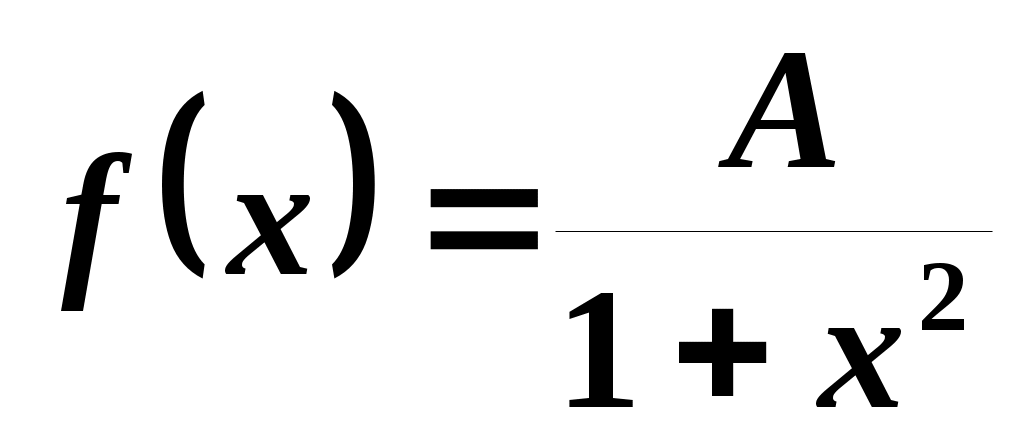 на всей оси. Найти: параметр
на всей оси. Найти: параметр
A, математическое ожидание M(X), функцию распределения F(x).
4. Проводятся 25 независимых испытаний, в каждом из которых вероятность успеха равна 0,1. НайтиD(X) случайной величины X – числа успехов в этих испытаниях.
5. Автомат штампует шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,6 мм. Считая, что величина Х распределена по нормальному закону со стандартным отклонением = 0,3, найти среднее число годных шариков из ста изготовленных.
Вариант 10
1. Построить ряд и функцию распределения случайной величины Х – общего числа попаданий мячом в корзину при трех бросках, если вероятность попадания при одном броске равна 0,7.
2. Дискретная случайная величина может принимать только два значения
может принимать только два значения  и
и  , причем
, причем  . Известны вероятность появления
. Известны вероятность появления 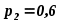 возможного значения
возможного значения  , математическое ожидание
, математическое ожидание 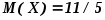 . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  и найти дисперсию
и найти дисперсию  .
.
3. Дана функция плотности распределения случайной величины X:
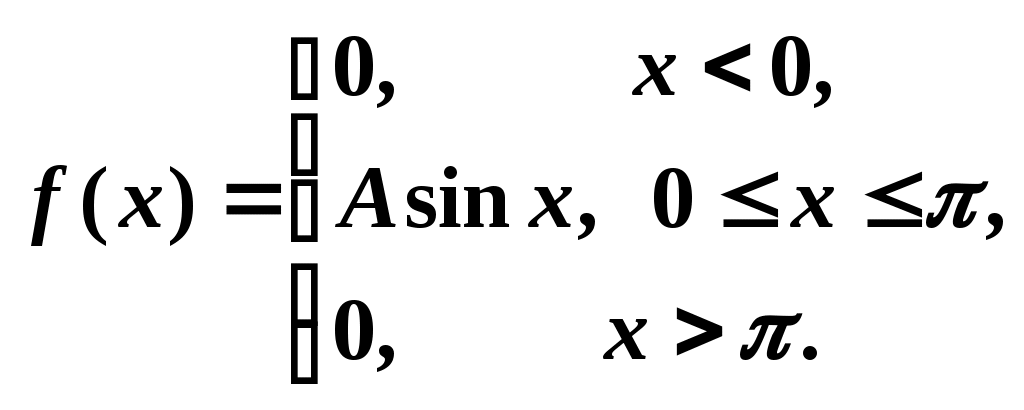 .
.
Найти коэффициент A, математическое ожидание M(X), функцию распределения F(x), вероятность p(-
4. Устройство состоит из 30 независимо работающих элементов. Вероятность отказа элемента за определенное время равна 0,3. Дискретная случайная величина
X – число отказавших элементов за данное время. Найти дисперсию D(X).
5. Деталь, изготовленная на станке, считается годной, если отклонение ее контролируемого размера от проектного не превышает 8 мм. Случайные отклонения распределены по нормальному закону с математическим ожиданием равным нулю и средним квадратическим отклонением равным 4 мм. Какой процент годных деталей изготовляется на станке?
Вариант 11
1. Вероятность покупки сумки равна 0,3, туфель – 0,2, а портфеля – 0,4. Составить закон и функцию распределения случайной величины Х – общего числа совершенных покупок.
2. Случайная величина X задана таблицей распределения:
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Плотность распределения вероятностей случайной величины задана функцией:
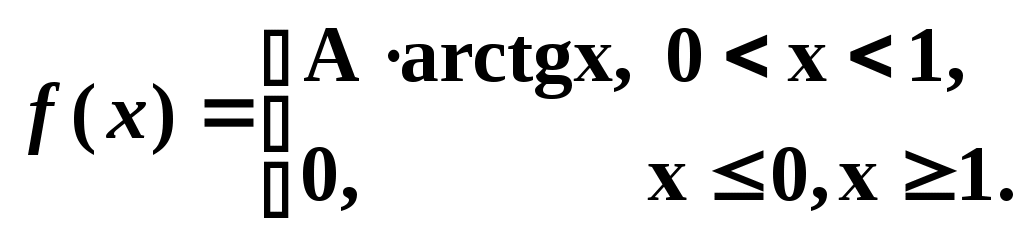
Найти: параметр A, математическое ожидание M(X), вероятность P(0
4. Вероятность появления события при одном испытании равна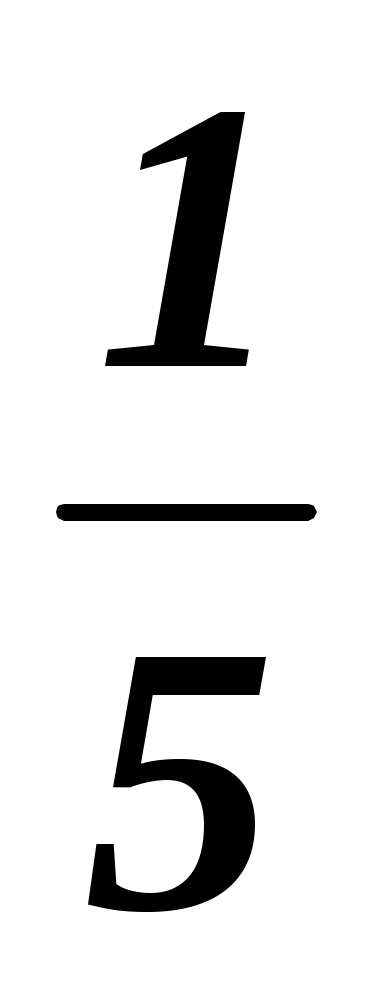 . Найти математическое ожидание M(X) случайной величины X – числа появления события при 20 независимых испытаниях.
. Найти математическое ожидание M(X) случайной величины X – числа появления события при 20 независимых испытаниях.
5. Ошибки измерения скорости подчинены нормальному закону распределения со средним квадратическим отклонением 15 км/час. И центром рассеивания a = 0. Найти вероятность того, что ошибка измерения скорости будет не более 30 км/час по абсолютной величине.
Вариант 12
1. В киоске осталось по одному экземпляру газет “Алтайская правда”, “Вечерний Барнаул”, “Известия”. Вероятность реализации в течение часа первой газеты равна 0,6, второй – 0,3, третьей – 0,4. Составить ряд и функцию распределения случайной величины X – числа проданных в течение часа газет.
2. Случайная величина X задана таблицей распределения:
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Случайная величина Xзадана интегральной функцией распределения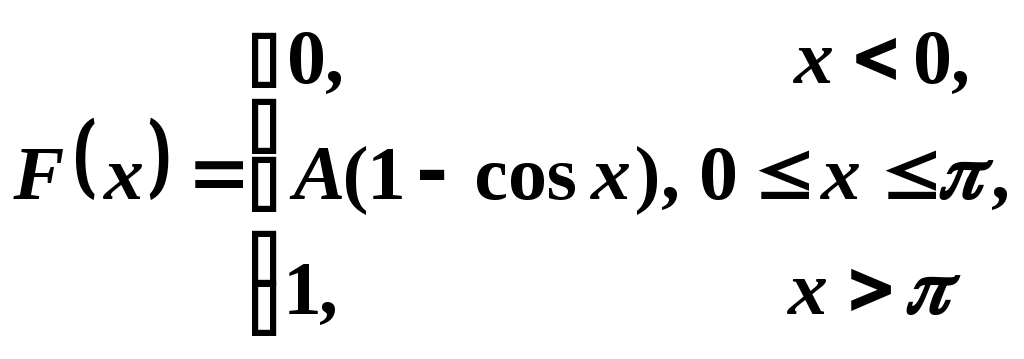 .
.
Найти: параметр A, математическое ожидание M(X), дисперсию D(X), плотность распределения f(x).
4. Случайная величина X – число появлений события A в 30 независимых испытаниях. Вероятность появления A в одном испытании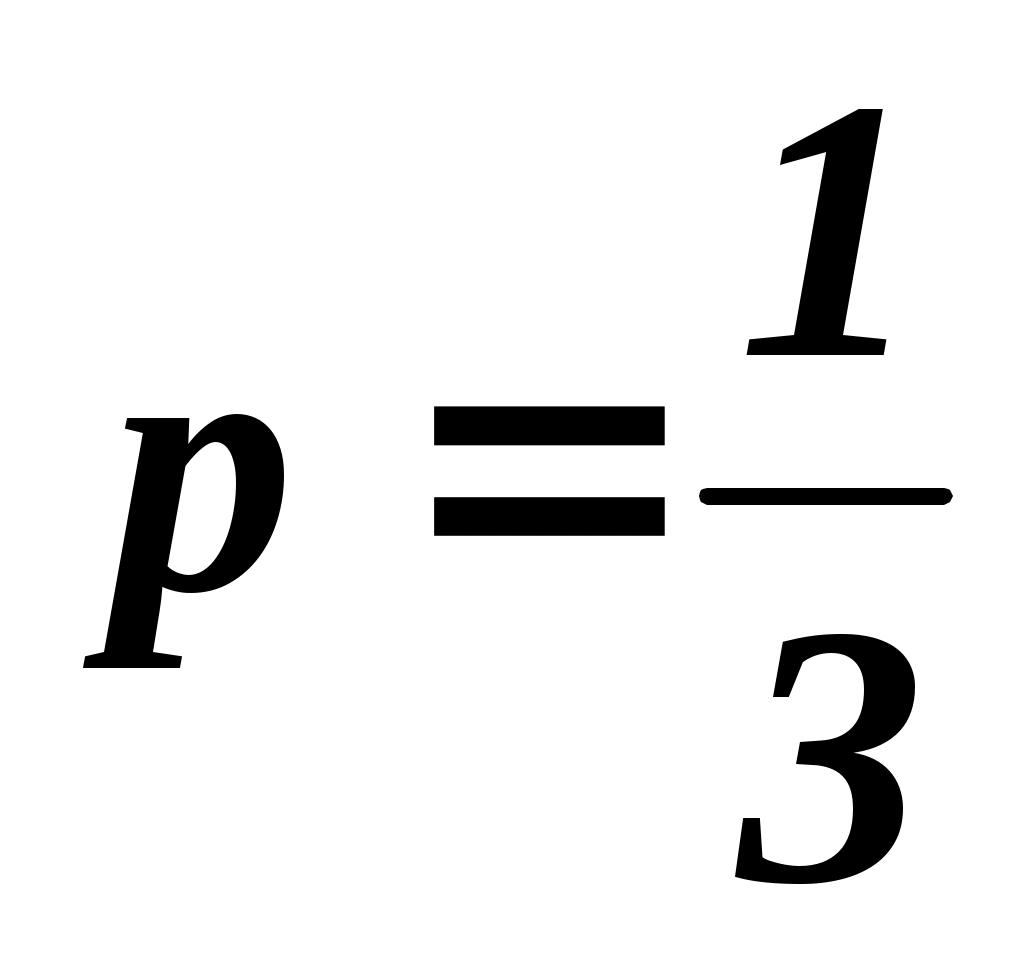 . Найти математическое ожидание M(X) и дисперсию D(X).
. Найти математическое ожидание M(X) и дисперсию D(X).
5. Измерительный прибор имеет среднюю квадратическую ошибку 45 м и не имеет систематической ошибки. Найти вероятность того, что ошибка измерения не превзойдет по абсолютной величине 6 м.
Вариант 13
1. Вероятность успешной сдачи экзамена по математике для первого студента равна 0,8, для второго – 0,7, для третьего – 0,3. Построить ряд и функцию распределения случайной величины X – числа студентов, успешно сдавших экзамен по математике.
2. Случайная величина X задана таблицей распределения:
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Случайная величина задана интегральной функцией распределения: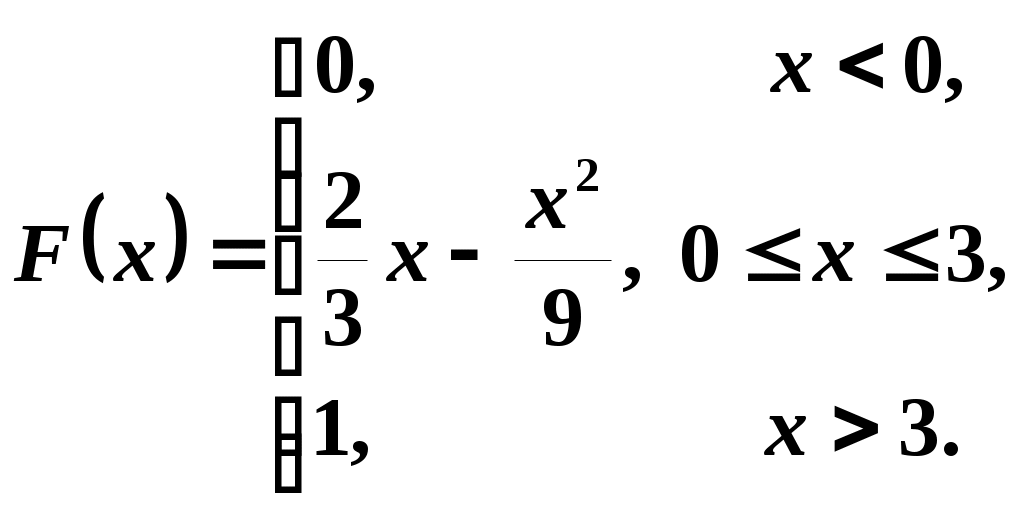
Требуется найти: функцию плотности распределения вероятности и среднее квадратичное отклонение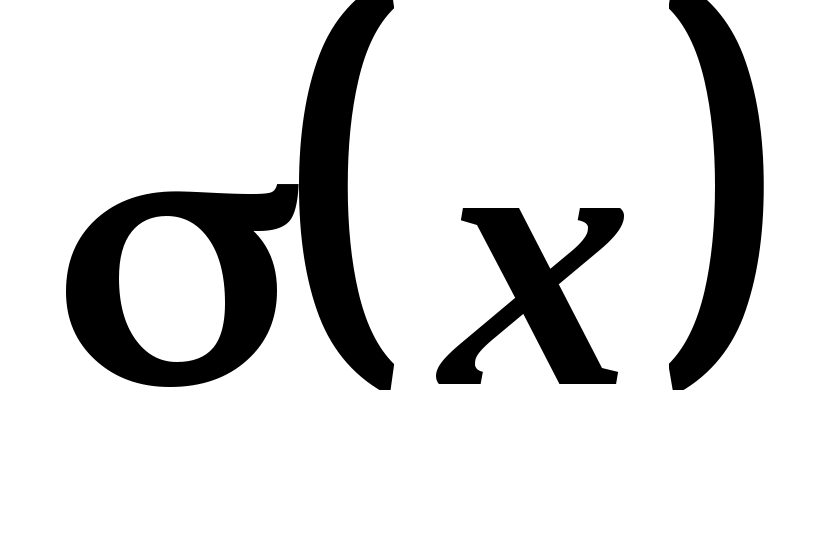 .
.
4. Всхожесть семян данного сорта растений оценивается с вероятностью 0,7. Найти математическое ожидание и дисперсию случайной величиныХ – числа семян, которые взойдут из 30 посеянных семян.
5. Высотомер измеряет высоту с ошибкой, починенной нормальному закону со стандартным отклонением 50 м. Систематической ошибки нет. Найти вероятность того, что ошибка измерения не выйдет из пределов 60 м.
Вариант 14
1. Установлено, что в среднем
3. Интегральная функция распределения имеет вид:
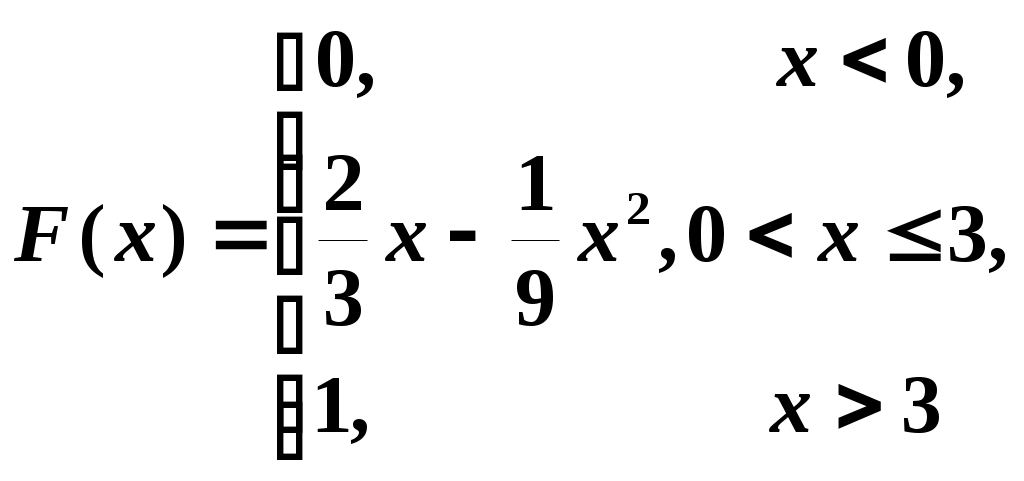 .
.Найти: математическое ожидание M(X), дисперсию D(X), плотность распределения f(x).
4. В лаборатории работают 16 независимых приборов. Вероятность того, что в данный момент прибор работает – 0,9. Найти математическое ожидание и дисперсию числа работающих в данный момент приборов.
5. Случайная величина – ошибка измерений – распределена по нормальному закону. Найти вероятность того, что она примет значение между (-2, 3), если систематические погрешности отсутствуют. Здесь – стандартное отклонение.
Вариант 8
1. В некотором цехе брак составляет в среднем 10 % всех изделий. Наугад взяты 3 изделия. Построить ряд и функцию распределения случайной величины Х – числа бракованных изделий в выборке. (Считать число выпускаемых изделий достаточно большим).
2. Дискретная случайная величина
. Составить ряд распределения случайной величины
3. Плотность распределения вероятностей случайной величины задана функцией
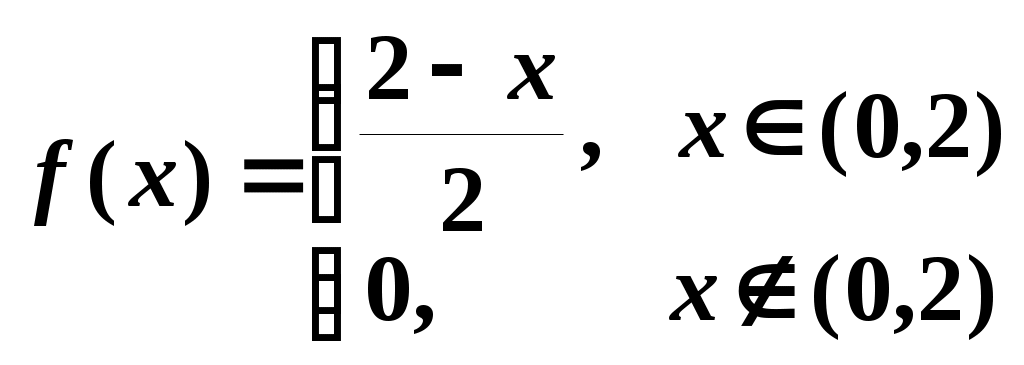 .
.Найти: математическое ожидание M(X), дисперсию D(X), функцию распределения F(x), вероятность P(-1
4. Найти математическое ожидание и дисперсию случайной величины X – числа лотерейных билетов и, на которые выпадут выигрыши, если приобретено 30 билетов, причем, вероятность выигрыша по одному билету равна 0,04.
5. Измерение диаметра вала производится без систематических ошибок. Случайные ошибки распределены по нормальному закону со средним квадратическим отклонением 8 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по модулю 9 мм.
Вариант 9
1. Из десяти ламп три дефектные. Для проверки отобраны случайным образом три лампы. Построить ряд и функцию распределения случайной величины Х – числа дефектных ламп в выборке.
2. Дискретная случайная величина
3. Плотность распределения вероятностей случайной величины задана функцией
A, математическое ожидание M(X), функцию распределения F(x).
4. Проводятся 25 независимых испытаний, в каждом из которых вероятность успеха равна 0,1. НайтиD(X) случайной величины X – числа успехов в этих испытаниях.
5. Автомат штампует шарики. Шарик считается годным, если отклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,6 мм. Считая, что величина Х распределена по нормальному закону со стандартным отклонением = 0,3, найти среднее число годных шариков из ста изготовленных.
Вариант 10
1. Построить ряд и функцию распределения случайной величины Х – общего числа попаданий мячом в корзину при трех бросках, если вероятность попадания при одном броске равна 0,7.
2. Дискретная случайная величина
3. Дана функция плотности распределения случайной величины X:
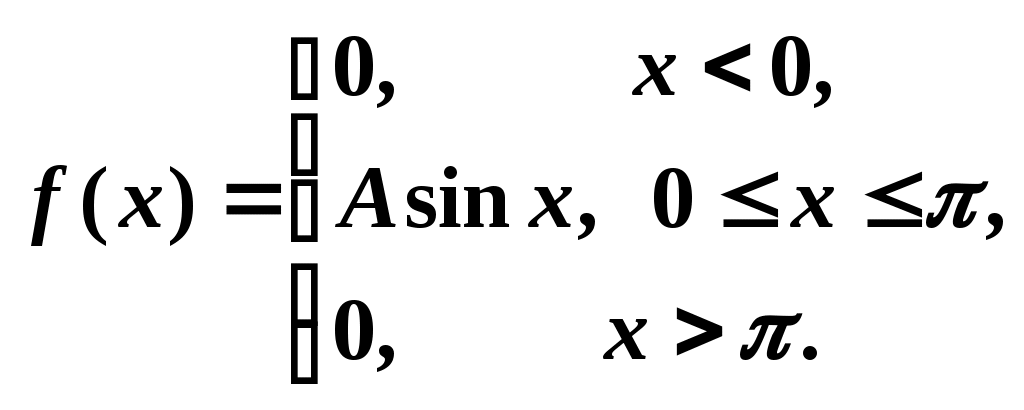 .
.Найти коэффициент A, математическое ожидание M(X), функцию распределения F(x), вероятность p(-
4. Устройство состоит из 30 независимо работающих элементов. Вероятность отказа элемента за определенное время равна 0,3. Дискретная случайная величина
X – число отказавших элементов за данное время. Найти дисперсию D(X).
5. Деталь, изготовленная на станке, считается годной, если отклонение ее контролируемого размера от проектного не превышает 8 мм. Случайные отклонения распределены по нормальному закону с математическим ожиданием равным нулю и средним квадратическим отклонением равным 4 мм. Какой процент годных деталей изготовляется на станке?
Вариант 11
1. Вероятность покупки сумки равна 0,3, туфель – 0,2, а портфеля – 0,4. Составить закон и функцию распределения случайной величины Х – общего числа совершенных покупок.
2. Случайная величина X задана таблицей распределения:
| X | -3 | 1 | 2 |
| P | 0,1 | А | 0,2 |
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Плотность распределения вероятностей случайной величины задана функцией:
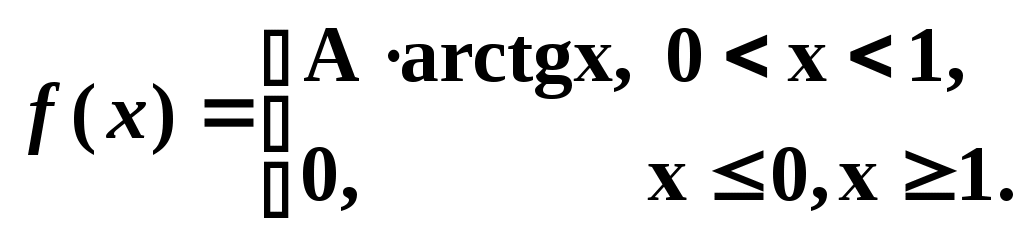
Найти: параметр A, математическое ожидание M(X), вероятность P(0
4. Вероятность появления события при одном испытании равна
5. Ошибки измерения скорости подчинены нормальному закону распределения со средним квадратическим отклонением 15 км/час. И центром рассеивания a = 0. Найти вероятность того, что ошибка измерения скорости будет не более 30 км/час по абсолютной величине.
Вариант 12
1. В киоске осталось по одному экземпляру газет “Алтайская правда”, “Вечерний Барнаул”, “Известия”. Вероятность реализации в течение часа первой газеты равна 0,6, второй – 0,3, третьей – 0,4. Составить ряд и функцию распределения случайной величины X – числа проданных в течение часа газет.
2. Случайная величина X задана таблицей распределения:
| X | -2 | 2 | 5 |
| P | 0,2 | 0,3 | A |
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Случайная величина Xзадана интегральной функцией распределения
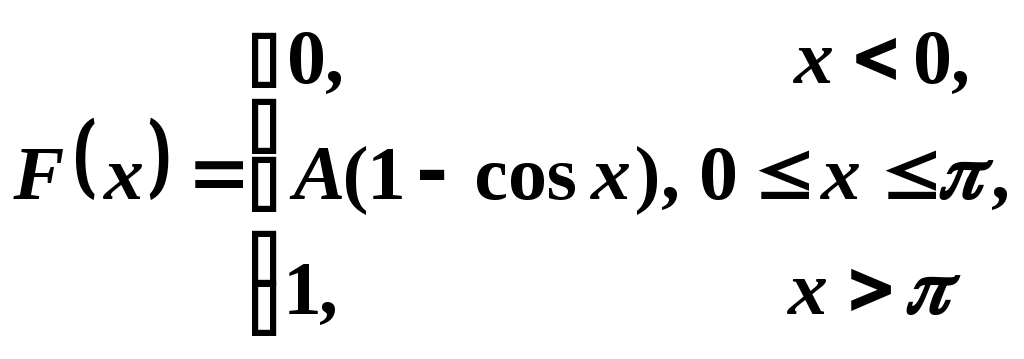 .
.Найти: параметр A, математическое ожидание M(X), дисперсию D(X), плотность распределения f(x).
4. Случайная величина X – число появлений события A в 30 независимых испытаниях. Вероятность появления A в одном испытании
5. Измерительный прибор имеет среднюю квадратическую ошибку 45 м и не имеет систематической ошибки. Найти вероятность того, что ошибка измерения не превзойдет по абсолютной величине 6 м.
Вариант 13
1. Вероятность успешной сдачи экзамена по математике для первого студента равна 0,8, для второго – 0,7, для третьего – 0,3. Построить ряд и функцию распределения случайной величины X – числа студентов, успешно сдавших экзамен по математике.
2. Случайная величина X задана таблицей распределения:
| X | -2 | 0 | 5 |
| P | 0,1 | 0,2 | A |
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Случайная величина задана интегральной функцией распределения:
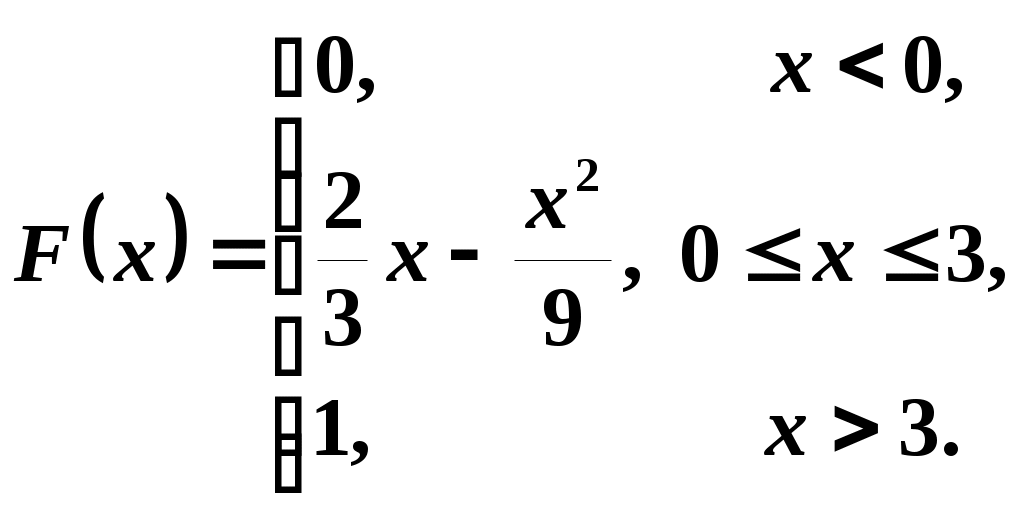
Требуется найти: функцию плотности распределения вероятности и среднее квадратичное отклонение
4. Всхожесть семян данного сорта растений оценивается с вероятностью 0,7. Найти математическое ожидание и дисперсию случайной величиныХ – числа семян, которые взойдут из 30 посеянных семян.
5. Высотомер измеряет высоту с ошибкой, починенной нормальному закону со стандартным отклонением 50 м. Систематической ошибки нет. Найти вероятность того, что ошибка измерения не выйдет из пределов 60 м.
Вариант 14
1. Установлено, что в среднем