ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 181
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
5 % роликов, изготовленных для подшипников, оказываются бракованными. Составить ряд и функцию распределения числа бракованных роликов среди трех проверенных.
2. Случайная величина X задана таблицей распределения:
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Случайная величина X задана дифференциальной функцией распределения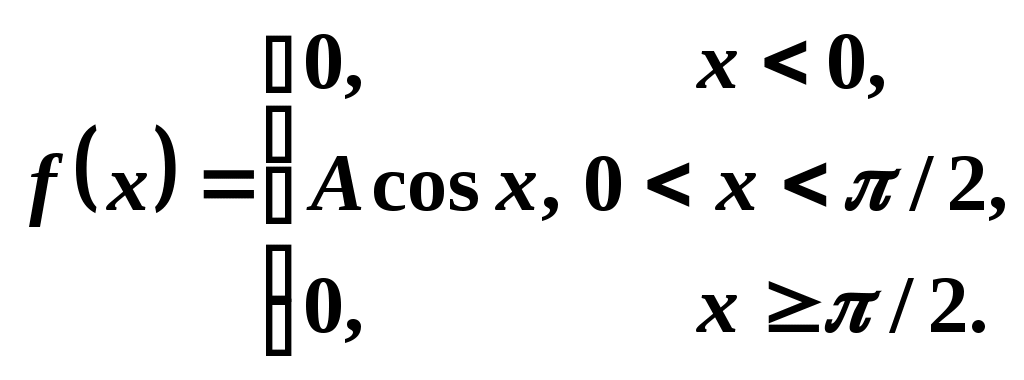
Требуется найти параметр A, математическое ожидание M(X), дисперсию D(X), функцию распределения F(x).
4. Вероятность промаха в цель равна 0,2. Случайная величина X – число попаданий при 40 выстрелах. Найти дисперсию этой случайной величины.
5. Дальномерное устройство измеряет дальность до цели с ошибкой, подчиненной нормальному закону распределения. Среднее квадратическое отклонение ошибки равно 6 м, систематической ошибки нет. Определить вероятность того, что отклонение измеренного значения дальности от истинного не превзойдет значения 5 м.
Вариант 15
1. Вероятность изготовления на автоматическом станке стандартной детали равна 0,7. Написать ряд и функцию распределения случайной величины Х –числа бракованных деталей среди трех наудачу выбранных.
2. Случайная величина X задана таблицей распределения:
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Плотность распределения случайной величины задана функцией:
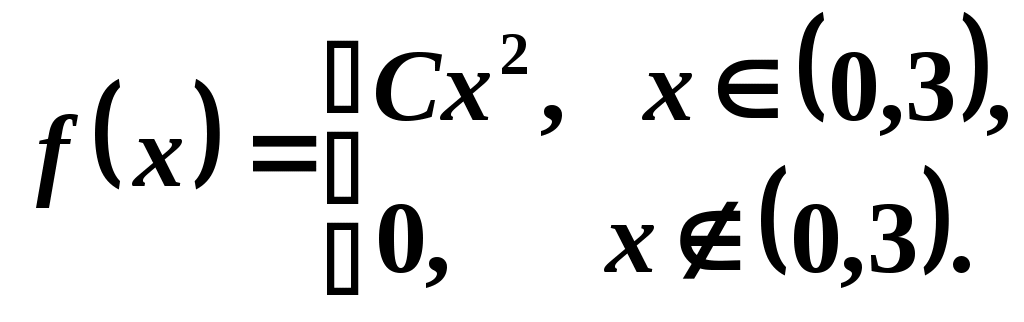 .
.
Найти: параметр C, математическое ожидание M(X), дисперсию D(X), функцию распределения F(x)
.
4. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте 0,2. Найти дисперсию случайной величиныХ – числа отказавших элементов в одном опыте.
5. Контролируемая длина детали распределена по нормальному закону и имеет математическое ожидание 25 см. Вероятность того, что длина изготовленной детали окажется в пределах (10, 18) равна 0,45. Найти вероятность того, что длина изготовленной детали окажется в пределах (32, 40).
Вариант 16
Найти параметр A, математическое ожидание M(X), дисперсию.
3. Случайная величина X задана дифференциальной функцией распределения
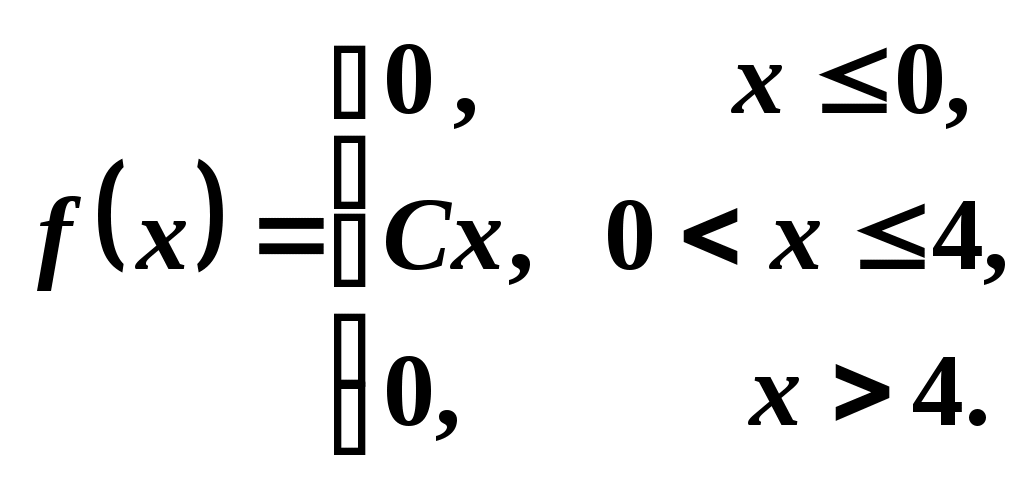 .
.
Требуется: найти параметр C, интегральную функцию распределения, вероятность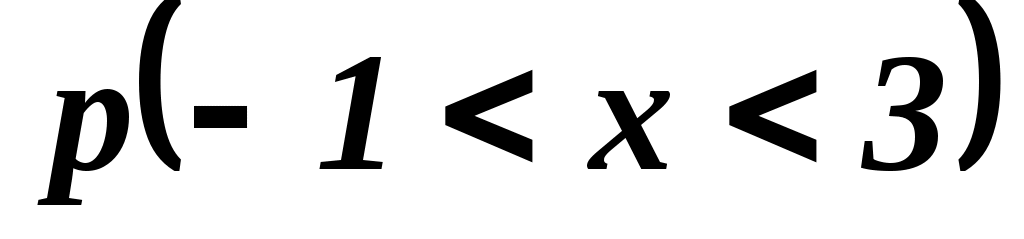 и дисперсию D(X).
и дисперсию D(X).
4. Коммутатор учреждения обслуживает 50 абонентов. Вероятность того, что в течение одной минуты абонент позвонит, равна 0,15. Случайная величина X – число абонентов, позвонивших в течение минуты. Найти математическое ожидание и дисперсию.
5. Вертолет производит одиночное бомбометание по автостраде шириной 16 м, заходя на цель вдоль автострады и прицеливаясь по ее центральной линии. Среднее квадратическое отклонение в боковом направлении равно 20 м. Найти вероятность попадания в цель, если отсутствует систематическая ошибка, а случайная ошибка распределена по нормальному закону.
Вариант 17
1. Монету бросают 3 раза. Найти ряд и функцию распределения случайной величины X – числа выпадений решетки.
2. Случайная величина X задана таблицей распределения:
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Случайная величина X задана дифференциальной функцией распределения:
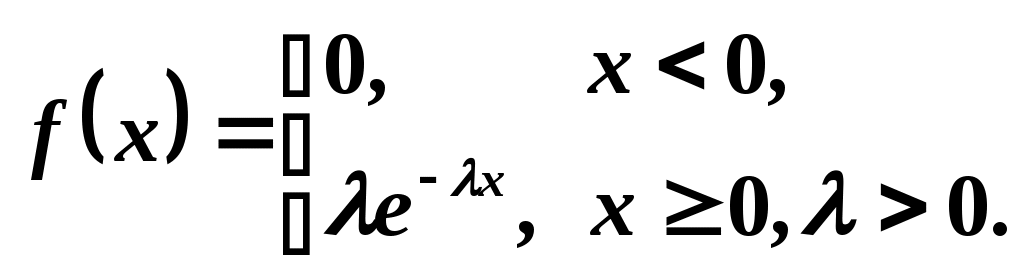 .
.
Найти F(x), математическое ожидание M(X). Найти вероятность того, что X примет значение большее, чем её математическое ожидание.
4. Батарея дала 20 выстрелов по объекту. Вероятность попадания в каждом выстреле 0,6. Найти математическое ожидание и дисперсию числа попаданий.
5. Измерительный прибор имеет среднюю квадратическую ошибку 24 м и не имеет систематической ошибки. Найти вероятность того, что ошибка измерения окажется в пределах 8 м.
Вариант 18
1. Игральную кость бросают 3 раза. Написать ряд распределения и функцию распределения случайной величины X — числа выпадения пятерки.
2. Случайная величина X задана таблицей распределения:
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Случайная величина задана интегральной функцией распределения:
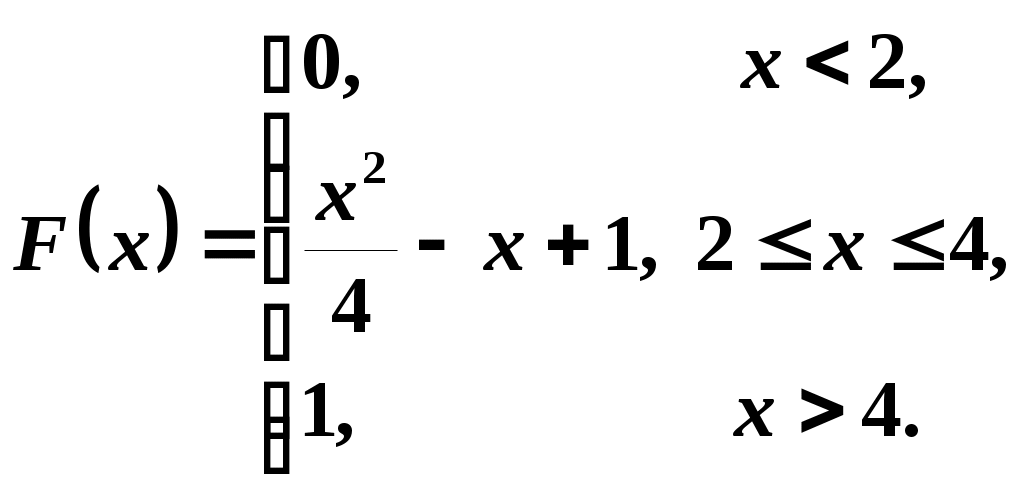
Требуется найти: функцию плотности распределения вероятности и среднее квадратичное отклонение .
.
4. Вероятность попадания в цель при каждом выстреле равна 0,3. Найти математическое ожидание и дисперсию случайной величиныХ – числа попаданий при 40 выстрелах.
5. Случайная ошибка измерительного прибора подчинена нормальному закону распределения с дисперсией 36 . Систематическая ошибка отсутствует. Определить вероятность того, что ошибка измерения по модулю не превзойдет величины 10 мк.
Вариант 19
1. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте – 0,3. Составить закон распределения и функцию распределения случайной величины X – числа отказавших элементов в одном опыте.
2. Случайная величина X задана таблицей распределения:
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Плотность распределения случайной величины задана функцией:
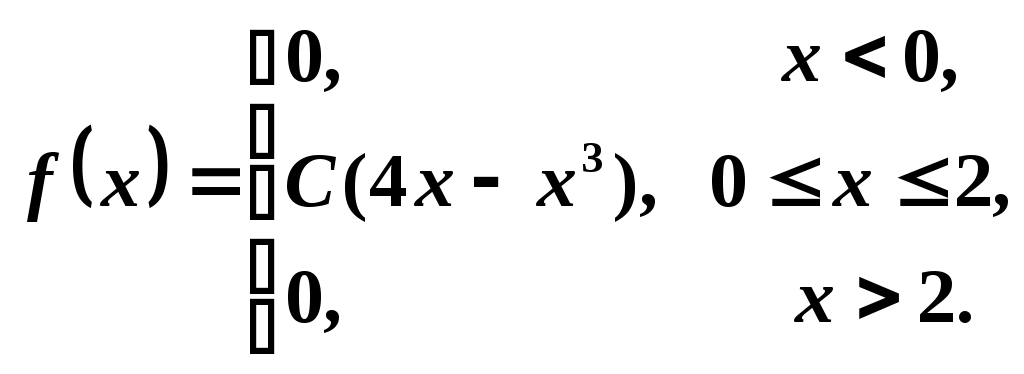 .
.
Найти: параметр C, математическое ожидание M(X), дисперсию D(X).
4. Найти математическое ожидание и дисперсию случайной величины X – числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, причем, вероятность выигрыша по одному билету равна 0,03.
5. Определить среднее квадратическое отклонение ошибки прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и не превосходят по модулю величины 15 м с вероятностью 0,7.
Вариант 20
1. Вероятность попадания бомбы в цель равна 0,4. По цели одиночно сбрасывается 3 бомбы. Найти закон и функцию распределения случайной величины X – числа попаданий бомб в цель.
2. Случайная величина X задана таблицей распределения:
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Плотность распределения случайной величины задана функцией
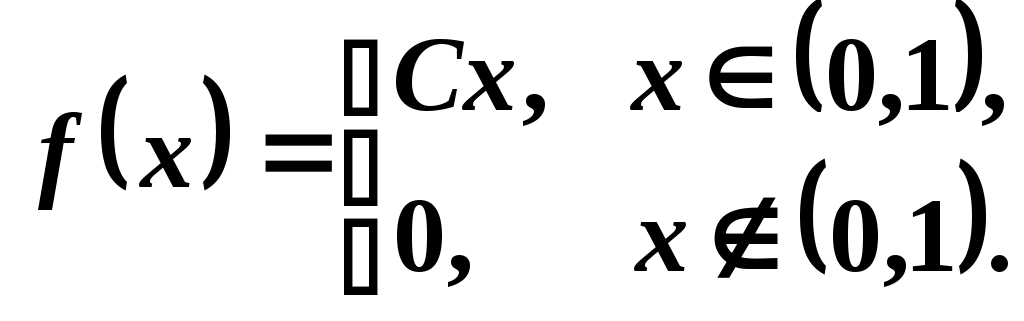 .
.
Найти: параметр C, математическое ожидание M(X), дисперсию D(X), функцию распределения F(x).
4. В лаборатории работают 20 независимых приборов. Вероятность того, что в данный момент прибор работает – 0,7. Найти математическое ожидание и дисперсию числа работающих в данный момент приборов.
5. Производится взвешивание продукта без систематических погрешностей. Случайные погрешности подчинены нормальному закону с дисперсией
25. Найти вероятность того, что взвешивание произведено с погрешностью не превосходящей по абсолютной величине 8 г.
Вариант 21
1. В урне находится четыре шара с номерами 1, 2, 3, 4. Вынули два шара. Построить ряд распределения и функцию распределения случайной величины X – суммы номеров вынутых шаров.
2. В урне находятся 2 белых и 3 черных шара. Последовательно вынимают 3 шара без возвращения. Построить ряд распределения и найти дисперсию случайной величины X — числа вынутых белых шаров.
3. Случайная величина X задана дифференциальной функцией распределения: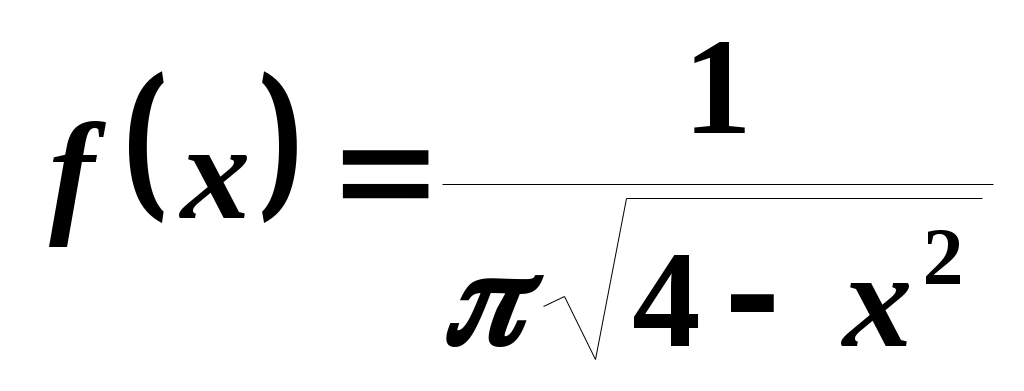 при
при 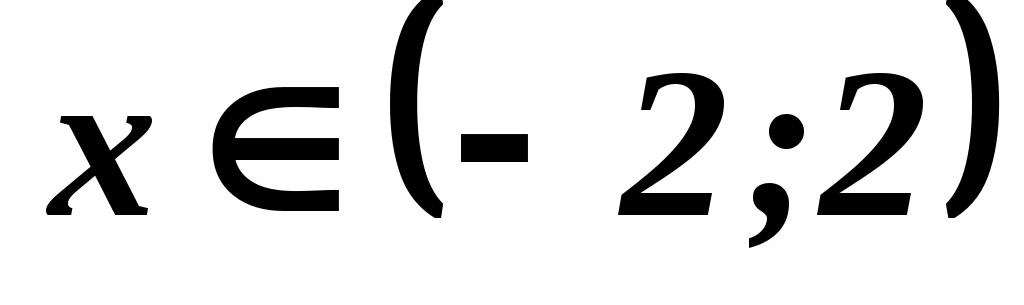 и
и 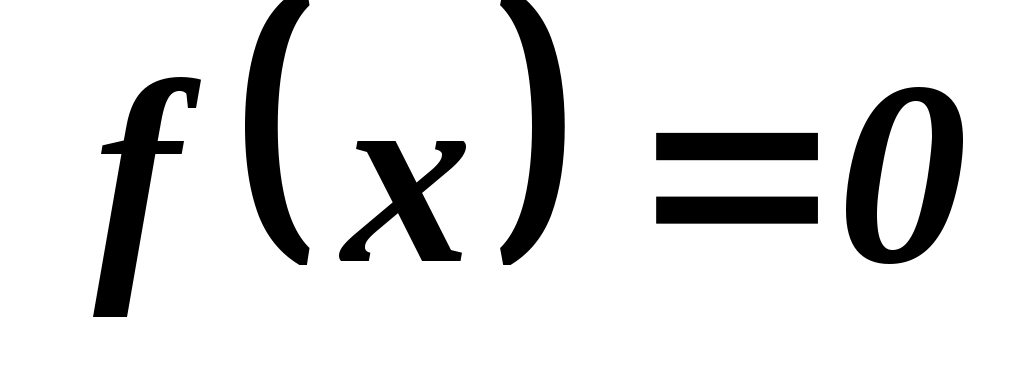 вне этого интервала. Найти M(X), интегральную функцию F(x), дисперсию D(x). Что вероятнее: выполнение неравенства X<1 или X>1?
вне этого интервала. Найти M(X), интегральную функцию F(x), дисперсию D(x). Что вероятнее: выполнение неравенства X<1 или X>1?
4. Найти математическое ожидание дискретной случайной величины X – числа таких бросаний 4 игральных костей, в каждом их которых на двух костях появится по два очка. Общее число бросаний равно 10.
5. Коробки с конфетами упаковываются автоматически: их средняя масса равна 1,08 кг. Найти среднее квадратическое отклонение, если 6 % коробок имеют массу меньше 1 кг. (Масса распределена по нормальному закону.)
Вариант 22
1. Производятся последовательные независимые испытания четырех приборов на надежность. Каждый следующий прибор испытывается только тогда, когда предыдущий оказался надежным. Написать ряд и функцию распределения случайной величины X – числа испытанных приборов, если вероятность выдержать испытания для любого из них равна 0,9.
2. Монету бросают 2 раза. Написать ряд распределения и найти дисперсию случайной величины X – отношения числа выпадений решетки к числу выпадений герба.
3. Плотность вероятности случайной величины X имеет вид:
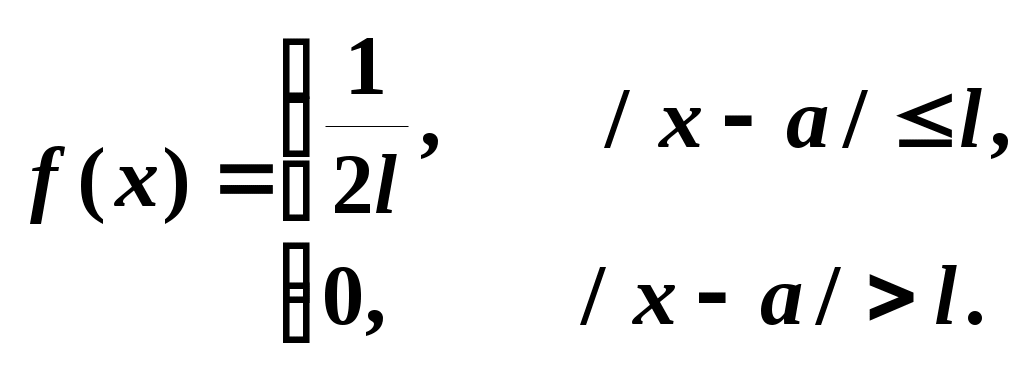
Найти математическое ожидание M(X), интегральную функцию F(x), дисперсию D(x).
4. Устройство состоит из 4 элементов. Вероятность отказа любого элемента за время опыта равна 0,2. Найти математическое ожидание числа таких опытов, в каждом из которых откажет ровно
2. Случайная величина X задана таблицей распределения:
| X | -2 | 1 | 2 |
| P | A | 0,3 | 0,2 |
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Случайная величина X задана дифференциальной функцией распределения
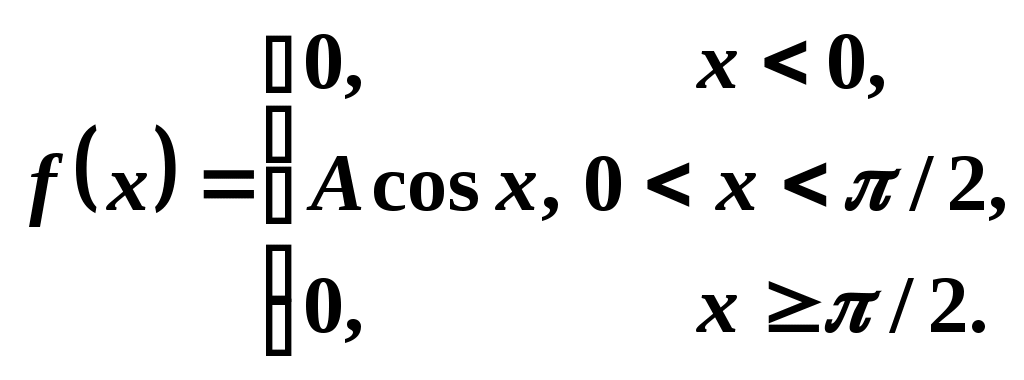
Требуется найти параметр A, математическое ожидание M(X), дисперсию D(X), функцию распределения F(x).
4. Вероятность промаха в цель равна 0,2. Случайная величина X – число попаданий при 40 выстрелах. Найти дисперсию этой случайной величины.
5. Дальномерное устройство измеряет дальность до цели с ошибкой, подчиненной нормальному закону распределения. Среднее квадратическое отклонение ошибки равно 6 м, систематической ошибки нет. Определить вероятность того, что отклонение измеренного значения дальности от истинного не превзойдет значения 5 м.
Вариант 15
1. Вероятность изготовления на автоматическом станке стандартной детали равна 0,7. Написать ряд и функцию распределения случайной величины Х –числа бракованных деталей среди трех наудачу выбранных.
2. Случайная величина X задана таблицей распределения:
| X | 1 | 2 | 4 |
| P | A | 0,4 | 0,2 |
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Плотность распределения случайной величины задана функцией:
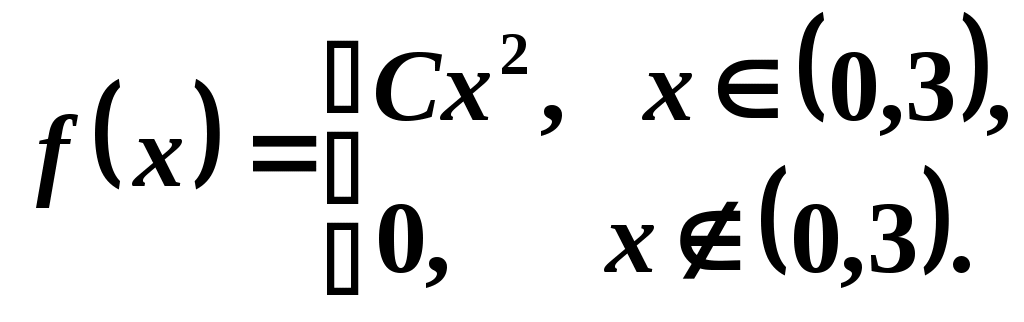 .
.Найти: параметр C, математическое ожидание M(X), дисперсию D(X), функцию распределения F(x)
.
4. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте 0,2. Найти дисперсию случайной величиныХ – числа отказавших элементов в одном опыте.
5. Контролируемая длина детали распределена по нормальному закону и имеет математическое ожидание 25 см. Вероятность того, что длина изготовленной детали окажется в пределах (10, 18) равна 0,45. Найти вероятность того, что длина изготовленной детали окажется в пределах (32, 40).
Вариант 16
-
В партии хлопка 70 % длинных волокон. Построить ряд и функцию распределения числа длинных волокон среди трех отобранных. -
Случайная величина X задана таблицей распределения:
| X | -2 | 0 | 1 |
| P | A | 0,1 | 0,3 |
Найти параметр A, математическое ожидание M(X), дисперсию.
3. Случайная величина X задана дифференциальной функцией распределения
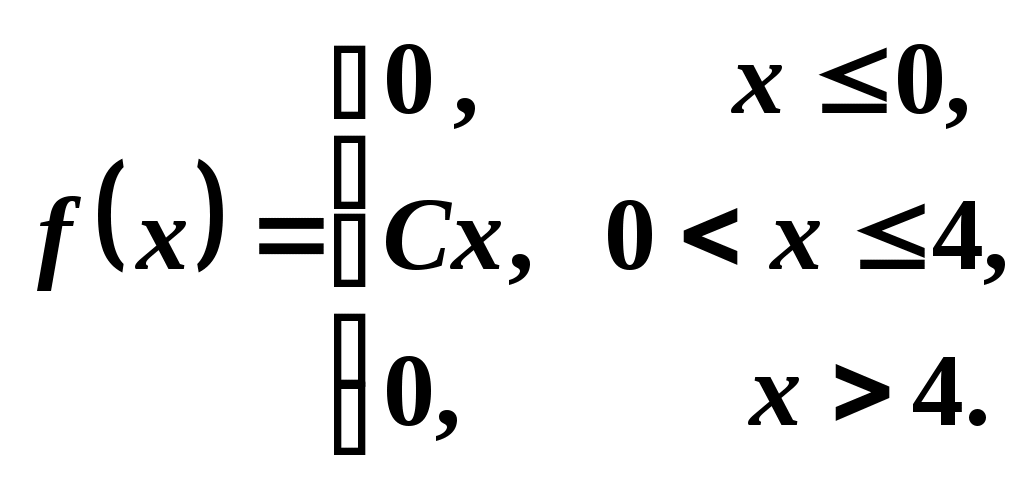 .
.Требуется: найти параметр C, интегральную функцию распределения, вероятность
4. Коммутатор учреждения обслуживает 50 абонентов. Вероятность того, что в течение одной минуты абонент позвонит, равна 0,15. Случайная величина X – число абонентов, позвонивших в течение минуты. Найти математическое ожидание и дисперсию.
5. Вертолет производит одиночное бомбометание по автостраде шириной 16 м, заходя на цель вдоль автострады и прицеливаясь по ее центральной линии. Среднее квадратическое отклонение в боковом направлении равно 20 м. Найти вероятность попадания в цель, если отсутствует систематическая ошибка, а случайная ошибка распределена по нормальному закону.
Вариант 17
1. Монету бросают 3 раза. Найти ряд и функцию распределения случайной величины X – числа выпадений решетки.
2. Случайная величина X задана таблицей распределения:
| X | 1 | 2 | 5 |
| P | 0,4 | А | 0,1 |
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Случайная величина X задана дифференциальной функцией распределения:
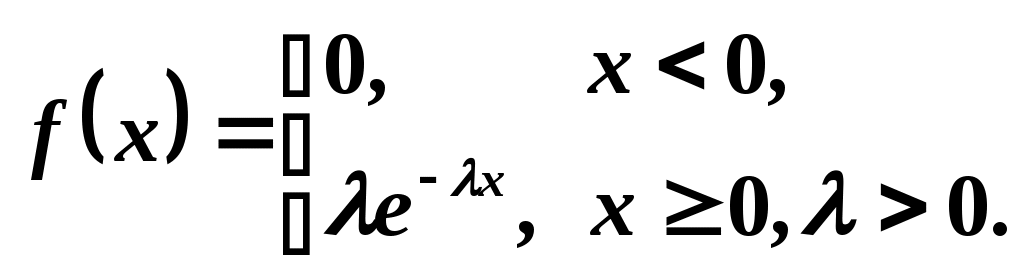 .
.Найти F(x), математическое ожидание M(X). Найти вероятность того, что X примет значение большее, чем её математическое ожидание.
4. Батарея дала 20 выстрелов по объекту. Вероятность попадания в каждом выстреле 0,6. Найти математическое ожидание и дисперсию числа попаданий.
5. Измерительный прибор имеет среднюю квадратическую ошибку 24 м и не имеет систематической ошибки. Найти вероятность того, что ошибка измерения окажется в пределах 8 м.
Вариант 18
1. Игральную кость бросают 3 раза. Написать ряд распределения и функцию распределения случайной величины X — числа выпадения пятерки.
2. Случайная величина X задана таблицей распределения:
| X | -1 | 1 | 2 |
| P | 0,2 | А | 0,3 |
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Случайная величина задана интегральной функцией распределения:
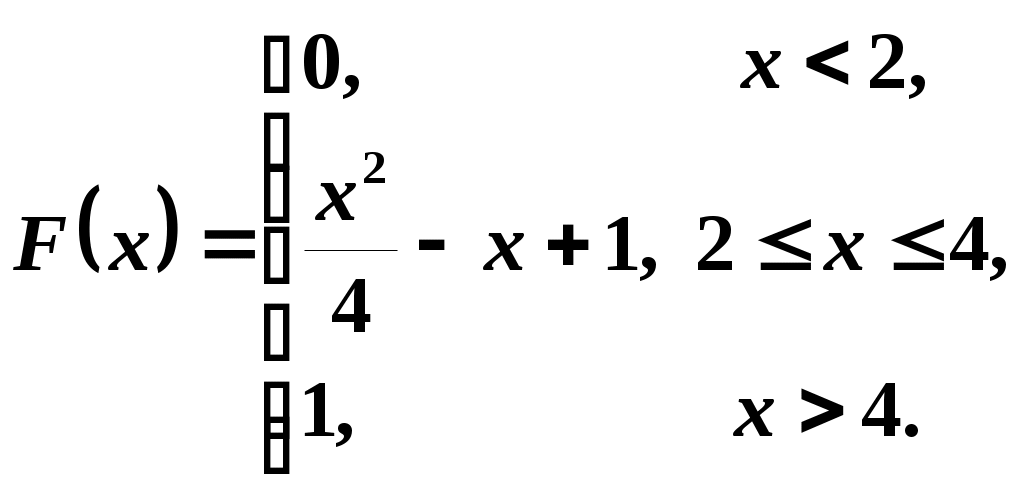
Требуется найти: функцию плотности распределения вероятности и среднее квадратичное отклонение
4. Вероятность попадания в цель при каждом выстреле равна 0,3. Найти математическое ожидание и дисперсию случайной величиныХ – числа попаданий при 40 выстрелах.
5. Случайная ошибка измерительного прибора подчинена нормальному закону распределения с дисперсией 36 . Систематическая ошибка отсутствует. Определить вероятность того, что ошибка измерения по модулю не превзойдет величины 10 мк.
Вариант 19
1. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте – 0,3. Составить закон распределения и функцию распределения случайной величины X – числа отказавших элементов в одном опыте.
2. Случайная величина X задана таблицей распределения:
| X | -2 | -1 | 2 |
| P | 0,1 | А | 0,3 |
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Плотность распределения случайной величины задана функцией:
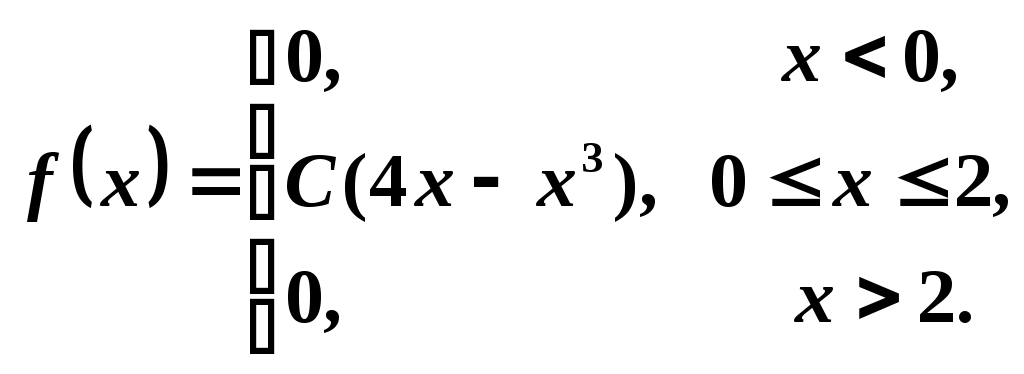 .
.Найти: параметр C, математическое ожидание M(X), дисперсию D(X).
4. Найти математическое ожидание и дисперсию случайной величины X – числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, причем, вероятность выигрыша по одному билету равна 0,03.
5. Определить среднее квадратическое отклонение ошибки прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и не превосходят по модулю величины 15 м с вероятностью 0,7.
Вариант 20
1. Вероятность попадания бомбы в цель равна 0,4. По цели одиночно сбрасывается 3 бомбы. Найти закон и функцию распределения случайной величины X – числа попаданий бомб в цель.
2. Случайная величина X задана таблицей распределения:
| X | -2 | 1 | 2 |
| P | 0,4 | 0,1 | А |
Найти параметр A, математическое ожидание M(X), дисперсию D(X).
3. Плотность распределения случайной величины задана функцией
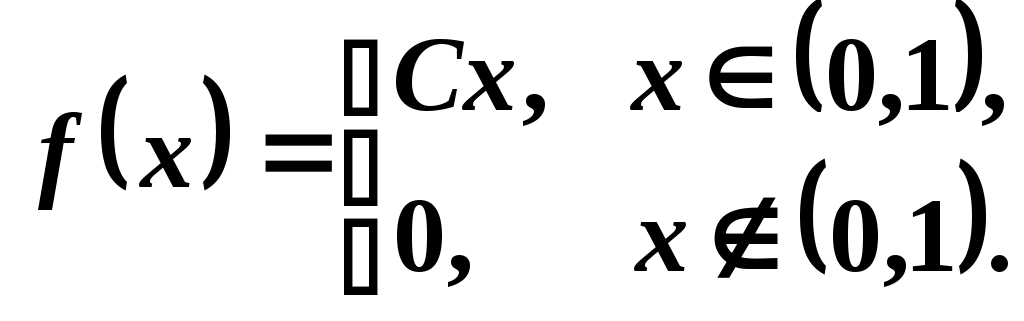 .
.Найти: параметр C, математическое ожидание M(X), дисперсию D(X), функцию распределения F(x).
4. В лаборатории работают 20 независимых приборов. Вероятность того, что в данный момент прибор работает – 0,7. Найти математическое ожидание и дисперсию числа работающих в данный момент приборов.
5. Производится взвешивание продукта без систематических погрешностей. Случайные погрешности подчинены нормальному закону с дисперсией
25. Найти вероятность того, что взвешивание произведено с погрешностью не превосходящей по абсолютной величине 8 г.
Вариант 21
1. В урне находится четыре шара с номерами 1, 2, 3, 4. Вынули два шара. Построить ряд распределения и функцию распределения случайной величины X – суммы номеров вынутых шаров.
2. В урне находятся 2 белых и 3 черных шара. Последовательно вынимают 3 шара без возвращения. Построить ряд распределения и найти дисперсию случайной величины X — числа вынутых белых шаров.
3. Случайная величина X задана дифференциальной функцией распределения:
4. Найти математическое ожидание дискретной случайной величины X – числа таких бросаний 4 игральных костей, в каждом их которых на двух костях появится по два очка. Общее число бросаний равно 10.
5. Коробки с конфетами упаковываются автоматически: их средняя масса равна 1,08 кг. Найти среднее квадратическое отклонение, если 6 % коробок имеют массу меньше 1 кг. (Масса распределена по нормальному закону.)
Вариант 22
1. Производятся последовательные независимые испытания четырех приборов на надежность. Каждый следующий прибор испытывается только тогда, когда предыдущий оказался надежным. Написать ряд и функцию распределения случайной величины X – числа испытанных приборов, если вероятность выдержать испытания для любого из них равна 0,9.
2. Монету бросают 2 раза. Написать ряд распределения и найти дисперсию случайной величины X – отношения числа выпадений решетки к числу выпадений герба.
3. Плотность вероятности случайной величины X имеет вид:
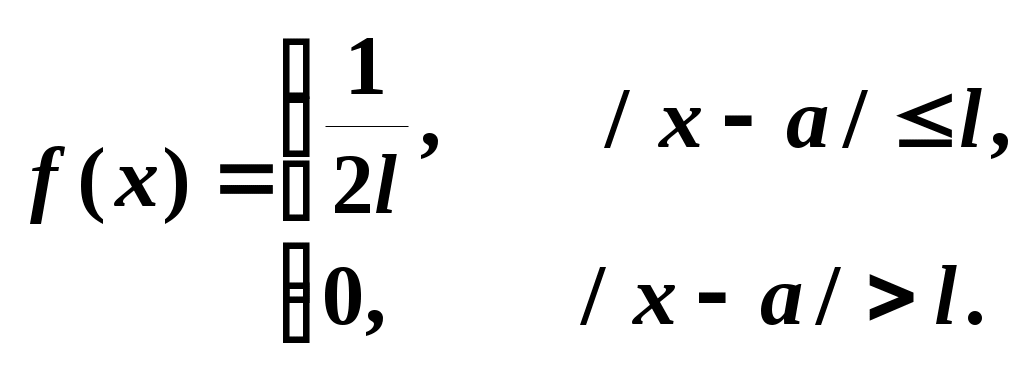
Найти математическое ожидание M(X), интегральную функцию F(x), дисперсию D(x).
4. Устройство состоит из 4 элементов. Вероятность отказа любого элемента за время опыта равна 0,2. Найти математическое ожидание числа таких опытов, в каждом из которых откажет ровно