ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 184
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Требуется при уровне значимости 0,05 установить значимо или незначимо различаются средние результаты анализов, в предположении, что они распределены нормально.
Вариант 10
1. Для выборки: 3; 2; 4; 3; 5; 4; 2; 3; 6; 2; построить полигон относительных частот.
2. По выборке объема 51 найдены средняя выборочная 4 и среднее значение квадрата количественного признака 20. Найти выборочную и исправленную выборочную дисперсии.
3. По данным 20 независимых равноточных измерений некоторой физической величины найдены среднее значение результатов измерений 51,5 и исправленная дисперсия 9. Оценить: истинное значение измеряемой величины с надежностью
.4. По выборке объема n = 62, извлеченной из нормальной двухмерной генеральной совокупности (X,Y), найден выборочный коэффициент корреляции
. Требуется при уровне значимости 0,05 проверить нулевую гипотезу о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе 
.Вариант 11
1. По данному распределению интервальной выборки построить гистограмму относительных частот.
-
-
0-2
2-4
4-6
6-8
8-10
1
2
4
2
1
2. Найти несмещенную оценку генеральной средней по данному распределению выборки.
-
4
7
8
10
20
25
40
15
3. Найти границы, в которых с надежностью 0,95 заключено математическое ожидание нормально распределенного признака генеральной совокупности, если выборочная средняя равна 3, а исправленная дисперсия выборки равна 6,25 и n = 25.
4. Определить коррелированы ли два нормально распределенные количественных признака X и Y по выборке объема n=100, извлеченной из генеральной совокупности (X,Y), если выборочный коэффициент корреляции
.Вариант 12
1. По данному распределению выборки
-
1
2
6
3
4
2
1
3
9
1
найти и построить эмпирическую функцию распределения.
2. Известно, что дисперсия некоторого количественного признака X, полученная по данным выборки объема n=100, равна 6,25. Другой количественный признак Y связан с X зависимостью Y=3X+400. Найти выборочную и исправленную дисперсии Y.
3. Среди 200 деталей, отобранных из партии в 1000 штук, 10 деталей оказались нестандартными. Найти границы, в которых с вероятностью 0,9545, заключена доля нестандартных деталей всей партии. Каким должен быть объем выборки, чтобы те же границы гарантировать с вероятностью 0,9965.
4. Двумя датчиками фиксированы значения одного параметра. Получены следующие результаты:
-
10
12
14
11
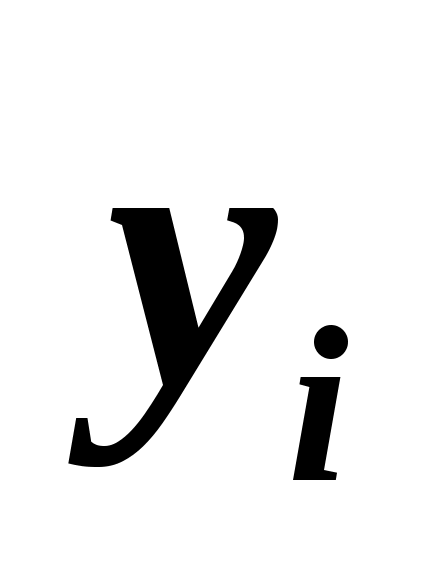
11
13
10
12
1 2 3 4 5
В предположении, что результаты измерений распределены нормально и выборки независимы, можно ли считать, что оба датчика обеспечивают одинаковую точность, если принять уровень значимости a=0,05.
Вариант 13
1. По данному распределению выборки построить полигон частот и эмпирическую функцию распределения
-
xi
3
5
7
9
Ni
1
2
4
3
2. Найти выборочную и исправленную выборочную дисперсии по данному распределению выборки
-
Xi
15
19
21
23
Ni
10
30
40
20
3. Найти доверительный интервал для оценки с надежностью 0,99 неизвестного математического ожидания
нормально распределенного признака Х, если по данным десяти равноточных измерений получено среднее значение результатов измерений 30 и исправленное среднее квадратическое отклонение s = 6.4. Определить являются ли коррелированными нормально распределенные количественные признаки X, Y по выборке объема n = 63, извлеченной из двумерной генеральной совокупности (X,Y), если выборочный коэффициент корреляции
, а уровень значимости считать равным 0,05.Вариант 14
1. По данному распределению интервальной выборки построить гистограмму относительных частот и эмпирическую функцию распределения
-
xi - xi+1
1-3
3-5
5-7
7-9
Ni
1
4
3
2
2. Найти смещенную и несмещенную оценки дисперсии генеральной совокупности по данному распределению выборки:
-
xi
10
12
15
18
ni
25
30
35
10
3. В 400 испытаниях, в каждом из которых вероятность появления события A одинакова и неизвестна, событие A появилось 250 раз. Найти доверительный интервал, покрывающий неизвестную вероятность с надежностью 0,975.
4. Показатели физической активности группы из пяти человек до и после санаторного лечения соответственно следующие:
| xi | 80 | 70 | 50 | 75 | 55 |
| yi | 80 | 65 | 60 | 70 | 60 |
Требуется при уровне значимости 0,01 установить значимо или незначимо увеличилась физическая активность испытуемых в предположении, что показатель имеет нормальное распределение.
Вариант 15
1. По данной выборке построить полигон частот и эмпирическую функцию распределения
10, 6, 8, 9, 5, 6, 8, 10, 5, 7.
2. Среднее выборочное значение признака Х равно 10, а среднее значение квадратаХ, полученное по той же выборке объема 50 равно 104. Найти смещенную оценку генеральной дисперсии этого признака.
3. По данным о продолжительности 100 телефонных разговоров, отобранных по схеме собственно случайной бесповторной выборки, найдено, что доля разговоров, превышающих 8 минут равна 0,2. Найти границы, в которых с вероятностью 0,98 заключена доля таких разговоров на всей телефонной станции.
4. Определить, являются ли коррелированными нормально распределенные количественные признаки X, Y, если по выборке объема n=102, извлеченной из двумерной генеральной совокупности (X,Y), получен выборочный коэффициент корреляции
. (Принять уровень значимости равным 0,01).
Вариант 16
1. По данному распределению выборки построить полигон относительных частот и эмпирическую функцию распределения
-
xi
2
4
6
8
ni
10
20
40
30
2. По данным измерения некоторой величины одним прибором (без систематических ошибок) получена выборка: 9, 11, 13, 15. Найти выборочную и исправленную дисперсии ошибок прибора.
3. По результатам обработки 100 расчетных счетов мелких вкладчиков получены среднее выборочное значение размера вклада, равное 3,4 тысяч рублей и выборочное значение дисперсии размера вклада 1,8. Найти границы, в которых с вероятностью 0,975 заключен средний вклад во всей совокупности, если выборка случайная, бесповторная и осуществлена из 2000 счетов (предполагается, что величина вклада распределена по нормальному закону).
4. Двумя методами в одном и том же порядке определено содержание некоторого вещества в пяти пробах грунта. Результаты первого и второго методов (в процентах к каждой пробе) соответственно следующие:
| xi | 11 | 14 | 17 | 13 | 10 |
| yi | 12 | 13 | 16 | 13 | 11 |
Требуется при уровне значимости 0,05 установить значимо или незначимо различаются средние результаты анализов, в предположении, что они распределены нормально.
Вариант 17
1. По данной выборке построить полигон относительных частот и эмпирическую функцию распределения
1, 3, 5, 1, 3, 7, 3, 1, 5, 7, 4, 1, 5, 7, 3, 7, 1, 3, 6, 5.
2. Найти несмещенные оценки генеральной средней и генеральной дисперсии по данному распределению выборки: