Файл: Курсовая работа по дисциплине Математические методы.doc

Содержание с.

Введение

Курсовая работа по дисциплине «Математические методы» предусмотрена программой по специальности 230105 «Программное обеспечение вычислительной техники и автоматизированных систем».

Курсовая работа – это самостоятельная учебная научно-методическая работа, выполняемая под руководством преподавателя по общенаучным и специальным предметам учебного плана. Имеет целью развитие навыков самостоятельной творческой работы, овладение методами современных научных исследований, углублённое изучение какого-либо вопроса, темы, раздела учебной дисциплины [1].

Основной целью курсовой работы является применение задачи линейного программирования в реальных жизненных ситуациях и такие задачи как:

• 
  решение задачи линейного программирования;
  
• 
  закрепление полученных теоретических знаний и практические умений;
  
• 
  формирование умений применять теоретические знания при решении поставленных вопросов.
  

Курсовая работы была выполнена по результатам практики по профилю специальности, которая была пройдена в Открытом Акционерном Обществе «Нефтекамский автомобильный завод»(ОАО «НефАЗ»), цехе №8 «Сборки, сварки и покраски прицепов, полуприцепов и цистерн».

Для раскрытия темы курсовой работы необходимо выполнить анализ предметной области, составить постановку задачи, составить математическую модель, описать методы решения задач, выбрать и описать программные средства, решить задачи линейного программирования и проанализировать полученные результаты.

1 Теоретические основы разрабатываемой темы

1.1 Основные понятия и определения задач линейного программирования

---

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование – является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Линейное программирование – основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.

Задача линейного программирования – это выбор из множества допустимых планов наиболее выгодного (оптимального).

Каждая задача линейного программирования включает в себя целевую функцию, систему ограничений и допустимый(оптимальный) план, условие и др.

Целевая функция – это функция, связывающая цель (оптимизируемую переменную) с управляемыми переменными в задаче оптимизации.

В широком смысле целевая функция есть математическое выражение некоторого критерия качества одного объекта(решения, процесса и т.д.) в сравнении с другим. Примером критерия в теории статистических решений является среднеквадратический критерий точности аппроксимации. Цель – найти такие оценки, при которых целевая функция достигает максимума (минимума).

Система ограничений – это совокупность ограничений, которым целевая функция должна удовлетворять в ходе всего решения задачи. Систему ограничений накладывают непосредственно при создании самой задачи линейного программирования.

Базисные переменные(БП) –

Свободные члены(СЧ) –

Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений.

Каждая совокупность значений переменных, которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. [2]

1.2 Методы решения задач линейного программирования

---

Математическое моделирование в исследовании операций является, с одной стороны, очень важным и сложным, а с другой — практически не поддающимся научной формализации процессом. Заметим, что неоднократно предпринимавшиеся попытки выделить общие принципы создания математических моделей приводили либо к декларированию рекомендаций самого общего характера, трудно приложимых для решения конкретных проблем, либо, наоборот, к появлению рецептов, применимых в действительности только к узкому кругу задач. Поэтому более полезным представляется знакомство с техникой математического моделирования на конкретных примерах. [3]

Задачи линейного программирования можно решить следующими методами:

• 
  алгоритмом Флойда;
  
• 
  алгоритм Дейкстры на графах;
  
• 
  графический метод;
  
• 
  метод симплекс-таблиц и др.
  

Алгоритм решения задач линейного программирования методом Дейкстры на графах.

В простейшей реализации для хранения чисел d[i] можно использовать массив чисел, а для хранения принадлежности элемента множеству U — массив булевых переменных.

В начале алгоритма расстояние для начальной вершины полагается равным нулю, а все остальные расстояния заполняются большим положительным числом (большим максимального возможного пути в графе). Массив флагов заполняется нулями. Затем запускается основной цикл.

На каждом шаге цикла необходимо найти вершину U с минимальным расстоянием и флагом равным нулю. Затем нужно установить в ней флаг в 1 и проверяем все соседние с ней вершины U. Если расстояние больше, чем сумма расстояния до текущей вершины и длины ребра, то необходимо уменьшить его. Цикл завершается, когда флаги всех вершин становятся равны 1, либо когда у всех вершин c флагом 0 . Последний случай возможен тогда и только тогда, когда граф G не связан. [4]

Способом решения задач линейного программирования графическим методом.

Графический метод решения задачи линейного программирования основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.

---

Пусть задача линейного программирования задана в двумерном пространстве, то есть ограничения содержат две переменные.

Минимальное значение функции определено формулой (1).

(1)

Ограничения представлены формулами (2) и (3).

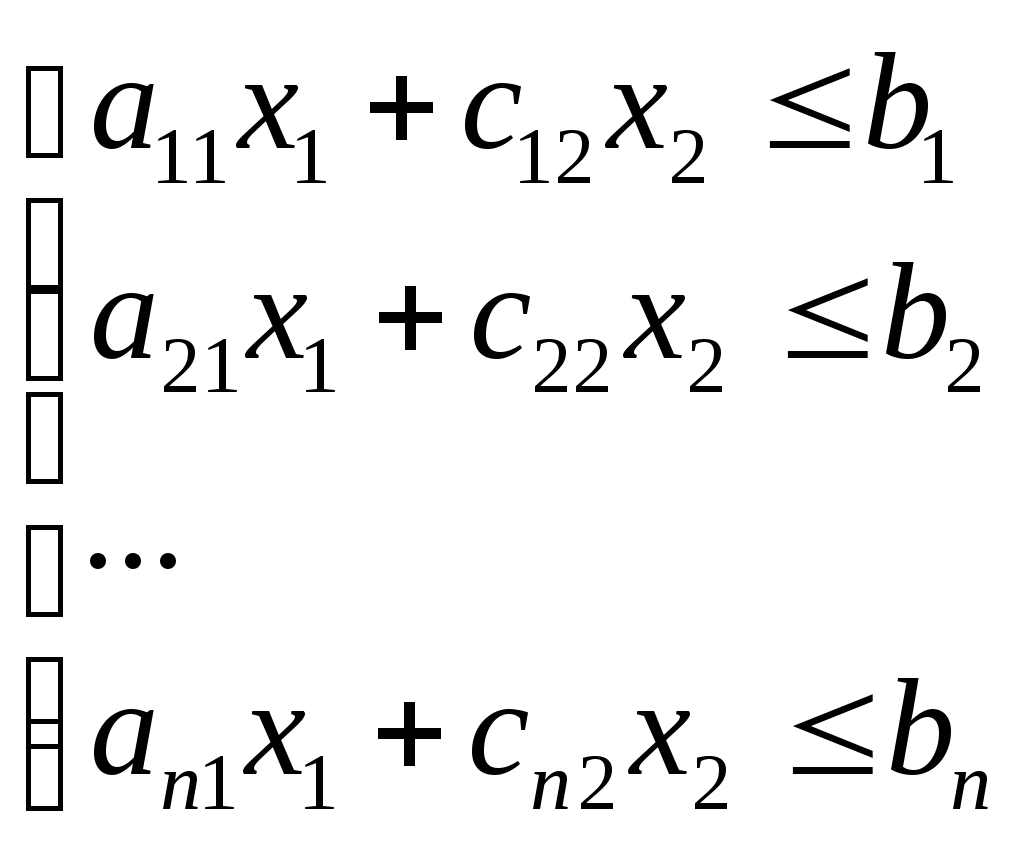(2)

и

(3)

Пусть система (2) при условии (3) совместна. Каждое из неравенств из систем (2) и (3) определяет полуплоскость с граничными прямыми представлено формулой(4):

(4)

Линейная функция (1) при фиксированных значениях Z является уравнением прямой линии:

Необходимо построить многоугольник решений системы ограничений (2) и график линейной функции (1) при Z=0. Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию:

Найти точку многоугольника решений, в которой прямая опорная и функция Z при этом достигает минимума.

Значения уменьшаются в направлении вектора , поэтому прямую Z=0 необходимо передвигать параллельно самой себе в направлении вектора N.

Если многоугольник решений ограничен, то прямая дважды становится опорной по отношению к многоугольнику решений (в точках B и E), причём минимальное значение принимает в точке E. Координаты точки необходимо найти, решая систему уравнений прямых DE и EF.

Если же многоугольник решений представляет собой неограниченную многоугольную область, то возможны два случая.

Случай 1. Прямая , передвигаясь в направлении вектора N или противоположно ему, постоянно пересекает многоугольник решений и ни в какой точке не является опорной к нему. В этом случае линейная функция не ограничена на многоугольнике решений как сверху, так и снизу.

Случай 2. Прямая, передвигаясь, всё же становится опорной относительно многоугольника решений. Тогда в зависимости от вида области линейная функция может быть ограниченной сверху и неограниченной снизу, ограниченной снизу и неограниченной сверху, либо ограниченной как снизу, так и сверху.[5]

---

Для решения данной задачи был выбран наиболее известный и широко применяемый на практике для решения задач линейного программирования является симплекс-метод. Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач линейного программирования, он является алгоритмом с экспоненциальной сложностью.

Симплексный метод задач линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает или убывает. [6]

Перед составлением симплекс-таблицы задача должна быть преобразована, система ограничений приведена к допустимому базисному виду, c помощью которого из целевой функции должны быть исключены базисные переменные как показано на рисунке 1.



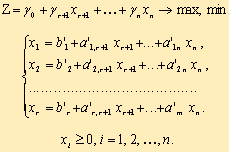
Рисунок 1 – Начальное преобразование системы ограничений

Здесь для определенности записи считается, что в качестве базисных переменных можно взять переменные X1, X2, ..., Xr и что при этом b1, b2,..., br ≥ 0 (соответствующее базисное решение является опорным).

Для составления симплекс-таблицы во всех равенствах в условии задачи члены, содержащие переменные, переносятся в левую часть, свободные оставляются справа, т.е. задача записывается в виде системы равенствкак показано на рисунке 2.


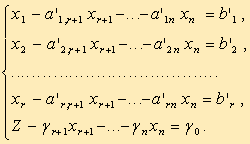
Рисунок 2 – Преобразование системы неравенств

Далее эта система оформляется в виде симплекс-таблиц.

Алгоритм перехода к следующей таблице такой:

• 
  просматривается последняя строка (индексная) таблицы и среди коэффициентов этой строки (исключая столбец свободных членов ) выбирается наименьшее отрицательное число при отыскании max, либо наибольшее положительное при задачи на min. Если такового нет, то исходное базисное решение является оптимальным и данная таблица является последней;
  
• 
  просматривается столбец таблицы, отвечающий выбранному отрицательному (положительному) коэффициенту в последней строке- ключевой столбец, и в этом столбце выбираются положительные коэффициенты. Если таковых нет, то целевая функция неограниченна на области допустимых значений переменных и задача решений не имеет;
  
• 
  среди выбранных коэффициентов столбца выбирается тот, для которого абсолютная величина отношения соответствующего свободного члена (находящегося в столбце свободных членов) к этому элементу минимальна. Этот коэффициент называется разрешающим, а строка в которой он находится ключевой;
  
• 
  в дальнейшем базисная переменная, отвечающая строке разрешающего элемента, должна быть переведена в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных:
  
• 
  разделим каждый элемент ключевой строки (исключая столбец свободных членов) на разрешающий элемент и полученные значения запишем в строку с измененной базисной переменной новой симплекс таблицы.
  
• 
  строка разрешающего элемента делится на этот элемент и полученная строка записывается в новую таблицу на то же место.
  
• 
  в новой таблице все элементы ключевого столбца = 0, кроме разрезающего, он всегда равен 1.
  
• 
  столбец, у которого в ключевой строке имеется 0,в новой таблице будет таким же.
  
• 
  строка, у которой в ключевом столбце имеется 0, в новой таблице будет такой же.
  
• 
  в остальные клетки новой таблицы записывается результат преобразования элементов старой таблицы, как показано на рисунке 3.
  

---