Файл: Курсовая работа по дисциплине Математические методы.doc

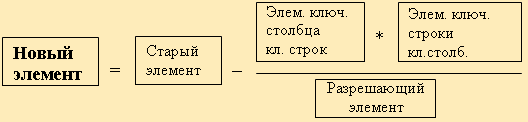
Рисунок 3 – Составление нового элемента в симплекс-таблице

В результате получают новую симплекс-таблицу, отвечающую новому базисному решению.

Теперь следует просмотреть строку целевой функции (индексную), если в ней нет отрицательных значений (в задачи на нахождение максимального значения), либо положительных (в задачи на нахождение минимального значения) кроме стоящего на месте (свободного столбца), то значит, что оптимальное решение получено. В противном случае, переходим к новой симплекс таблице по выше описанному алгоритму. [7]

Для решения задачи данной курсовой работы было выбрано направление задачи по оптимальному распределению средств на предприятии. Оптимальным планом или оптимальным решением задачи линейного программирования является план, при котором значение целевой будет возрастать (убывать).

После анализа собранной информации, была составлена задача линейного программирования по цеху №8 в ОАО «НефАЗ».На покрасочном конвейере, на котором окрашиваются детали. Необходимо покрасить оптимальное количество деталей за одну рабочую смену, чтобы прибыль была максимальной.

Для дальнейшего решения задачи необходимо составить постановку задачи и математическую модель задачи.

2. Практическая часть разрабатываемой темы

2.1 Постановка задачи

Постановка задачи – точная формулировка условий задачи с описанием входной и выходной информации. [5]

На предприятии ОАО «НефАЗ» в цехе №8 «Сборка, сварка и покраска прицепов, полуприцепов и цистерн» для полной покраски детали на конвейере детали необходимо пройти несколько операций в определенных камерах, таких как камера мойки, камера сушки, камера грунтовки и т.д. В каждой камере деталь обрабатывается определенный промежуток времени.

Прибыль от выпущенных деталей и затраты времени на покраску приведены в таблице 1.

В поставленной задаче будет рассмотрен объем выпущенных деталей на конвейере за рабочую смену.

Таблица 1 – Прибыль и затраченное время на покраску детали в часах.

Операции	Наименование деталей
	Адаптер	Заглушка	Втулка	Держатель	Балка
Мойка,час	0,2	0,6	0,8	0,3	0,5
Грунтовка,час	0,5	0,3	0,4	0,6	0,4
Покраска,час	0,7	0,5	0,3	0,2	0,8
Сушка,час	0,8	0,4	0,2	0,3	0,7
Прибыль,руб	700	530	240	450	820

---

Необходимо найти оптимальный план выпуска деталей за одну рабочую смену, при котором прибыль будет максимальной.

Для дальнейшего решения необходимо составить математическую модель к задаче, которая описана в следующем пункте.

2.2 Математическая модель задачи

Модель – это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале

Математическое моделирование – это средство изучения реального объекта, процесса или системы путем их замены математической моделью, более удобной для экспериментального исследования с помощью электронных вычислительных машин. Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи. Математическое моделирование широко применяется в разделе линейного программирования.

Классификация математических моделей:

• 
  линейные модели;
  
• 
  дескриптивные (описательные) модели;
  
• 
  оптимизационные модели;
  
• 
  многокритериальные модели;
  
• 
  игровые модели. [6]
  

Для решения данной задачи была выбрана линейная модель. Основные обозначения для составления математической модели:

• 
  N – множество покрашенных деталей;
  
• 
  Pi – прибыль от каждой детали, iN.
  

Искомые величины задачи:

L – максимальная прибыль за рабочую смену.

Составление математической модели задачи линейного программирования включает в себя:

• 
  выбор переменных задачи;
  
• 
  составление системы ограничений;
  
• 
  выбор целевой функции.
  

Переменными в задаче будут называться величины: адаптер-х1, заглушка-х2, втулка-х3, держатель-х4, балка-х5. Время покрасочного конвейера не должен превышать рабочий лимит смены (8 часов), но так же и не может быть меньше.

Целевой функцией задачи называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.

Системой ограничений задачи называют совокупность уравнений и неравенств описывающих ограниченность ресурсов в рассматриваемой задаче. [7]

С помощью таблицы 1 можно увидеть, сколько времени занимает каждая операция у каждой детали.

---

На покрасочном конвейере, в камере мойки деталей мойка адаптера составляет 0,2 часа, мойка заглушки составляет 0,6 часа, мойка втулки составляет 0,8 часа, мойка держателя составляет 0,3 часа, мойка балки составляет 0,5 часа.

В камере грунтовки деталей грунтовка адаптера составляет 0,5 часа, грунтовка заглушки составляет 0,3 часа, грунтовка втулки составляет 0,4 часа, грунтовка держателя составляет 0,6 часа, грунтовка балки составляет 0,4 часа.

В камере покраски деталей покраска адаптера составляет 0,7 часа, покраска заглушки составляет 0,5 часа, покраска втулки составляет 0,3 часа, покраска держателя составляет 0,2 часа, покраска балки составляет 0,8 часа.

В камере сушки сушка адаптера составляет 0,8 часа, сушка заглушки составляет 0,4 часа, сушка втулки составляет 0,2 часа, сушка держателя составляет 0,3 часа, сушка балки составляет 0,7 часа.

С помощью этих данных систему ограничений можно представить формулой 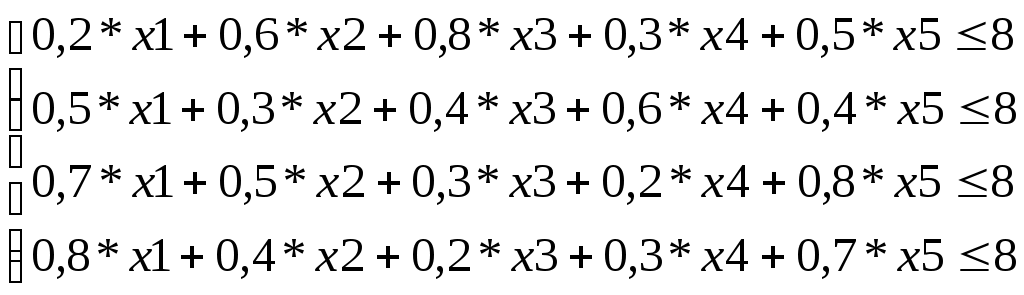(6):

(6)

Количество покрашенных деталей не должно быть отрицательным. Поэтому необходимо задать условия: . Целевая функция задачи представлено формулой (7):

.

Таким образом:

(4)

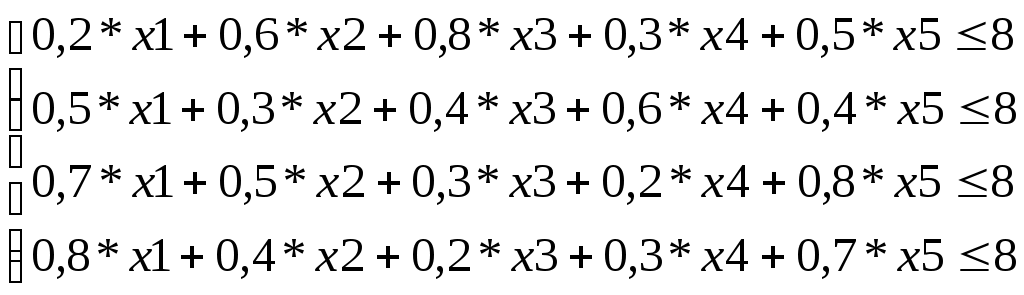(5)

(6)

2.3 Расчетная часть задания, выполненная аналитически

Задача линейного программирования будет решена на нахождения максимума(минимума).

Необходимо найти начальное опорное (абсолютно произвольное) решение для функции L, которое бы удовлетворяло системе наложенных ограничений. Далее, применяя симплекс таблицы, будет получаться решение, при котором значение функции будет, как минимум, не убывать. И так до тех пор, пока не будет достигнуто оптимальное решение, при котором функция достигает своего максимума. Перед применением симплекс таблиц, необходимо преобразовать систему линейных ограничений и рассматриваемую функцию L к вполне определенному виду.

Далее необходимо найти наибольшее значение линейной функции при заданных ограничениях представлены формулами (7) и (8):

---

(7)

(8)

Свободные члены системы ограничений должны быть неотрицательными. Система ограничений должна быть приведена к канонической форме. Т.е. к левой части неравенства первой системы ограничений прибавляем неотрицательную переменную x₆ – необходимо преобразовать первое неравенство в равенство. К левой части неравенства второй системы ограничений прибавляем неотрицательную переменную x₇ – необходимо преобразовать второе неравенство в равенство. К левой части неравенства третьей системы ограничений прибавляем неотрицательную переменную x₈ - необходимо преобразовать третье неравенство в равенство. К левой части неравенства четвертой системы ограничений прибавляем неотрицательную переменную x₉ – необходимо преобразовать четвертое неравенство в равенство. Преобразованную систему можно представить формулой 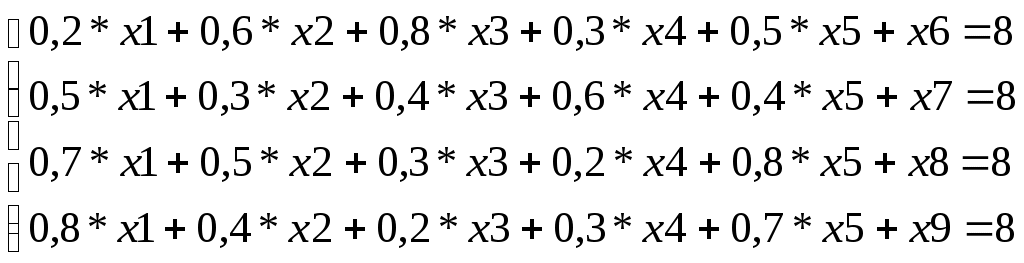(9):

(9)

Переменная x₆ входит в первое уравнение с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. x₆ – базисная переменная. Переменная x₇ входит во второе уравнение с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. x₇ – базисная переменная. Переменная x₈ входит в третье уравнение с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. x₈ – базисная переменная. Переменная x₉ входит в четвертое уравнение с коэффициентом 1, а в остальные уравнения системы с коэффициентом ноль, т.е. x₉ – базисная переменная(БП).

Свободные члены(СЧ) в данном случае в каждой строке одинаковые, т.е. в каждой строки свободный член будет равняться 8.

Функция L не должна содержать базисные переменные . Значение функции L для начального решения: L (X

---

_нач) = 0.

При составлении исходной симплекс таблицы, коэффициенты при переменных функции L записываются с противоположными знаками, а свободный член со своим знаком.

Ключевым столбцом будет x5, так как при решении задачи на максимум берется самая наименьшее (наибольшее) число из L строки в данном случае число -820(задача на максимум). Элемент L строки, принадлежащий столбцу свободных членов не рассматривается. Ключевой строкой будет строка х8, так как отношение свободного члена к соответствующему элементу выбранного столбца для третьей строки является наименьшим. Необходимо обратить внимание, что отношение вычисляются только для положительных элементов пятого столбца. Как показано в таблице 1.

Таблица 1 – Первоначальная симплекс-таблица

БП	СЧ	х1	х2	х3	x4	x5	x6	x7	x8	x9
x6	8	0,2	0,6	0,8	0,3	0,5	1	0	0	0
x7	8	0,5	0,3	0,4	0,6	0,4	0	0	0	0
x8	8	0,7	0,5	0,3	0,2	0,8	0	0	1	0
x9	8	0,8	0,4	0,2	0,3	0,7	0	0	0	1
L	0	-700	-530	-240	-450	-820	0	0	0	0

Необходимо построить новую таблицу, заменяется во второй таблице базисную переменную х8 на х5, необходимо разделить элементы первой таблицы первой строки x8 на 0,8. Далее необходимо от элементов первой строки отнимаются

---