ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 80
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
По результатам расчетов строим эпюры перерезывающей силы Qpот веса тележки в различных сечениях балки при x = 0,1l; x = 0,2l … x = 0,5l (рисунок 1.5а).
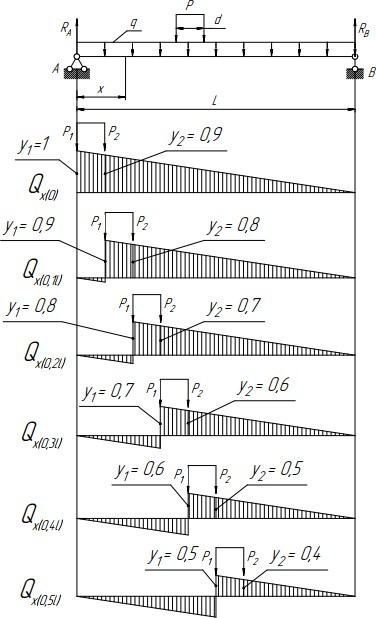
Рисунок 1.4 – линия влияния перерезывающей силы Qx в различных сечениях подкрановой балки.
Определяем перерезывающую силу Qqот действия распределенной нагрузки по формуле:
????????
=???????? − ???????? (1.13)
 2
2Подставляем исходные данные в формулу 1.13 и получим:
При x = 0: ????????
= 0,001 (900∙20 − 900 ∙ 0) = 9 т;
2
При x = 0,1l: ???????? При x = 0,2l: ???????? При x = 0,3l: ????????
= 0,001 (900∙20 − 900 ∙ 2) = 7,2 т;
2
= 0,001 (900∙20 − 900 ∙ 4) = 5,4 т;
2
= 0,001 (900∙20 − 900 ∙ 6) = 3,6 т;
2
При x = 0,4l: ????????
При x = 0,5l: ????????
= 0,001 (900∙20 − 900 ∙ 8) = 1,8 т;
2
= 0,001 (900∙20 − 900 ∙ 10) = 0 т.
2
По результатам расчетов строим эпюры перерезывающей силы Qqот веса тележки в различных сечениях балки при x = 0,1l; x = 0,2l … x = 0,5l (рисунок 1.5б).
Суммарная перерезывающая сила Qp+qот действия сосредоточенной по- движной и распределенных нагрузок будет:
????????+???? = ???????? + ???????? (1.14)
Подставляем исходные данные в формулу 1.14 и получим: При x= 0,1l, ????????+???? = 9,35 + 7,2 = 16,55 т;
При x= 0,2l, ????????+???? = 8,25 + 5,4 = 13,65 т; При x= 0,3l, ????????+???? = 7,15 + 3,6 = 10,75 т; При x = 0,4l, ????????+???? = 6,05 + 1,8 = 7,85 т; При x= 0,5l, ????????+???? = 4,95 + 0 = 4,95 т.
По результатам полученных расчетов строим эпюры суммарной перерезывающей силы Qp+qот действия сосредоточенной подвижной и распределенных нагрузок в различных сечениях балки при x= 0,1l; x= 0,2l… x
= 0,5l(рисунок 1.5в). Ординаты линии влияния перерезывающей силы также, как и опорной реакции, являются безразмерной величиной.
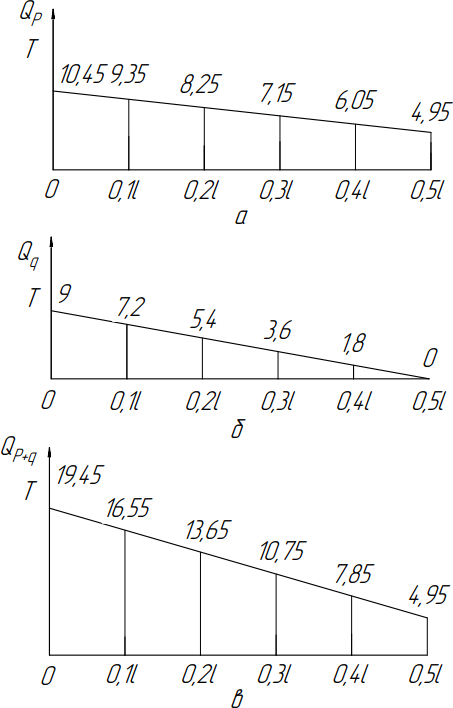
Рисунок 1.5 – эпюры перерезывающей силы в различных сечениях балки: а) Qp
– перерезывающая сила от действия подвижной нагрузки P; б) Qq– перерезывающая сила от действия распределенной нагрузки q; в) Qp+q– суммарная перерезывающая сила.
При проектировании сварных балок необходимо стремиться к минималь- ной площади поперечного сечения F при максимальном моменте инерции J и моменте сопротивления W. Часто применяют сварные балки коробчатого сече- ния (рисунок 2.1), которые хорошо сопротивляются и кручению. Сварка позволяет изготавливать балки высотой до 4 метров и более, а также любой длины. Показателем экономичности сечения является параметр W/F. Чем выше это со- отношение, тем при меньшей массе металла достигается увеличение сопротив- ления профиля на изгиб. Однако принимать чрезмерно тонкие вертикальные стенки опасно из-за возможности потери местной устойчивости. 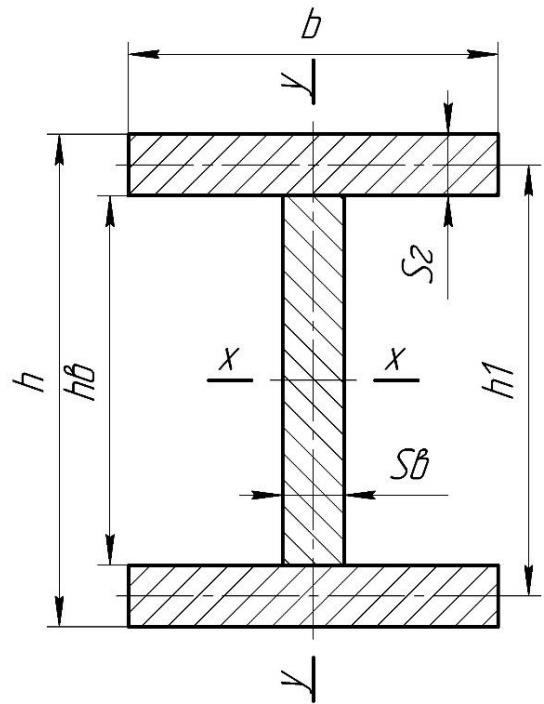 Рисунок 2.1 – схема поперечного сечения двутавровой балки.
Балка должна удовлетворять условиям жесткости, т.е. ее прогиб fmaxот наибольшей нагрузки не должен превышать предельно допускаемый. Обычно в балках данное требование регламентируется нормой жесткости, т.е. отношением fmax/l.В данной работе это соотношение: fmax/l= 1/600. | |||||||
| КР-40461806-15.03.01-13Б-2023 | |||||||
| Изм. | Лист | № докум | Подпись | Дата | | | |
| Разраб | АрбатскийД.В. | | | Литера | Лист | Листов | |
| Пров | | КузьминЕ.В. | | | | 17 | 43 |
| | | | Балкасварная | ВолгГТУМС-328 | |||
| Н.Контр. | КузьминЕ.В. | | | ||||
| Утв | | ЛысакВ.И. | | | | ||
Чтобы удовлетворить требованиям жесткости, балка должна иметь высоту не меннее некоторой предельной величины. Эта минимальная высота балки опре- деляется видом нагружения и допускаемыми напряжениями. Рассмотрим, какова должна быть предельно наименьшая высота балки h, свободно лежащей на двух опорах, если она нагружена равномерно распределенной нагрузкой.
Величина расчетного прогиба равна:
????????????????
= 5
 384
384-
, (2.1)

????∙????
????∙????
где E – модуль упругости, кг/см2; J – момент инерции, см4.
Величина максимального изгибающего момента равна:
 ???? = ????∙????2
???? = ????∙????28
Подставляя значение Mв формулу 2.1, получим:
(2.2)
????????????????
= 5 ∙ ????∙????2

 48 ????∙????
48 ????∙????(2.3)
Величина изгибающего момента может быть выражена как:
???????? = ???????? ∙ ???? (2.4)
Принимая ????max = [????]р получим:
???? = [????]р ∙ ????, (2.5)
где [????]р – допустимое напряжение при растяжении, кг/см2;
W– момент сопротивления, см3.
2∙????
Если расчетное сечение симметрично относительно горизонтальной оси x-x(рисунок 2.1), то момент сопротивления:
???? = , (2.6)
ℎ
Подставив значение Mиз формулы 2.5 в формулу 2.3, получим:
5 [????]р∙????2
откуда
???????????????? =
∙

 24 ????∙ℎ
24 ????∙ℎ, (2.7)
где l/fmax– величина обратная задаваемой нормы жесткости fmax/l.
Высота балки, вычисленная по формуле 8, является наименьшей при за- данных [????].
При нагружения балки сосредоточенной силой P в середине пролета вы- сота балки рассчитывается по формуле:
 ℎ = 1
ℎ = 16
-
????
 ????????????????
????????????????-
????
 ????
????-
???? (2.9)
Если на балку одновременно действуют распределенная и сосредоточен- ная нагрузки, максимальный суммарный прогиб равен:
???? = ????
+ ????
= 5 × ????

× [????]
1 ????

× [????]
× ???? (2.10)
????????????
????????????1
????????????2

 24 ????????????????1
24 ????????????????1× ???? + ×
????×ℎ 6 ????????????????2

 ????×ℎ
????×ℎПри нагружении балки равномерной нагрузкой q по её длине:
 ℎ = 5
ℎ = 524
-
????
 ????????????????
????????????????∙ ???????? ∙ ???? (2.10)
 ????
????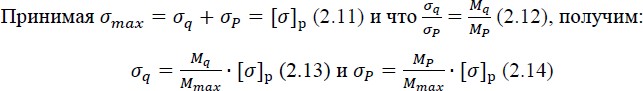
где Mmax– максимальный суммарный изгибающий момент, определяемый по формуле 1.9, тм.
Подставив значения ????q и ????P в формулу для прогиба 10, получим выраже- ние, аналогичное выражениям 8 и 9, отличающееся только величиной числового коэффициента k:

В данной работе применяется сталь 14ГС для которой [????]р = 210 МПа, E = 2·105 МПа.
Подставив исходные данные в формулу 2.16, получим:
???? =
5
 24 ∙
24 ∙45
 94,5
94,51
 + 6 ∙
+ 6 ∙49,5

94,5
= 0,18
Далее подставив полученные результаты в формулу 2.15 получим:
210
 ℎ = 0,18 ∙ 600 ∙ 2 ∙ 105 ∙ 20000 = 2268 мм.
ℎ = 0,18 ∙ 600 ∙ 2 ∙ 105 ∙ 20000 = 2268 мм.С учетом округления принимаем высоту балки h= 2,27 м =2270 мм.
- Определение высоты балки из условий прочности и экономичности
Помимо условий жесткости балка также должна удовлетворять условиям прочности и наименьшего веса, т.е. поперечное сечение должно быть минималь- ным.
Высота балки для двутаврового профиля определяется по следующей формуле:

ℎ = √????Ʃ
????????∙[????????]
(2.17)