ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 93
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
где ????Ʃ – суммарный изгибающий момент балки в опасном сечении, ???????? −
толщина вертикального листа.
При проектировании балки необходимо задать величину Sв т.к. он не известна. Для тяжело нагруженных балок обычно принимают Sв = 10-18мм. В данной работе Sв = 10 мм.
Подставляем исходные данные в формулу 2.17 и получаем
945000000 ℎ = (1,4)√10 ∙ 210
= 939 мм
При выборе высоты балки назначают наибольшую полученную высоту, в данной работе h =1,85 м = 2,27 мм.
Толщину вертикального листа коробчатой балки определяют по следую-щей формуле:Где hв = 0,95h. Подставив значения в формулу 2.18, получаем:
???????? =
√0,95 ∙ 2270
11 = 4,2 ммУчитывая рекомендации принимаем Sв = 10 мм.
Расчет и подбор поперечного сечения балки
Подбор сечения балки начинаем с расчета требуемого момента сопротивления требуемого момента инерции сечения:????тр
= ???? [????????]
= 945000000 = 4500000 см3 (2.19)
210???? = ???? ℎ = 4500000 ∙ 2270 = 5107500000 см4 (2.20)
тр тр 2 2
Вычисляем момент инерции вертикального листа высотой hв и толщиной Sв:
????
????????ℎ3
???? = ????
12
(2.21)
???????? =
10 ∙ (0.95 ∙ 2270)3
12
= 8357322114 ????м4
Далее находим момент инерции двух горизонтальных листов:
????г = ????тр − ????в (2.22)
Подставив числовые значения в формулу 2.22 получим:
????г = 8357322114 − 5107500000 = 3249822114 мм4
По-другому момент инерции двух горизонтальных листов можно выразить как:
1
2
ℎ
????г = 2 [????0 + ????г( 2 )] (2.23)
где J0 – момент инерции горизонтального листа относительно собственной оси, который всегда очень мал и может быть принят равным нулю;
h1 – расстояние между центрами тяжести горизонтальных листов, которое можно принять равным (0,96-0,98) ·h.
h1 = 0,98·2270 = 2225 мм
Из формулы 2.22 находим требуемую площадь сечения одного горизонтального листа:
????г
= 2 ∙ ????г
2
ℎ
1
(2.24)
Подставив числовые значения в формулу 2.23 получаем:
????г
= 2 ∙ 3249822114 = 1312 мм2
22252Размеры пояса Sг и b должны соответствовать ГОСТ 82-70 на сталь широкополосную, из которой рекомендуется изготовлять пояса балок (она дешевле листа, имеет строгие размеры, как по толщине, так и по ширине, не имеет сабле-видности и выпускается длинной до 18м).
Толщину горизонтального пояса можно выбрать по зависимости:
????г = (0,01 … 0,25) ∙ ℎ, (2.25)
Подставив числовые значения в формулу 2.25 получим:
????г = 0,01 ∙ 2270 = 22,7 мм
Ширина пояса равна:
???? = ????г
????г
(2.26)
Подставив числовые значения в формулу 2.26 получим:
???? = 1312 = 58 мм22,7
По ГОСТ 82-70 принимаем Sг = 25 мм и b= 200 мм.
При расчете пояса необходимо выполнить следующие требования:
-
b/Sг = 10-20 (но не более 24), что обеспечит местную устойчивость полоксжатого пояса; лучше, если b/Sг ближе к 20; -
b ≥ 200мм для балок с h ≥ 700 мм; -
в поясах должно содержаться не менее 30% материала сечения балки,для чего
????г = 200 × 25 ≥
????г
????г = ???? × ????г ≥ 70 × 150,95 × 2270 × 10
70 × 15 = 5000 ≥ 4621По ГОСТ 82-70 и с учетом требований выше принимаем Sг = 25 мм и b
=200 мм.
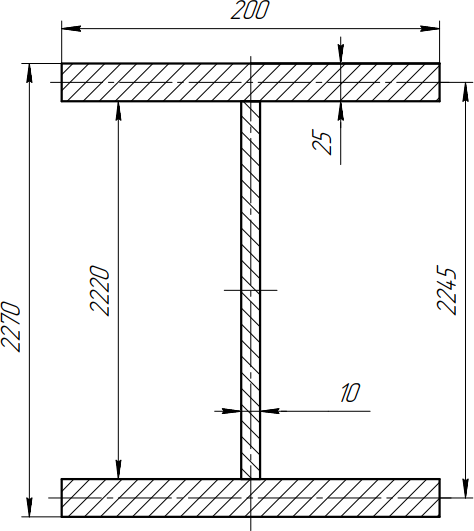
Рисунок 2.2 – поперечное сечение балки
- 1 2 3 4 5 6 7 8 9
Проверка на прочность и экономичность сечения балки
После подбора сечения балки необходимо произвести четыре проверки
-
Проверка по максимальным напряжениям. Напряжение от изгиба должно быть:
???? = ???????????????? ∙ ℎ(2.27)
???? 2
где J– осевой момент инерции подобранного сечения.
Перегруз более 5% недопустим. Недогруз более 5% допускается, если он оправдан, например, выбором высоты из сечения жесткости.
Подставив числовые значения в формулу 2.27 получим:
945000000
???? = 5107500000 ∙2270
2 = 210 МПа ≤ 210 МПа-
Проверка по максимальным касательным напряжениям Касательные напряжения должны быть:
где Qmax– максимальная перерезывающая сила;
S– статический момент полуплощади сечения (симметричного) относи- тельно центра тяжести балки.
Статический момент половины площади балки относительно оси x-xравен
сумме статических моментов отдельных фигур:
где ????ст.г – статический момент горизонтального