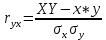ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 44
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
дМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«Северный (Арктический) федеральный университет имени М.В. Ломоносова»
Высшаяшколаэнергетикинефтиигаза
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА
| По дисциплине | Методыанализаданных | |
| На тему | Вариант4 | |
| Выполнил обучающийся: Жеваго Андрей Сергеевич |
| (Ф.И.О.) |
| Направление подготовки / специальность: 13.03.01 «Теплоэнергетика и теплотехника» |
| (код и наименование) |
| Курс: 2 |
| Группа:111113 |
| Руководитель: Зеленина Лариса Ивановна, доцент кафедры высшей и прикладной математики |
| (Ф.И.О. руководителя, должность / уч. степень / звание) |
Отметка о зачете
(отметка прописью) (дата)
Руководитель Л. И. Зеленина
(подпись руководителя) (инициалы, фамилия)
Архангельск 2023
Задания для расчетно-графической работы
ЗАДАЧА 1.
-
Построить по зависимому признаку Y дискретный вариационный ряд, по независимому признаку Х – интервальный вариационный ряд. Построить полигон и гистограмму. -
Оценить статистические характеристики рядов распределения.-
Показатели центра распределения: средняя, мода, медиана -
Показатели вариации признака: размах вариации, дисперсия, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии, коэффициент эксцесса.
-
-
Построить нормальную кривую по эмпирическим и теоретическим данным. На основе одного из критериев согласия Пирсона проверить гипотезу о законе нормального распределения. -
Выполнить статистическую оценку (точечную и интервальную) параметров распределения:-
определить ошибку выборки: стандартную ошибку выборочной средней, ошибку среднего квадратического отклонения, ошибку коэффициента вариации -
оценить достоверность выборочной средней, среднего квадратического отклонения и коэффициент вариации по t-критерию Стьюдента.
-
Выполнить интерпретацию результатов, сделать вывод.
ЗАДАЧА 2.
На основе имеющихся данных выполнить корреляционно – регрессионный анализ.
-
Построить поле корреляции, выдвинуть гипотезу о типе аппроксимирующей функции -
Построить линейную трендовую модель. -
Для построенной модели определить коэффициент корреляции и коэффициент детерминации. -
Для построенной модели дать сравнительную оценку силы связи фактора с результатом с помощью среднего коэффициента эластичности -
Для построенной модели оценить качество построенных моделей с помощью средней ошибки аппроксимации. -
Для построенной модели оценить статистическую значимость параметров регрессии и уравнения регрессии в целом. -
На основе пунктов 2-6 сделать вывод о качестве и точности построенной модели, выполнить прогноз среднего значения показателя Y при уровне значимости α=0,1, если прогнозное значение фактора X составляет 80 % от его максимального значения.
ЛИСТ ДЛЯ ЗАМЕЧАНИЙ
Оглавление
Теоретическая часть 6
Практическая часть 1 11
Практическая часть 2 23
ЗАКЛЮЧЕНИЕ 29
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 30
Теоретическая часть
Вопрос 4
Метод моментов: Этот метод основан на использовании моментов распределения данных для оценки параметров модели.
Моменты — это статистические характеристики данных, такие как среднее значение, дисперсия и т. д.
Для основных видов распределений приведем выражение некоторых моментов через параметры распределения
| Вид распределения | Параметры | Основные моменты |
| Биномиальное распределение | | |
| Закон Пуассона | а | |
| Нормальное распределение | | |
| Равномерное распределение | А, В | |
| Показательное распределение | | |
При заданном виде закона распределения случайной величины X неизвестные параметры этого распределения можно оценить, т.е. выразить как функцию вариант выборки, на основе метода моментов.
Этот метод состоит в том, что приравниваются соответствующие теоретические и эмпирические моменты и из полученных уравнений находятся
оценки параметров. В случае одного параметра в теоретическом распределении для его оценки достаточно составить одно уравнение. Если имеются два параметра в теоретическом распределении, то нужно приравнять соответственно два теоретических и эмпирических момента и т.д.
1. Оценка одного параметра
Пусть задана плотность распределения f (x, ) с одним параметром. Согласно методу моментов приравниваем, например, соответствующие начальные моменты первого порядка, т. е. среднюю выборки в x и математическое ожидание распределения M[X]. Здесь достаточно одного уравнения относительно этого параметра:
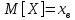
Поскольку математическое ожидание является функцией параметра
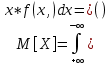
соотношение (1) можно рассматривать как уравнение с одним неизвестным, которое определяет точечную оценку параметра , являющуюся функцией.
2. Оценка двух параметров. Пусть задана функция плотности распределения
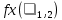 . Для нахождения неизвестных параметров нужно иметь два уравнения, поэтому приравняем друг другу соответственно начальные теоретические и эмпирические моменты первого и второго порядков:
. Для нахождения неизвестных параметров нужно иметь два уравнения, поэтому приравняем друг другу соответственно начальные теоретические и эмпирические моменты первого и второго порядков: 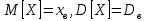
Поскольку M[X] и D [X] есть функции от
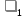 и
и 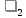 , соотношения (3)
, соотношения (3)определяют точечные оценки этих параметров как функции от выборки:
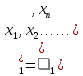
Метод наименьших квадратов: Этот метод используется для оценки параметров линейной регрессионной модели. Он заключается в минимизации суммы квадратов разностей между наблюдаемыми значениями зависимой переменной и прогнозными значениями, полученными на основе модели. Метод наименьших квадратов позволяет найти оптимальные значения параметров модели, которые наилучшим образом соответствуют данным. Этот метод широко применяется в
регрессионном анализе и имеет множество вариаций, таких как метод наименьших абсолютных значений и взвешенных наименьших квадратов.
В основу этого метода положена идея минимизации суммы квадратов отклонений фактических значений у от их выравненных (теоретических) значений
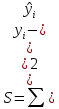
где уi – фактические значения результативного признака;
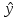 – теоретические значения результативного признака, найденные по уравнению регрессии.
– теоретические значения результативного признака, найденные по уравнению регрессии.Метод максимального правдоподобия
Этот метод основан на максимизации функции правдоподобия, которая представляет собой вероятность наблюдать имеющиеся данные при заданных значениях параметров модели. Метод максимального правдоподобия позволяет оценить параметры модели таким образом, чтобы вероятность наблюдаемых данных была максимальной. Этот метод является одним из наиболее мощных и широко используемых методов оценки параметров моделей и может быть применен для различных типов моделей, включая линейные, нелинейные, дискретные и непрерывные модели.
Пусть плотность распределения генеральной совокупности p(x, θ) в точке x зависит от параметра θ и у нас имеется выборка
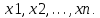
Функция правдоподобия:
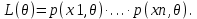
Вопрос 14
Корреляционный анализ – статистический метод, позволяющий с использованием коэффициентов корреляции определить, существует ли зависимость между переменными и насколько она сильна.
Теснота связи количественно выражается величиной коэффициентов корреляции. Построение коэффициентов корреляции основано на сумме произведений отклонений индивидуальных значений признаков xi и yi от их средних значений x и y :
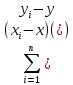
Коэффициент корреляции – двумерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных.
Для расчета линейного (парного) коэффициента корреляции можно воспользоваться также следующей формулой: