ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 45
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таблица 4 - Интервальный вариационный ряд признака X
| Карман | Частота | Интегральный % |
| 4,06 | 4 | 13,33% |
| 6,06 | 4 | 26,67% |
| 8,06 | 5 | 43,33% |
| 10,06 | 5 | 60,00% |
| 12,06 | 3 | 70,00% |
| 14,06 | 8 | 96,67% |
| 16,06 | 1 | 100,00% |
| Еще | 0 | 100,00% |
| | | |
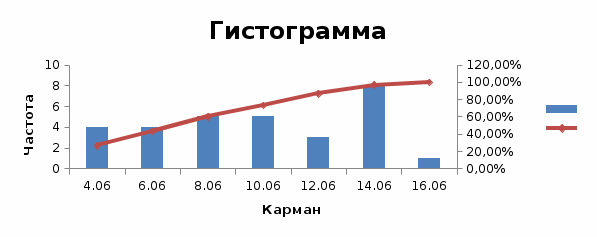
Рисунок 2 – Гистограмма и полигон распределения признака Х Оценить статистические характеристики рядов распределения.
Для дискретного вариационного ряда находим их с помощью инструмента Анализа данных Описательная статистика.
Таблица 5 – Результаты Описательной статистики
| Y | |
| Среднее | 106,86 |
| Стандартная ошибка | 1,65 |
| Медиана | 106,69 |
| Мода | #Н/Д |
| Стандартное отклонение | 9,018 |
| Дисперсия выборки | 81,33 |
| Эксцесс | -1,018 |
| Асимметричность | -0,168 |
| Интервал | 29,67 |
| Минимум | 91,02 |
| Максимум | 120,69 |
| Сумма | 3205,93 |
| Счет | 30 |
| Уровень надежности (95,0%) | 3,367 |
Показатели центра распределения: средняя, мода, медиана Среднее значение зависимого признака Yравно:
????̅ = 106,86.
Моды – нет, так как все значения зависимого признака Yвстречаются по одному разу в совокупности.
Медиана:
Me=106,69.
Половина значений зависимой переменной меньше 119,62, а другая половина больше 119,62.
Показатели вариации признака: размах вариации, дисперсия, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии, коэффициент эксцесса.
Таблица 6 – Результаты вычисления показателей вариации
| Среднее линейное отклонение | 7,259 |
| Дисперсия выборки | 78,619 |
| Среднее квадратичное отклонение | 8,867 |
| Относительное линейное отклонение | 6,793 |
| Коэффициент вариации, % | 8,297 |
| Стандартная ошибка выборочной средней | 1,619 |
| Ошибка среднего квадратичного отклонения | 1,145 |
| Ошибка коэффициента вариации | 1,071 |
Размах вариации
R=29,67.
Наибольшее значение признака Y превышает наименьшее на 67,79. Дисперсия:
????2 =
78,69.
Среднее квадратическое отклонение:
???? = 8,867.
Каждое значение признака Y в среднем отличается от среднего значения на 8,867.
Относительное линейное отклонение:
???????? =
????
 ????̅ ∗ 100% =
????̅ ∗ 100% =7,259
 ∗ 100% = 6,8 %
∗ 100% = 6,8 %106,86
Коэффициент вариации:
????
 ???????? = ????̅ ∗ 100% =
???????? = ????̅ ∗ 100% =8,867
 ∗ 100% = 8,3 %
∗ 100% = 8,3 %106,86
Так как 33%, ???????? то совокупность значений признака Yоднородная, вариация значений признака Yне сильная.
Для интервального вариационного ряда признака Хпроведем дополнительные вычисления (таблица 7).
Таблица 7 – Промежуточные вычисления
| № п/п | Интервал | Середина интервала, X i | Частота, | Xini | Накопленная частота Si | x- x ni | (x- x)2 n |
| ni | |||||||
| 1 | 2,06-4,06 | 3,06 | 4 | 12,24 | 4 | 23,200 | 134,560 |
| 2 | 4,06-6,06 | 5,06 | 4 | 20,24 | 8 | 15,200 | 57,760 |
| 3 | 6,06-8,06 | 7,06 | 5 | 35,3 | 13 | 9,000 | 16,200 |
| 4 | 8,06-10,06 | 9,06 | 5 | 45,3 | 18 | 1,000 | 0,200 |
| 5 | 10,06-12,06 | 11,06 | 3 | 33,18 | 21 | 6,600 | 14,52 |
| 6 | 12,06-14,06 | 13,06 | 8 | 104,48 | 29 | 33,600 | 141,12 |
| 7 | 14,06-16,06 | 15,06 | 1 | 15,06 | 30 | 6,200 | 38,44 |
| Итого | - | 30 | 265,8 | - | 94,800 | 402,8 | |
Среднее значение признака X:
∑????
????????????????
265,8
????̅ = ????=1 =
∑ ????????
= 8,860
 30
30Мода:
???????? = 12,89
Медиана:
????e = 8,86
Половина значений признака Хменьше 8,86, и другая половина значений признака
Хбольше 8,86.
Размах вариации:
R= 4,87
Среднее линейное отклонение:
d = 3,16
Дисперсия:
????2 = 13,427
Среднее квадратическое отклонение:
???? = 3,664
Каждое значение признака Х в среднем отличается от среднего значения на 3,45.
Относительное линейное отклонение:
???????? =
3,16
 ∗ 100% = 35,66%
∗ 100% = 35,66%8,86
Коэффициент вариации:
???????? =
3,664
 ∗ 100% = 41,36%
∗ 100% = 41,36%8,86
Так как 33%, ???????? то совокупность значений признака Хявляется однородной, вариация значений признака Хсильная.
С помощью критерия Пирсона проверим гипотезу о нормальном распределении случайной величины Х.
Таблица 8 – Промежуточные вычисления
| № | xi | xi+1 | ni | ui | ui+1 | Ф(ui) | Ф(ui+1) | pi | ni | (ni− ni')2 ni' |
| 1 | 2,06 | 4,06 | 4 | -1,86 | -1,31 | -0,500 | -0,405 | 0,095 | 2,85 | 0,46 |
| 2 | 4,06 | 6,06 | 4 | -1,31 | -0,76 | -0,405 | -0,278 | 0,127 | 3,82 | 0,0086 |
| 3 | 6,06 | 8,06 | 5 | -0,76 | -0,22 | -0,278 | -0,086 | 0,191 | 5,74 | 0,09 |
| 4 | 8,06 | 10,06 | 5 | -0,22 | 0,33 | -0,086 | 0,128 | 0,215 | 6,44 | 0,32 |
| 5 | 10,06 | 12,06 | 3 | 0,33 | 0,87 | 0,128 | 0,309 | 0,180 | 5,41 | 1,07 |
| 6 | 12,06 | 14,06 | 8 | 0,87 | 1,42 | 0,309 | 0,422 | 0,113 | 3,40 | 6,23 |
| 7 | 14,06 | 16,06 | 1 | 1,42 | 1,96 | 0,422 | 0,500 | 0,078 | 2,34 | 0,77 |
| Итого | – | – | 30 | – | – | – | – | 1,000 | 30,00 | 8,19 |
Получили наблюдаемое значение критерия Пирсона:
набл
????2 = 8,19
Табличное значение критерия Пирсона при уровне значимости = 0,05 и k=4 составляет:
кр
????2 = 9,5
Расчетное значение критерия Пирсона меньше табличного ????2 < ????2 (8,19 < 9,5),
набл кр
следовательно, случайная величина Храспределена по нормальному закону.
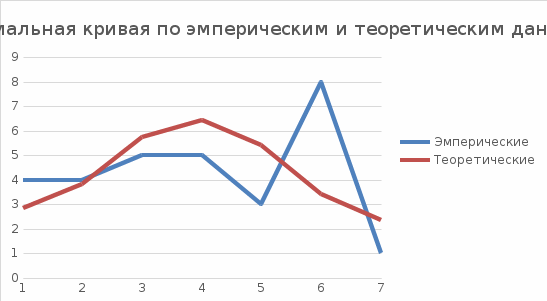
Рисунок 3 – Нормальная кривая по эмпирическим и теоретическим данным
Выполним статистическую оценку (точечную и интервальную) параметров распределения.
Стандартная ошибка выборочной средней:
???? ̅ = ????

???? √????
Ошибка среднего квадратического отклонения:
????????
= ????
 √2????
√2????Ошибка коэффициента вариации:
????
 ???????? =
???????? = √2????
Для переменной Yполучим:
???? ̅ = 8,867 = 1,62

???? √30
8,867
 ???????? = = 1,14
???????? = = 1,14√2 ∗ 30
8,297
 ???????? = = 1,07
???????? = = 1,07√2 ∗ 30
Для переменной Хпо интервальному ряду получим:
3,664
 ????????̅ = = 0,669
????????̅ = = 0,669√30
3,664
 ???????? = = 0,473
???????? = = 0,473√2 ∗ 30
41,357
 ???????? = = 5,34
???????? = = 5,34√2 ∗ 30
Оценим достоверность выборочной средней, среднего квадратического отклонения и коэффициент вариации по t-критерию Стьюдента.
Для доверительной вероятности 0,95 по интегральной таблице Лапласа
Ф(????) = 0,95 = 0,475 он равен: ????

= 1,96