ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 51
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Коэффициент корреляции Спирмена — это мера статистической связи между двумя ранговыми переменными. Он измеряет степень монотонной связи между переменными, то есть, связь, при которой значения одной переменной увеличиваются или уменьшаются вместе с изменением значений другой переменной, но не обязательно с постоянной скоростью. Коэффициент Спирмена принимает значения от -1 до 1, где -1 означает полную обратную монотонную связь, 1 - полную прямую монотонную связь, и 0 - отсутствие монотонной связи.
Коэффициент корреляции Кендалла - это также мера статистической связи между двуми ранговыми переменными, но он измеряет степень ранговой конкордации, то есть, степень согласованности между двуми переменными в отношении их порядка. Коэффициент Кендалла также принимает значения от -1 до 1, где -1 означает полную обратную конкордацию, 1 - полную прямую конкордацию, и 0 - отсутствие конкордации.
В качестве условных обозначений признаков и оценки связей между ними также используются ранги и ранговые коэффициенты связи.
Ранжирование – это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения.
Ранг – это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин.
Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест. Такие ранги называют связными. Принцип нумерации значений исследуемых признаков является основой непараметрических методов изучения взаимосвязи между социально-экономическими явлениями и процессами. Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмера (р) и Кендалла (т). эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками, при условии, если их значения упорядочить или про ранжировать по степени убывания или возрастания признака. Для случая, когда нет связных рангов коэффициент рангов Спирмена рассчитывается по формуле:
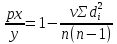
Где, (di)^2 – квадрат разности рангов;
n – число наблюдений (число пар рангов)
Ранговый коэффициент корреляции Кендала может также использоваться для измерения взаимосвязи между качественными и количественными признаками,
характеризующими однородные объекты, ранжированные по одному принципу. Ранговый коэффициент корреляции Кендала для случая, когда нет связных рангов:
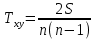
Где n – число наблюдений,
S – сумма разностей между числом последовательностей и числом инверсий по второму признаку: S = P – Q.
Расчет данного коэффициента выполняется в следующей последовательности:
1) значения х ранжируются в порядке возрастания или убывания;2) значения у располагаются в порядке, соответствующем значениям х;3) для каждого ранга y определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа, определяют величину Р как меру соответствия последовательности рангов по х и у и учитываются со знаком (+)
4) для каждого ранга у определяется число следующих за ним значений рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком минус.
Ранговые коэффициенты Спирмена, Кендалла и конкордации имеют то преимущество, что с помощью их можно измерять и оценивать связи как между количественными, так и между атрибутивными признаками, которые поддаются ранжированию.
Практическая часть 1
| № | Х | У |
| 1 | 5,07 | 99,53 |
| 2 | 3,49 | 108,84 |
| 3 | 11,05 | 106,29 |
| 4 | 3,06 | 105,34 |
| 5 | 3,47 | 96,35 |
| 6 | 5,47 | 106,74 |
| 7 | 6,06 | 116,64 |
| 8 | 13,62 | 94,78 |
| 9 | 13,70 | 118,69 |
| 10 | 14,90 | 91,52 |
| 11 | 7,87 | 115,75 |
| 12 | 6,74 | 120,69 |
| 13 | 12,32 | 110,49 |
| 14 | 8,34 | 119,68 |
| 15 | 13,86 | 104,11 |
| 16 | 10,95 | 106,64 |
| 17 | 13,54 | 91,02 |
| 18 | 9,72 | 118,54 |
| 19 | 10,71 | 119,35 |
| 20 | 4,97 | 105,93 |
| 21 | 7,14 | 106,83 |
| 22 | 13,95 | 94,13 |
| 23 | 7,00 | 111,35 |
| 24 | 13,19 | 110,00 |
| 25 | 3,44 | 105,26 |
| 26 | 9,51 | 94,42 |
| 27 | 8,83 | 101,25 |
| 28 | 12,43 | 115,20 |
| 29 | 8,61 | 112,90 |
| 30 | 6,07 | 97,67 |
Решение задачи № 1: Таблица 1 – Исходные данные
Решение:
Построить по зависимому признаку Yдискретный вариационный ряд, по независимому признаку Х– интервальный вариационный ряд. Построить полигон и гистограмму.
Таблица 2 – Дискретный вариационный ряд признака Y
| № п/п | Y | ni |
| 17,00 | 91,02 | 1 |
| 10,00 | 91,52 | 1 |
| 22,00 | 94,13 | 1 |
| 26,00 | 94,42 | 1 |
| 8,00 | 94,78 | 1 |
| 5,00 | 96,35 | 1 |
| 30,00 | 97,67 | 1 |
| 1,00 | 99,53 | 1 |
| 27,00 | 101,25 | 1 |
| 15,00 | 104,11 | 1 |
| 25,00 | 105,26 | 1 |
| 4,00 | 105,34 | 1 |
| 20,00 | 105,93 | 1 |
| 3,00 | 106,29 | 1 |
| 16,00 | 106,64 | 1 |
| 6,00 | 106,74 | 1 |
| 21,00 | 106,83 | 1 |
| 2,00 | 108,84 | 1 |
| 24,00 | 110,00 | 1 |
| 13,00 | 110,49 | 1 |
| 23,00 | 111,35 | 1 |
| 29,00 | 112,90 | 1 |
| 28,00 | 115,20 | 1 |
| 11,00 | 115,75 | 1 |
| 7,00 | 116,64 | 1 |
| 18,00 | 118,54 | 1 |
| 9,00 | 118,69 | 1 |
| 19,00 | 119,35 | 1 |
| 14,00 | 119,68 | 1 |
| 12,00 | 120,69 | 1 |
| Итого | 3205,93 | 30 |
Построим полигон (рисунок 1)
Рисунок 1 – Полигон распределения признака Y
Расположим значения независимого признака Х по возрастанию.
Таблица 3 – Значения признака Х по возрастанию
| № | Х |
| 4 | 3,06 |
| 25 | 3,44 |
| 5 | 3,47 |
| 2 | 3,49 |
| 20 | 4,97 |
| 1 | 5,07 |
| 6 | 5,47 |
| 7 | 6,06 |
| 30 | 6,07 |
| 12 | 6,74 |
| 23 | 7 |
| 21 | 7,14 |
| 11 | 7,87 |
| 14 | 8,34 |
| 29 | 8,61 |
| 27 | 8,83 |
| 26 | 9,51 |
| 18 | 9,72 |
| 19 | 10,71 |
| 16 | 10,95 |
| 3 | 11,05 |
| 13 | 12,32 |
| 28 | 12,43 |
| 24 | 13,19 |
| 17 | 13,54 |
| 8 | 13,62 |
| 9 | 13,7 |
| 15 | 13,86 |
| 22 | 13,95 |
| 10 | 14,9 |