ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 48
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2 кр
Доверительный интервал для среднего значения определяется следующим образом:
????̅ − ????кр
∗ ????
 √????
√????≤ ???? ≤ ????̅ + ????кр
∗ ????
 √????
√????????̅ − ????кр ∗ ????????̅ ≤ ???? ≤ ????̅ + ????кр ∗ ????????̅
Для переменной Yполучим:
106,86 – 1,96 * 1,62 ≤ a ≤ 106,86 + 1,96 * 1,62
103,69 ≤ a ≤ 110,04
C вероятностью 0,95 среднее значение показателя Yв генеральной совокупности будет находиться в пределах от 103,69 до 110,04.
Для переменной Х по интервальному ряду: 8,860 – 1,96 * 0,669 ≤ a ≤ 8,860 + 1,96 *0,669
7,55 ≤ a ≤ 10,17
C вероятностью 0,95 среднее значение показателя Хв генеральной совокупности будет находиться в пределах от 7,55 до 10,17.
Доверительный интервал среднего квадратического отклонения определяется следующим образом:
s(1− q) s(1+ q),
где s – исправленное среднее квадратическое отклонение;
q – находится по таблице.
Для уровня значимости 0,05 и n = 30: q = 0,28.
Для переменной Y: s = 11,600;
9,02 (1− 0,28) 9,02 (1+ 0,28).
8,49 11,55.
C вероятностью 0,95 среднее квадратическое отклонение показателя Y в генеральной совокупности будет находиться в пределах от 8,352 до 14,848.
Для переменной Х по интервальному ряду:
S = 3,73
3,73 (1− 0,28) 3,73 (1+ 0,28);
2,69 4,77
C вероятностью 0,95 среднее квадратическое отклонение показателя Х в генеральной совокупности будет находиться в пределах от 2,69 до 4,77.
Практическая часть 2
Решение задачи № 2:
Таблица 9 - Значения признака Хи Y
| Х | У |
| 5,07 | 99,53 |
| 3,49 | 108,84 |
| 11,05 | 106,29 |
| 3,06 | 105,34 |
| 3,47 | 96,35 |
| 5,47 | 106,74 |
| 6,06 | 116,64 |
| 13,62 | 94,78 |
| 13,7 | 118,69 |
| 14,9 | 91,52 |
| 7,87 | 115,75 |
| 6,74 | 120,69 |
| 12,32 | 110,49 |
| 8,34 | 119,68 |
| 13,86 | 104,11 |
| 10,95 | 106,64 |
| 13,54 | 91,02 |
| 9,72 | 118,54 |
| 10,71 | 119,35 |
| 4,97 | 105,93 |
| 7,14 | 106,83 |
| 13,95 | 94,13 |
| 7 | 111,35 |
| 13,19 | 110 |
| 3,44 | 105,26 |
| 9,51 | 94,42 |
| 8,83 | 101,25 |
| 12,43 | 115,2 |
| 8,61 | 112,9 |
| 6,07 | 97,67 |
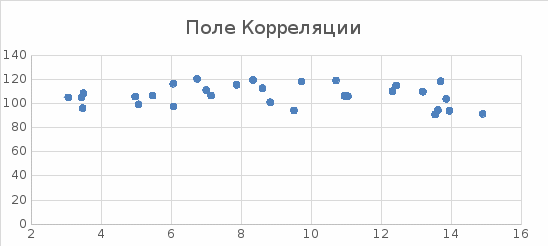
Построим поле корреляции (рисунок 4).
| Регрессионнаястатистика | ||||||
| Множественный R | 0,13 | |||||
| R-квадрат | 0,017 | |||||
| Нормированный R-квадрат | -0,018 | |||||
| Стандартная ошибка | 9,099 | |||||
| Наблюдения | 30 | |||||
| Таблица 11 - Дисперсионный анализ | ||||||
| | df | SS | MS | F | ЗначимостьF | |
| Регрессия | 1 | 40,228 | 40,23 | 0,485 | 0,4915 | |
| Остаток | 28 | 2318,36 | 15,91 | | | |
| Итого | 29 | 2358,58 | 82,79 | | | |
Рисунок 4 – Поле корреляции Таблица 10 – Регрессионная статистика
Таблица 12 - Результаты регрессионного анализа
| | Коэффи-циенты | Стандартнаяошибка | t-статисти- ка | P- Значе-ние | Ниж-ние 95% | Верх-ние 95% | Ниж-ние 95,0% | Верх-ние 95,0% |
| Y-пересече- ние | 109,7 | 4,396 | 24,95 | 1,141E-20 | 100,69 | 118,7 | 100,69 | 118,7 |
| Х | -0,316 | 0,45 | -0,697 | 0,49 | -1,25 | 0,61 | -1,25 | 0,61 |
Получили следующее уравнение линейной регрессии:
????
????^ = -0,3163x *X+ 109,7
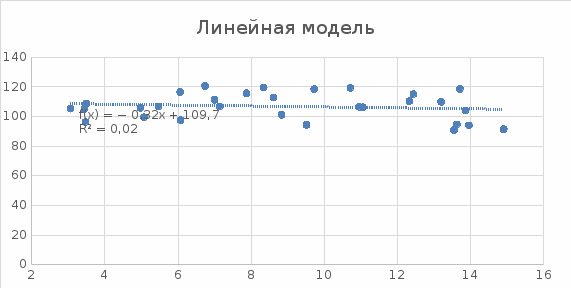
Рисунок 5 – Линейная модель
Коэффициент детерминации равен:
????2 = 0,0171
1,71 % вариации зависимого признака Yобъясняется вариацией зависимого признака X
Средний коэффициент эластичности:
Э̅ = -0,1306
При увеличении признака X значения признака Yуменьшается на 13%
Средняя ошибка аппроксимации:
 А̅ = 209,69 = 6,99 %
А̅ = 209,69 = 6,99 %30
В среднем расчётные значения отклоняются от фактических на 6,99%, что говорит о приемлемом качестве модели
Таблица 13 – Вывод отстатка
| Наблюдение | Предсказанное У | Остатки | y-y |
| 1 | 108,0978828 | -8,567882838 | 8,608342046 |
| 2 | 108,597714 | 0,242286024 | 0,222607519 |
| 3 | 106,2061169 | 0,083883115 | 0,078919103 |
| 4 | 108,733744 | -3,39374397 | 3,221704927 |
| 5 | 108,604041 | -12,25404095 | 12,71825735 |
| 6 | 107,9713433 | -1,23134331 | 1,153591259 |
| 7 | 107,7846975 | 8,855302495 | 7,591994595 |
| 8 | 105,3931004 | -10,61310041 | 11,19761597 |
| 9 | 105,3677925 | 13,32220749 | 11,22437231 |
| 10 | 104,9881739 | -13,46817392 | 14,71609913 |
| 11 | 107,2121061 | 8,537893862 | 7,376150205 |
| 12 | 107,5695803 | 13,12041969 | 10,87117383 |
| 13 | 105,8043539 | 4,685646118 | 4,240787509 |
| 14 | 107,0634222 | 12,61657781 | 10,54192664 |
| 15 | 105,3171767 | -1,207176697 | 1,159520408 |
| 16 | 106,2377518 | 0,402248233 | 0,377202019 |
| 17 | 105,4184083 | -14,39840832 | 15,81895003 |
| 18 | 106,6268608 | 11,91313918 | 10,04988964 |
| 19 | 106,3136755 | 13,03632452 | 10,92276876 |
| 20 | 108,1295177 | -2,19951772 | 2,076387917 |
| 21 | 107,4430408 | -0,613040778 | 0,573847026 |
| 22 | 105,2887053 | -11,1587053 | 11,85456847 |
| 23 | 107,4873296 | 3,862670387 | 3,468945117 |
| 24 | 105,5291304 | 4,470869593 | 4,064426903 |
| 25 | 108,6135314 | -3,353531417 | 3,185950425 |
| 26 | 106,6932941 | -12,27329407 | 12,99861689 |
| 27 | 106,9084113 | -5,658411269 | 5,58855434 |
| 28 | 105,7695555 | 9,430444489 | 8,18614973 |
| 29 | 106,978008 | 5,92199199 | 5,245342772 |
| 30 | 107,781534 | -10,11153402 | 10,35275317 |
| Итог | | | 209,687416 |
F-критерий Фишера для уравнения регрессии в целом равен:
????факт = 0,486
Критическое значение F- критерия при уровне значимости = 0,05 и степенях свободы k1 = m = 1 и k2 = n – m -1 = 30 − 1 – 1 = 28:
????крит = 4,196
Так как ????факт < ????крит, то линейное уравнение регрессии не является значимым.
t-критерий Стьюдента для параметров:
???????? = 24,95
???????? = -0,697
Критическое значение t-критерия при уровне значимости = 0,05 и k = n − 2 = 30 − 2 = 28 составляет:
????табл = 2,048
Так как ???????? ????табл, то параметр aявляется значимым, ???????? < ????табл., то параметр b
значимый
Берем модель y=109,95+1,1x вместо x подставляем Xмакс.
0,8*14,9=11,92
Yпрогноз=109,95+1,1*11,92
Yпрогноз=105,93
ЗАКЛЮЧЕНИЕ
В ходе выполнения расчетно-графической работы было сделано: теоретическая часть, и практическая часть, состоящая из 2 задач.
В теоретической части рассмотрели следующие вопросы: Метод моментов. Метод наименьших квадратов. Метод максимального правдоподобия. Корреляционный анализ качественных показателей. Ранговые коэффициенты корреляции Спирмена и Кендалла. Это было сделано с целью углубить знания студентов по отдельным разделам научной методологии и методики анализа данных в соответствии с тематической направленностью теоретической части работы.
В ходе решение практической части были получены навыки расчета теоретических данных с помощью программы Excel.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
-
[Электронный ресурс]. – Режим доступа: https://studfile.net/preview/7410005/page:6/ (Дата обращения 01.05.2023) -
[Электронный ресурс]. – Режим доступа: https://studfile.net/preview/9066694/ (Дата обращения 01.05.2023) -
[Электронный ресурс]. – Режим доступа: https://polyakov.imamod.ru/arc/stud/popov/lecture_21.pdf Дата обращения 01.05.2023) -
[Электронный ресурс]. – Режим доступа: https://mse.msu.ru/wp-content/uploads/2020/03/Лекция-3-методы-оценивания.pdf (Дата обращения 01.05.2023)