Файл: Протокол 1 от 14 сентября 2015г. Согласовано зам директора по увр Волкова О. Н.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 139
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тематическое планирование
с определением основных видов учебной деятельности и метапредметных умений и навыков
МАТЕМАТИКА
5-6 классы (350 ч)
Тематическое планирование
7-9 классы. Раздел «Алгебра» (315ч)
Раздел « Геометрия» 7-9 классы (210 ч)
VII. Описание учебно-методического и материально-технического обеспечения образовательного процесса
Оснащение процесса обучения математике обеспечивается библиотечным фондом, печатными пособиями, а также информационно-коммуникативными средствами, экранно-звуковыми пособиями, техническими средствами обучения, учебно-практическим и учебно-лабораторным оборудованием.
В библиотечный фонд входят Стандарт по математике, примерные программы, авторские программы, комплекты учебников, рекомендованных или допущенных Министерством образования и науки Российской Федерации. В состав библиотечного фонда входят рабочие тетради, дидактические материалы, сборники контрольных и самостоятельных работ, практикумы по решению задач, соответствующие используемым комплектам учебников; сборники заданий, обеспечивающих диагностику и контроль качества обучения в соответствии с требованиями к уровню подготовки выпускников, закрепленными в Стандарте по математике; учебная литература, необходимую для подготовки докладов, сообщений, рефератов, творческих работ.
В комплект печатных пособий включены таблицы по математике, в которых представлены правила действий с числами, таблицы метрических мер, основные сведения о плоских и пространственных геометрических фигурах, основные математические формулы, соотношения, законы, графики функций.
Информационные средства обучения - мультимедийные обучающие программы и электронные учебные издания, ориентированные на систему дистанционного обучения либо имеющие проблемно-тематический характер и обеспечивающие дополнительные условия для изучения отдельных тем и разделов Стандарта. Эти пособия предоставляют техническую возможность построения системы текущего и итогового контроля уровня подготовки учащихся (в том числе в форме тестового контроля). Инструментальная среда предоставляет возможность построения и исследования геометрических чертежей, графиков функций, проведения числовых и вероятностно-статистических экспериментов.
Минимальный набор учебного оборудования включает:
Библиотечный фонд
с определением основных видов учебной деятельности и метапредметных умений и навыков
МАТЕМАТИКА
5-6 классы (350 ч)
| Основное содержание по темам | Характеристика основных видов деятельности ученика (на уровне учебных действий) | Метапредметные умения и навыки |
| 1 | 2 | 3 |
| ||
| Натуральный ряд. Десятичная система счисления. Арифметические действия с натуральными числами. Свойства арифметических действий. Понятие о степени с натуральным показателем. Квадрат и куб числа. Числовые выражения, значение числового выражения. Порядок действий в числовых выражениях, использование скобок. Решение текстовых задач арифметическими способами. Делители и кратные. Наибольший общий делитель; наименьшее общее кратное. Свойства делимости. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на простые множители. Деление с остатком | Описывать свойства натурального ряда. Читать и записывать натуральные числа, сравнивать и упорядочивать их. Выполнять вычисления с натуральными числами; вычислять значения степеней. Формулировать свойства арифметических действий, записывать их с помощью букв, преобразовывать на их основе числовые выражения. Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, моделировать условие с помощью схем, рисунков, реальных предметов; строить логическую цепочку рассуждений; критически оценивать полученный ответ, осуществлять самоконтроль, проверяя ответ на соответствие условию. Формулировать определения делителя и кратного, простого числа и составного числа, свойства и признаки делимости. Доказывать и опровергать с помощью контрпримеров утверждения о делимости чисел. Классифицировать натуральные числа (четные и нечетные, по остаткам от деления на 3 и т. п.). Исследовать простейшие числовые закономерности, проводить числовые эксперименты (в том числе с использованием калькулятора, компьютера) | Уметь видеть математическую задачу в контексте проблемной ситуации в окружающей жизни. Понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. |
| ||
| Обыкновенные дроби. Основное свойство дроби. Сравнение обыкновенных дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части. Десятичные дроби. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной. Отношение. Пропорция; основное свойство пропорции. Проценты; нахождение процентов от величины и величины по ее процентам; выражение отношения в процентах. Решение текстовых задач арифметическим способом | Моделировать в графической, предметной форме понятия и свойства, связанные с понятием обыкновенной дроби. Формулировать, записывать с помощью букв основное свойство обыкновенной дроби, правила действий с обыкновенными дробями. Преобразовывать обыкновенные дроби, сравнивать и упорядочивать их. Выполнять вычисления с обыкновенными дробями. Читать и записывать десятичные дроби. Представлять обыкновенные дроби в виде десятичных и десятичные в виде обыкновенных; находить десятичные приближения обыкновенных дробей. Сравнивать и упорядочивать десятичные дроби. Выполнять вычисления с десятичными дробями. Использовать эквивалентные представления дробных чисел при их сравнении, при вычислениях. Выполнять прикидку и оценку в ходе вычислений. Объяснять, что такое процент. Представлять проценты в виде дробей и дроби в виде процентов. Осуществлять поиск информации (в СМИ), содержащей данные, выраженные в процентах, интерпретировать их. Приводить примеры использования отношений на практике. Решать задачи на проценты и дроби (в том числе задачи из реальной практики), используя при необходимости калькулятор; использовать понятия отношения и пропорции при решении задач. Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, моделировать условие с помощью схем, рисунков, реальных предметов; строить логическую цепочку рассуждений; критически оценивать полученный ответ, осуществлять самоконтроль, проверяя ответ на соответствие условию. Проводить несложные исследования, связанные со свойствами дробных чисел, опираясь на числовые эксперименты (в том числе с использованием калькулятора, компьютера) | Понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем; |
| ||
| Положительные и отрицательные числа, модуль числа. Изображение чисел точками координатной прямой; геометрическая интерпретация модуля числа. Множество целых чисел. Множество рациональных чисел. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий | Приводить примеры использования в окружающем мире положительных и отрицательных чисел (температура, выигрыш — проигрыш, выше — ниже уровня моря и т. п.). Изображать точками координатной прямой положительные и отрицательные рациональные числа. Характеризовать множество целых чисел, множество рациональных чисел. Формулировать и записывать с помощью букв свойства действий с рациональными числами, применять для преобразования числовых выражений. Сравнивать и упорядочивать рациональные числа, выполнять вычисления с рациональными числами | Понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. Умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации; |
| 4. Измерения, приближения, оценки. Зависимости между величинами (20 ч) | ||
| Примеры зависимостей между величинами: скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость и др. Представление зависимостей в виде формул. Вычисления по формулам. Решение текстовых задач арифметическими способами | Выражать одни единицы измерения величины в других единицах (метры в километрах, минуты в часах и т. п.). Округлять натуральные числа и десятичные дроби. Выполнять прикидку и оценку в ходе вычислений. Моделировать несложные зависимости с помощью формул; выполнять вычисления по формулам. Использовать знания о зависимостях между величинами (скорость, время, расстояние; работа, производительность, время и т. п.) при решении текстовых задач | Уметь видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни |
| 5. Элементы алгебры (25ч) | ||
| Использование букв для обозначения чисел, для записи свойств арифметических действий. Буквенные выражения. Числовое значение буквенного выражения. Уравнение, корень уравнения. Нахождение неизвестных компонентов арифметических действий. Декартовы координаты на плоскости. Построение точки по ее координатам, определение координат точки на плоскости | Читать и записывать буквенные выражения, составлять буквенные выражения по условиям задач. Вычислять числовое значение буквенного выражения при заданных значениях букв. Составлять уравнения по условиям задач. Решать простейшие уравнения на основе зависимостей между компонентами арифметических действий. Строить на координатной плоскости точки и фигуры по заданным координатам; определять координаты точек | Уметь видеть математическую задачу в контексте проблемной ситуации в окружающей жизни. Понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. Первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов; |
| 6. Описательная статистика. Вероятность. Комбинаторика. Множества (20ч) | ||
| Представление данных в виде таблиц, диаграмм. Понятие о случайном опыте и событии. Достоверное и невозможное события. Сравнение шансов. Решение комбинаторных задач перебором вариантов | Извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным, сравнивать величины, находить наибольшие и наименьшие значения и др. Выполнять сбор информации в несложных случаях, представлять информацию в виде таблиц и диаграмм, в том числе с помощью компьютерных программ. Приводить примеры случайных событий, достоверных и невозможных событий. Сравнивать шансы наступления событий; строить речевые конструкции с использованием словосочетаний более вероятно, маловероятно и др. Выполнять перебор всех возможных вариантов для пересчета объектов или комбинаций, выделять комбинации, отвечающие заданным условиям Приводить примеры конечных и бесконечных множеств. Находить объединение и пересечение конкретных множеств. Приводить примеры несложных классификаций из различных областей жизни. Иллюстрировать теоретико-множественные понятия с помощью кругов Эйлера | Уметь видеть математическую задачу в контексте проблемной ситуации в окружающей жизни. Умение выдвигать гипотезы при решении учебных задач, понимать необходимость их пров ерки |
| 7. Наглядная геометрия (45 ч) | ||
| Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, правильный многоугольник, окружность, круг. Четырехугольник, прямоугольник, квадрат. Треугольник, виды треугольников. Изображение геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности. Длина отрезка, ломаной. Периметр многоугольника. Единицы измерения длины. Измерение длины отрезка, построение отрезка заданной длины. Угол. Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника и площадь квадрата. Равновеликие фигуры. Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники, правильные многогранники. Примеры разверток многогранников, цилиндра и конуса. Понятие объема; единицы объема. Объем прямоугольного параллелепипеда и объем куба. Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур | Распознавать на чертежах, рисунках и моделях геометрические фигуры, конфигурации фигур (плоские и пространственные). Приводить примеры аналогов геометрических фигур в окружающем мире. Изображать геометрические фигуры и их конфигурации от руки и с использованием чертежных инструментов. Изображать геометрические фигуры на клетчатой бумаге. Измерять с помощью инструментов и сравнивать длины отрезков и величины углов. Строить отрезки заданной длины с помощью линейки и циркуля и углы заданной величины с помощью транспортира. Выражать одни единицы измерения длин через другие. Вычислять площади квадратов и прямоугольников, используя формулы площади квадрата и площади прямоугольника. Выражать одни единицы измерения площади через другие. Изготавливать пространственные фигуры из разверток; распознавать развертки куба, параллелепипеда, пирамиды, цилиндра и конуса.Рассматриватьпростейшие сечения пространственных фигур, получаемые путем предметного или компьютерного моделирования, определять их вид. Вычислять объемы куба и прямоугольного параллелепипеда, используя формулы объема куба и объема прямоугольного параллелепипеда. Выражать одни единицы измерения объема через другие. Исследовать и описывать свойства геометрических фигур (плоских и пространственных), используя эксперимент, наблюдение, измерение. Моделировать геометрические объекты, используя бумагу, пластилин, проволоку и др. Использовать компьютерное моделирование и эксперимент для изучения свойств геометрических объектов. Находить в окружающем мире плоские и пространственные симметричные фигуры. Решать задачи на нахождение длин отрезков, периметров многоугольников, градусной меры углов, площадей квадратов и прямоугольников, объемов кубов и прямоугольных параллелепипедов, куба. Выделять в условии задачи данные, необходимые для ее решения, строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи. Изображать равные фигуры, симметричные фигуры | Строить логическую цепочку рассуждений, сопоставлять полученный результат с условием задачи. Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера; |
| Резерв времени - 30 ч | ||
Тематическое планирование
7-9 классы. Раздел «Алгебра» (315ч)
| Основное содержание по темам | Характеристика основных видов деятельности ученика (на уровне учебных действий) | Метапредметные умения и навыки |
| 1 | 2 | 3 |
| ||
| Расширение множества натуральных чисел до множества целых, множества целых чисел до множества рациональных. Рациональное число как отношение т/п, где т — целое число, а п — натуральное число. Степень с целым показателем. Квадратный корень из числа. Корень третьей степени. Понятие об иррациональном числе. Иррациональность числа 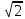 и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел. и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел.Множество действительных чисел; представление действительных чисел в виде бесконечных десятичных дробей. Сравнение действительных чисел. Взаимно однозначное соответствие между действительными числами и точками координатной прямой. Числовые промежутки: интервал, отрезок, луч | Описывать множество целых чисел, множество рациональных чисел, соотношение между этими множествами. Сравнивать и упорядочивать рациональные числа, выполнять вычисления с рациональными числами, вычислять значения степеней с целым показателем. Формулировать определение квадратного корня из числа. Использовать график функции у = х2 для нахождения квадратных корней. Вычислять точные и приближенные значения корней, используя при необходимости калькулятор; проводить оценку квадратных корней. Формулировать определение корня третьей степени; находить значения кубических корней, при необходимости используя, калькулятор. Приводить примеры иррациональных чисел; распознавать рациональные и иррациональные числа; изображать числа точками координатной прямой. Находить десятичные приближения рациональных и иррациональных чисел; сравнивать и упорядочивать действительные числа. Описывать множество действительных чисел. Использовать в письменной математической речи обозначения и графические изображения числовых множеств, теоретико-множественную символику | Умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации. Умение находить в различных источниках информацию, необходимую для решения математических проблем, представлять ее в понятной форме, принимать решение в условиях неполной и избыточной, точной и вероятностной информации. |
| ||
| Приближенное значение величины, точность приближения. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире.. Прикидка и оценка результатов вычислений. Способы записи значений величин, в том числе с выделением множителя — степени 10 в записи числа | Находить, анализировать, сопоставлять числовые характеристики объектов окружающего мира. Использовать запись чисел в стандартном виде для выражения размеров объектов, длительности процессов в окружающем мире. Сравнивать числа и величины, записанные с использованием степени 10. Использовать разные формы записи приближенных значений; делать выводы о точности приближения по записи приближенного значения. Выполнять вычисления с реальными данными. Выполнять прикидку и оценку результатов вычислений | Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Выполнять вычисления с реальными данными. |
| ||
| Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество | Выполнять элементарные знаково-символические действия: применять буквы для обозначения чисел, для записи общих утверждений; составлять буквенные выражения по условиям, заданным словесно, рисунком или чертежом; преобразовывать алгебраические суммы и произведения (выполнять приведение подобных слагаемых, раскрытие скобок, упрощение произведений). Вычислять числовое значение буквенного выражения; находить область допустимых значений переменных в выражении | Понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. Понимать и использовать математические средства наглядности (диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации. |
| ||
| Степень с натуральным показателем и ее свойства. Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности. Формула разности квадратов. Преобразование целого выражения в многочлен. Разложение многочлена на множители: вынесение общего множителя за скобки, группировка, применение формул сокращенного умножения. Многочлены с одной переменной. Корень многочлена. Квадратный трехчлен, разложение квадратного трехчлена на множители | Формулировать, записывать в символической форме и обосновывать свойства степени с натуральным показателем; применять свойства степени для преобразования выражений и вычислений. Выполнять действия с многочленами. Выводить формулы сокращенного умножения, применять их в преобразованиях выражений и вычислениях. Выполнять разложение многочленов на множители. Распознавать квадратный трехчлен, выяснять возможность разложения на множители, представлять квадратный трехчлен в виде произведения линейных множителей. Применять различные формы самоконтроля при выполнении преобразований | Умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки. Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. |
| ||
| Алгебраическая дробь. Основное свойство алгебраической дроби. Сокращение дробей. Сложение, вычитание, умножение, деление алгебраических дробей. Степень с целым показателем и ее свойства. Рациональные выражения и их преобразования. Доказательство тождеств | Формулировать основное свойство алгебраической дроби и применять его для преобразования дробей. Выполнять действия с алгебраическими дробями. Представлять целое выражение в виде многочлена, дробное — в виде отношения многочленов; доказывать тождества. Формулировать определение степени с целым показателем. Формулировать, записывать в символической форме и иллюстрировать примерами свойства степени с целым показателем; применять свойства степени для преобразования выражений и вычислений | Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом; |
| ||
| Понятия квадратного корня, арифметического квадратного корня. Уравнение вида х2=а. Свойства арифметических квадратных корней: корень из произведения, частного, степени. Тождества, 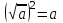 , где , где 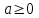 , , 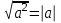 . Применение свойств арифметических квадратных корней для преобразования числовых выражений и к вычислениям. . Применение свойств арифметических квадратных корней для преобразования числовых выражений и к вычислениям. | Доказывать свойства арифметических квадратных корней; применять их для преобразования выражений. Вычислять значения выражений, содержащих квадратные корни; выражать переменные из геометрических и физических формул. Исследовать уравнение вида х2 = а; находить точные и приближенные корни при а > 0 | Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характер. |
| ||
| Уравнение с одной переменной. Корень уравнения. Свойства числовых равенств. Равносильность уравнений. Линейное уравнение. Решение уравнений, сводящихся к линейным. Квадратное уравнение. Неполные квадратные уравнения. Формула корней квадратного уравнения. Теорема Виета. Решение уравнений, сводящихся к квадратным. Биквадратное уравнение. Примеры решения уравнений третьей и четвертой степени разложением на множители. Решение дробно-рациональных уравнений. Решение текстовых задач алгебраическим способом | Распознавать линейные и квадратные уравнения, целые и дробные уравнения. Решать линейные, квадратные уравнения, а также уравнения, сводящиеся к ним; решать дробно-рациональные уравнения. Исследовать квадратные уравнения по дискриминанту и коэффициентам. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления уравнения; решать составленное уравнение; интерпретировать результат | Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов. Видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. |
| ||
| Уравнение с двумя переменными. Линейное уравнение с двумя переменными. Примеры решения уравнений в целых числах. Система уравнений с двумя переменными. Равносильность систем уравнений. Система двух линейных уравнений с двумя переменными; решение подстановкой и сложением. Решение систем двух уравнений, одно из которых линейное, а другое второй степени. Примеры решения систем нелинейных уравнений. Решение текстовых задач алгебраическим способом. Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. График линейного уравнения с двумя переменными, угловой коэффициент прямой; условие параллельности прямых. Графики простейших нелинейных уравнений (парабола, гипербола, окружность). Графическая интерпретация системы уравнений с двумя переменными | Определять, является ли пара чисел решением данного уравнения с двумя переменными; приводить примеры решения уравнений с двумя переменными. Решать задачи, алгебраической моделью которых является уравнение с двумя переменными; находить целые решения путем перебора. Решать системы двух уравнений с двумя переменными, указанные в содержании. Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления системы уравнений; решать составленную систему уравнений; интерпретировать результат. Строить графики уравнений с двумя переменными. Конструировать эквивалентные речевые высказывания с использованием алгебраического и геометрического языков. Решать и исследовать уравнения и системы уравнений на основе функционально-графических представлений уравнений | Использовать функционально-графические представления для решения и исследования уравнений и систем. Понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. Использовать математические средства наглядности графики для интерпретации, аргументации. |
| ||
| Числовые неравенства и их свойства. Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Квадратные неравенства. Системы линейных неравенств с одной переменной | Формулировать свойства числовых неравенств, иллюстрировать их на координатной прямой, доказывать алгебраически; применять свойства неравенств при решении задач. Распознавать линейные и квадратные неравенства. Решать линейные неравенства, системы линейных неравенств. Решать квадратные неравенства на основе графических представлений | Понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. Использовать математические средства наглядности графики для интерпретации, аргументации. |
| ||
| Зависимость между величинами. Представление зависимостей между величинами в виде формул. Вычисления по формулам. Прямая пропорциональная зависимость: задание формулой, коэффициент пропорциональности; свойства. Примеры прямо пропорциональных зависимостей. Обратная пропорциональная зависимость: задание формулой, коэффициент обратной пропорциональности; свойства. Примеры обратных пропорциональных зависимостей. Решение задач на прямую пропорциональность и обратную пропорциональную зависимости | Составлять формулы, выражающие зависимости между величинами, вычислять по формулам. Распознавать прямую и обратную пропорциональные зависимости. Решать текстовые задачи на прямую и обратную пропорциональные зависимости (в том числе с контекстом из смежных дисциплин, из реальной жизни) | Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки. Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач; |
| ||
| Понятие функции. Область определения и множество значений функции. Способы задания функции. График функции. Свойства функции, их отображение на графике: возрастание и убывание функции, нули функции, сохранение знака. Чтение и построение графиков функций. Примеры графиков зависимостей, отражающих реальные процессы. Функции, описывающие прямую и обратную пропорциональные зависимости, их графики. Линейная функция, ее график и свойства. Квадратичная функция, ее график и свойства. Степенные функции с натуральными показателями 2и3, их графики и свойства. Графики функций 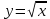 ; ; 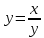 ; ; 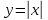 | Вычислять значения функций, заданных формулами (при необходимости использовать калькулятор); составлять таблицы значений функций. Строить по точкам графики функций. Описывать свойства функции на основе ее графического представления. Моделировать реальные зависимости формулами и графиками. Читать графики реальных зависимостей. Использовать функциональную символику для записи разнообразных фактов, связанных с рассматриваемыми функциями, обогащая опыт выполнения знаково-символических действий. Строить речевые конструкции с использованием функциональной терминологии. Использовать компьютерные программы для построения графиков функций, для исследования положения на координатной плоскости графиков функций в зависимости от значений коэффициентов, входящих в формулу. Распознавать виды изучаемых функций. Показывать схематически положение на координатной плоскости графиков изучаемых функций в зависимости от значений коэффициентов, входящих в формулы. Строить графики изучаемых функций; описывать их свойства | Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Планировать и осуществлять деятельность, направленную на решение задач исследовательского характера. |
| ||
| Понятие числовой последовательности. Задание последовательности рекуррентной формулой и формулой n-го члена. Арифметическая и геометрическая прогрессии. Формулы n-го члена арифметической и геометрической прогрессий, суммы первых п членов. Изображение членов арифметической и геометрической прогрессий точками координатной плоскости. Линейный и экспоненциальный рост. Сложные проценты | Применять индексные обозначения, строить речевые высказывания с использованием терминологии, связанной с понятием последовательности. Вычислять члены последовательностей, заданных формулой п-го члена или рекуррентной формулой. Устанавливать закономерность в построении последовательности, если известны первые несколько ее членов. Изображать члены последовательности точками на координатной плоскости. Распознавать арифметическую и геометрическую прогрессии при разных способах задания. Выводить на основе доказательных рассуждений формулы общего члена арифметической и геометрической прогрессий, суммы первых л членов арифметической и геометрической прогрессий; решать задачи с использованием этих формул. Рассматривать примеры из реальной жизни, иллюстрирующие изменение в арифметической прогрессии, в геометрической прогрессии; изображать соответствующие зависимости графически. Решать задачи на сложные проценты, в том числе задачи из реальной практики (с использованием калькулятора) | Понимать сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом. Видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. |
| ||
| Представление данных в виде таблиц, диаграмм, графиков. Случайная изменчивость. Статистические характеристики набора данных: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах. Представление о выборочном исследовании | Извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным. Определять по диаграммам наибольшие и наименьшие данные, сравнивать величины. Представлять информацию в виде таблиц, столбчатых и круговых диаграмм, в том числе с помощью компьютерных программ. Приводить примеры числовых данных (цена, рост, время на дорогу и т. д.),находить среднее арифметическое, размах числовых наборов. Приводить содержательные примеры использования средних для описания данных (уровень воды в водоеме, спортивные показатели, определение границ климатических зон) | Понимать и использовать математические средства наглядности (диаграммы, таблицы, схемы) для иллюстрации, интерпретации, аргументации. Видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. |
| ||
| Понятие о случайном опыте и случайном событии. Частота случайного события. Статистический подход к понятию вероятности. Вероятности противоположных событий. Достоверные и невозможные события. Равновозможность событий. Классическое определение вероятности Проводить случайные эксперименты, в том числе с помощью компьютерного моделирования, интерпретировать их результаты. Вычислять частоту случайного события; оценивать вероятность с помощью частоты, полученной опытным путем. Решать задачи на нахождение вероятностей событий. | Проводить случайные эксперименты, в том числе с помощью компьютерного моделирования, интерпретировать их результаты. Вычислять частоту случайного события; оценивать вероятность с помощью частоты, полученной опытным путем. Решать задачи на нахождение вероятностей событий. | Видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки. |
| ||
| Решение комбинаторных задач перебором вариантов. Комбинаторное правило умножения. Перестановки и факториал. | Выполнять перебор всех возможных вариантов для пересчета объектов или комбинаций. Применять правило комбинаторного умножения для решения задач на нахождение числа объектов или комбинаций (диагонали многоугольника, рукопожатия, число кодов, шифров, паролей и т. п.). Распознавать задачи на определение числа перестановок и выполнять соответствующие вычисления. Решать задачи на вычисление вероятности с применением комбинаторики | Понимать и использовать математические средства наглядности схемы для иллюстрации, интерпретации |
| ||
| Множество, элемент множества. Задание множеств перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество. Объединение и пересечение множеств, разность множеств. Иллюстрация отношений между множествами с помощью диаграмм Эйлера — Венна. Понятия о равносильности, следовании, употребление логических связок если то, в том и только том случае. Логические связкии, или | Приводить примеры конечных и бесконечных множеств. Находить объединение и пересечение множеств. Приводить примеры несложных классификаций. Использовать теоретико-множественную символику и язык при решении задач в ходе изучения различных разделов курса. Иллюстрировать математические понятия и утверждения примерами. Использовать примеры и контрпримеры в аргументации. Конструировать математические предложения с помощью связок если то, в том и только том случае, логических связок и, или | Понимать и использовать математические средства наглядности (диаграммы, таблицы, схемы) для иллюстрации, интерпретации, аргументации. |
| Резерв -8ч | ||
Раздел « Геометрия» 7-9 классы (210 ч)
| ||||
| Точка, прямая, плоскость. Отрезок, луч. Угол. Прямой угол, острый и тупой углы, развернутый угол. Вертикальные и смежные углы. Биссектриса угла и ее свойство. Свойства углов с параллельными и перпендикулярными сторонами. Взаимное расположение прямых на плоскости: параллельные и пересекающиеся прямые. Перпендикулярные прямые. Теоремы о параллельности и перпендикулярности прямых. Перпендикуляр и наклонная к прямой. Серединный перпендикуляр к отрезку. Геометрическое место точек. Метод геометрических мест точек. Свойства биссектрисы угла и серединного перпендикуляра к отрезку. | Формулировать и доказывать теоремы, выражающие свойства вертикальных и смежных углов, свойства и признаки параллельных прямых, о единственности перпендикуляра к прямой, свойстве перпендикуляра и наклонной, свойствах биссектрисы угла и серединного перпендикуляра к отрезку. Решать задачи на построение, доказательство и вычисления. Выделять в условии задачи условие и заключение. Опираясь на условие задачи, проводить необходимые доказательные рассуждения. Сопоставлять полученный результат с условием задачи. | Уметь находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме, понимать и использовать математические средства наглядности (чертежи) для иллюстрации, интерпретации. | ||
| 2.Треугольники (65 ч) | ||||
| Треугольники. Прямоугольные, остроугольные и тупоугольные треугольники. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников. Неравенство треугольника. Соотношения между сторонами и углами треугольника. Сумма углов треугольника. Внешние углы треугольника, теорема о внешнем угле треугольника. Теорема Фалеса. Подобие треугольников; коэффициент подобия. Признаки подобия треугольников. Теорема Пифагора. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0 до 180°; приведение к острому углу. Решение прямоугольных треугольников. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Решение треугольников: теорема косинусов и теорема синусов. Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан, высот и их продолжений | Формулировать определения прямоугольного, остроугольного, тупоугольного, равнобедренного, равностороннего треугольников; высоты, медианы, биссектрисы, средней линии треугольника; распознавать и изображать их на чертежах и рисунках. Формулировать определение равных треугольников. Формулировать и доказывать теоремы о признаках равенства треугольников. Объяснять и иллюстрировать неравенство треугольника. Формулировать и доказывать теоремы о свойствах и признаках равнобедренного треугольника, соотношениях между сторонами и углами треугольника, сумме углов треугольника, внешнем угле треугольника, о средней линии треугольника. Формулировать определение подобных треугольников. Формулировать и доказывать теоремы о признаках подобия треугольников, теорему Фалеса. Формулировать определения и иллюстрировать понятия синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника. Выводить формулы, выражающие функции угла прямоугольного треугольника через его стороны. Формулировать и доказывать теорему Пифагора. Формулировать определения синуса, косинуса, тангенса, котангенса углов от 0 до 180°. Выводить формулы, выражающие функции углов от 0 до 180° через функции острых углов. Формулировать и разъяснять основное тригонометрическое тождество. По значениям одной тригонометрической функции угла вычислять значения других тригонометрических функций этого угла. Формулировать и доказывать теоремы синусов и косинусов. Формулировать и доказывать теоремы о точках пересечения серединных перпендикуляров, биссектрис, медиан, высот или их продолжений. Исследовать свойства треугольника с помощью компьютерных программ. Решать задачи на построение, доказательство и вычисления. Выделять в условии задачи условие и заключение. Моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения. Опираясь на данные условия задачи, проводить необходимые рассуждения. Интерпретировать полученный результат и сопоставлять его с условием задачи | Умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки. Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера. | ||
| 3. Четырёхугольники (20ч) | ||||
| Четырехугольник. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная трапеция | Формулировать определения параллелограмма, прямоугольника, квадрата, ромба, трапеции, равнобедренной и прямоугольной трапеции, средней линии трапеции; распознавать и изображать их на чертежах и рисунках. Формулировать и доказывать теоремы о свойствах и признаках параллелограмма, прямоугольника, квадрата, ромба, трапеции. Исследовать свойства четырехугольников с помощью компьютерных программ. Решать задачи на построение, доказательство и вычисления. Моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения. Выделять на чертеже конфигурации, необходимые для проведения обоснований логических шагов решения. Интерпретировать полученный результат и сопоставлять его с условием задачи | Умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки. Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера. | ||
| 4. Многоугольники (10ч) | ||||
| Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Правильные многоугольники | Распознавать многоугольники, формулировать определение и приводить примеры многоугольников. Формулировать и доказывать теорему о сумме углов выпуклого многоугольника. Исследовать свойства многоугольников с помощью компьютерных программ. Решать задачи на доказательство и вычисления. Моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения. Интерпретировать полученный результат и сопоставлять его с условием задачи | Умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки. Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера. | ||
| 5. Окружность и круг (15 ч) | ||||
| Окружность и круг. Центр, радиус, диаметр. Дуга, хорда. Сектор, сегмент. Центральный, вписанный угол, величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, их свойства. Вписанные и описанные многоугольники. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные окружности правильного многоугольника. Формулы для вычисления стороны правильного многоугольника; радиуса окружности, вписанной в правильный многоугольник, радиуса окружности, описанной около правильного многоугольника | Формулировать определения понятий, связанных с окружностью, центрального и вписанного углов, секущей и касательной к окружности, углов, связанных с окружностью. Формулировать и доказывать теоремы о вписанных углах, углах, связанных с окружностью. Изображать, распознавать и описывать взаимное расположение прямой и окружности. Изображать и формулировать определения вписанных и описанных многоугольников и треугольников; окружности, вписанной в треугольник, и окружности, описанной около треугольника. Формулировать и доказывать теоремы о вписанной и описанной окружностях треугольника и многоугольника. Исследовать свойства конфигураций, связанных с окружностью, с помощью компьютерных программ. Решать задачи на построение, доказательство и вычисления. Моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения. Выделять на чертеже конфигурации, необходимые для проведения обоснований логических шагов решения. Интерпретировать полученный результат и сопоставлять его с условием задачи | Умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки. Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера. | ||
| 6 Геометрические преобразования (10ч) | ||||
| Понятие о равенстве фигур. Понятие движения: осевая и центральная симметрии, параллельный перенос, поворот. Понятие о подобии фигур и гомотетии | Объяснять и иллюстрировать понятия равенства фигур, подобия. Строить равные и симметричные фигуры, выполнять параллельный перенос и поворот. Исследовать свойства движений с помощью компьютерных программ. Выполнять проекты по темам геометрических преобразований на плоскости | Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера. | ||
| ||||
| Построения с помощью циркуля и линейки. Основные задачи на построение: деление отрезка пополам; построение угла, равного данному; построение треугольника по трем сторонам; построение перпендикуляра к прямой; построение биссектрисы угла; деление отрезка на п равных частей. | Решать задачи на построение с помощью циркуля и линейки. Находить условия существования решения, выполнять построение точек, необходимых для построения искомой фигуры. Доказывать, что построенная фигура удовлетворяет условиям задачи (определять число решений задачи при каждом возможном выборе данных) | Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Иметь первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов. | ||
| ||||
| Длина отрезка. Длина ломаной. Периметр многоугольника. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Длина окружности, число л; длина дуги окружности. Градусная мера угла, соответствие между величиной центрального угла и длиной дуги окружности. Понятие площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площади параллелограмма, треугольника и трапеции (основные формулы). Формулы, выражающие площадь треугольника через две стороны и угол между ними, через периметр и радиус вписанной окружности; формула Герона. Площадь многоугольника. Площадь круга и площадь сектора. Соотношение между площадями подобных фигур | Объяснять и иллюстрировать понятие периметра многоугольника. Формулировать определения расстояния между точками, от точки до прямой, между параллельными прямыми. Формулировать и объяснять свойства длины, градусной меры угла, площади. Формулировать соответствие между величиной центрального угла и длиной дуги окружности. Объяснять и иллюстрировать понятия равновеликих и равносоставленных фигур. Выводить формулы площадей прямоугольника, параллелограмма, треугольника и трапеции, а также формулу, выражающую площадь треугольника через две стороны и угол между ними, длину окружности, площадь круга. Находить площадь многоугольника разбиением на треугольники и четырехугольники. Объяснять и иллюстрировать отношение площадей подобных фигур. Решать задачи на вычисление линейных величин, градусной меры угла и площадей треугольников, четырехугольников и многоугольников, длины окружности и площади круга. Опираясь на данные условия задачи, находить возможности применения необходимых формул, преобразовывать формулы. Использовать формулы для обоснования доказательных рассуждений в ходе решения. Интерпретировать полученный результат и сопоставлять его с условием задачи | Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Иметь первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов | ||
| ||||
| Декартовы координаты на плоскости. Уравнение прямой. Координаты середины отрезка. Формула расстояния между двумя точками плоскости. Уравнение окружности | Объяснять и иллюстрировать понятие декартовой системы координат. Выводить и использовать формулы координат середины отрезка, расстояния между двумя точками плоскости, уравнения прямой и окружности. Выполнять проекты по темам использования координатного метода при решении задач на вычисления и доказательства | Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни. Иметь первоначальные представления об идеях и о методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов | ||
| ||||
| Вектор. Координаты вектора на плоскости. Длина (модуль) вектора. Равенство векторов. Угол между векторами. Операции над векторами: умножение вектора на число, сложение, скалярное произведение | Формулировать определения и иллюстрировать понятия вектора, длины (модуля) вектора, коллинеарных векторов, равных векторов. Вычислять длину и координаты вектора. Находить угол между векторами. Выполнять операции над векторами. Выполнять проекты по темам использования векторного метода при решении задач на вычисления и доказательства | Умение понимать и использовать математические средства наглядности. Умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера; | ||
| Резерв времени - 10ч | ||||
VII. Описание учебно-методического и материально-технического обеспечения образовательного процесса
Оснащение процесса обучения математике обеспечивается библиотечным фондом, печатными пособиями, а также информационно-коммуникативными средствами, экранно-звуковыми пособиями, техническими средствами обучения, учебно-практическим и учебно-лабораторным оборудованием.
В библиотечный фонд входят Стандарт по математике, примерные программы, авторские программы, комплекты учебников, рекомендованных или допущенных Министерством образования и науки Российской Федерации. В состав библиотечного фонда входят рабочие тетради, дидактические материалы, сборники контрольных и самостоятельных работ, практикумы по решению задач, соответствующие используемым комплектам учебников; сборники заданий, обеспечивающих диагностику и контроль качества обучения в соответствии с требованиями к уровню подготовки выпускников, закрепленными в Стандарте по математике; учебная литература, необходимую для подготовки докладов, сообщений, рефератов, творческих работ.
В комплект печатных пособий включены таблицы по математике, в которых представлены правила действий с числами, таблицы метрических мер, основные сведения о плоских и пространственных геометрических фигурах, основные математические формулы, соотношения, законы, графики функций.
Информационные средства обучения - мультимедийные обучающие программы и электронные учебные издания, ориентированные на систему дистанционного обучения либо имеющие проблемно-тематический характер и обеспечивающие дополнительные условия для изучения отдельных тем и разделов Стандарта. Эти пособия предоставляют техническую возможность построения системы текущего и итогового контроля уровня подготовки учащихся (в том числе в форме тестового контроля). Инструментальная среда предоставляет возможность построения и исследования геометрических чертежей, графиков функций, проведения числовых и вероятностно-статистических экспериментов.
Минимальный набор учебного оборудования включает:
Библиотечный фонд
-
-нормативные документы: Примерная программа основного общего образования по математике, Планируемые результаты освоения программы основного общего образования по математике; -
-авторские программы по курсам математики; -
-учебники: по математике для 5-6 классов, по алгебре и геометрии для 7-9 классов; -
-учебные пособия: рабочие тетради, дидактические материалы, сборники контрольных работ; -
-пособия для подготовки и/или проведения государственной аттестации по математике за курс основной школы; -
-учебные пособия по элективным курсам; -
-научная, научно-популярная, историческая литература; -
-справочные пособия (энциклопедии, словари, справочники по математике и т.п.); -
-методические пособия для учителя.