Файл: Интернет вещей безопасность Основные принципы, методы. Безопасности цифровой судебной экспертизе.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 103
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ассоциация управляет на основе различных параметров с поддержкой (10%, 20%, 30%... 100%), и уверенность (80%, 90% и 100%), и некоторые обсуждены подробно.
1. Поддерживайте 90%, количество 90% уверенности правил = 1
(только параметр P12)
2. Поддерживайте 90%, количество 80% уверенности правил = 1
(Только параметр P12)
3. Поддерживайте 80%, количество 90% уверенности правил = 1
(Только параметр P12)
4. Поддерживайте 80%, количество 80% уверенности правил = 1
(Только параметр P12)
5. Поддерживайте 70%, количество 90% уверенности правил = 3
(Параметр правила 1 P12, правило 2 P12, связанное с P14 и параметром правила 3 P12, связанный с P13)
6. Поддерживайте 70%, количество 80% уверенности правил = 3
(Параметр правила 1 P12, правило 2 P12, связанное с P14 и параметром правила 3 P12, связанный с p13)
7. Поддерживайте 60%, количество 90% уверенности правил = 4
(P12, P12 ^ P15, P12 ^ P14, P12 ^ P13)
8. Поддерживайте 60%, количество 80% уверенности правил = 7
(P12, P14 ^ P15, P13 ^ P15, P12 ^ P15, P12 ^ P14, P12 ^ P13, P14 ^ P15 P12)
9. Поддерживайте 50%, количество 90% уверенности правил = 7
(P12, P12 ^ P15, P12 ^ P14, P12 ^ P13, P12 ^ P15 P14, P12 ^ P15 P13, P12 ^ P14 P13)
10. Поддерживайте 50%, количество 80% уверенности правил = 7
(P12, P12 ^ P15, P12 ^ P14, P12 ^ P13, P12 ^ P15 P14, P12 ^ P15 P13, P14 P13 P12 ^) поддержка (%)
1
2
3
4
5
10
20
30
40
50
60
70
80
90
100
Размер ARM (5/80%)
16
16
15
15
13
10
7
3
2
1
1
1
1
1
1
Размер ARM (10/80%)
2730
2730
2083
1185
827
81
13
5
2
1
1
1
1
1
1
Размер ARM (15/80%)
184,228
184,228
140,996
67,472
29,995
1479
201
60
20
16
12
11
4
4
3
Размер ARM (20/80%)
9,023,784
9,023,784
5,173,132
934,992
243,482
4326
349
101
44
36
22
11
4
4
3
Размер ARM (22/80%)
62,151,312
25,389,899
5,619,616
407,512
145,504
1995
118
39
15
11
7
3
1
1
0
Размер ARM (5/90%)
16
16
15
15
13
10
7
3
2
1
1
1
1
1
1
Размер ARM (10/90%)
2262
2262
1615
717
359
59
13
5
2
1
1
1
1
1
1
Размер ARM (15/90%)
8,864,766
8,864,766
5,014,114
775,884
84,464
2176
181
59
36
28
16
11
4
4
3
Размер ARM (20/90%)
8,864,766
8,864,766
5,014,114
775,884
84,464
2176
181
59
36
28
16
11
4
4
3
Размер ARM (22/90%)
62,050,814
25,289,401
5,519,118
307,014
45,006
734
35
14
9
7
4
3
1
1
0
Размер ARM (5/100%)
16
16
15
15
13
10
7
3
2
1
1
1
1
1
1
Размер ARM (10/100%)
2252
2252
1605
707
349
49
13
5
2
1
1
1
1
1
1
Размер ARM (15/100%)
166,558
166,558
123,326
49,802
12,325
439
65
22
10
8
6
5
2
2
1
Размер ARM (20/100%)
8,863,626
8,863,626
5,012,974
774,744
83,324
1036
97
33
18
14
8
5
2
2
1
Размер ARM (22/100%)
62,050,212
25,288,799
5,518,516
306,412
44,404
132
0
0
0
0
0
0
0
0
0
Таблица 6.13 Эффект вариации в размере параметра (от 5, 10, 15, 20, и 22) с переменной поддержкой (в уверенности - 80%, 90% и 100%) и соответствующее количество правил ассоциации [Категория-B]
120 Загадочной Горной промышленности для основанной на AVK Системы шифрования партии
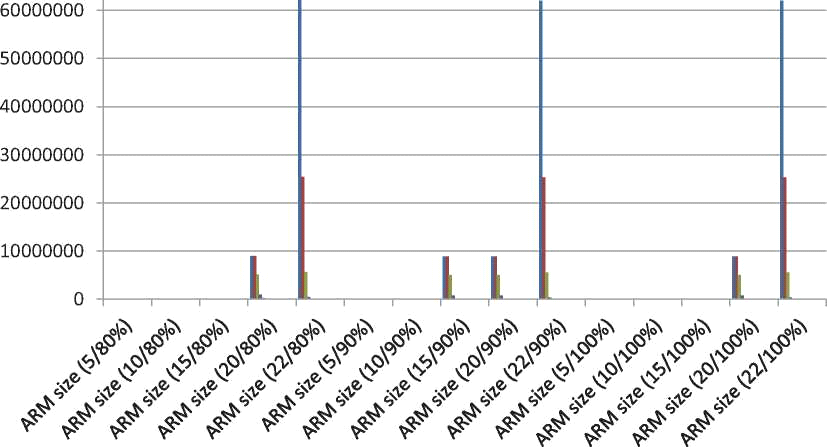
■ 1
■ 2
3
■ 4
■ 5
■ 10
■ 20
■ 30
■ 40
■ 50
■ 60
■ 70
Рисунок 6.2 Эффект вариации в размере параметра (от 5, 10, 15, 20, и 22) с переменной поддержкой (в уверенности - 80%, 90% и 100%) и соответствующее количество правил ассоциации. Поддержка
(%)
1
2
3
4
5
10
20
30
40
50
60
70
80
90
100
Время
(5/80%)
0.12
0.02
0.05
0.05
0.05
0.01
0.05
0.05
0.05
0.05
0.05
0.05
0.05
0.05
0.05
Время (10/80%)
0.04
0.04
0.04
0.04
0
0
0
0
0
0
0
0
0
0
0
Время (15/80%)
0.17
0.19
0.13
0.06
0.03
0.05
0.04
0
0.06
0.04
0
0
0
0
0
Время
(20/80%)
9.83
9.88
5.36
0.12
0.25
0.01
0
0
0
0
0
0
0
0
0
Время (22/80%)
108.27
27.21
5.67
0.46
0.15
0.02
0.01
0.01
0.01
0.01
0.01
0.01
0.01
0.01
0
Время
(5/90%)
0.02
0.02
0.05
0.05
0.05
0.01
0.05
0.05
0.05
0.05
0.05
0.05
0.05
0.05
0.05
Время (10/90%)
0.04
0.04
0.04
0.04
0
0
0
0
0
0
0
0
0
0
0
Время
(15/90%)
0.16
0.16
0.12
0.05
0.02
0.06
0.04
0
0.06
0.04
0
0
0
0
0
Время (20/90%)
9.61
9.51
5.26
0.77
0.08
0
0
0
0
0
0
0
0
0
0
Время
(22/90%)
70.94
29.34
5.63
0.3
0.09
0.02
0.01
0.01
0.01
0.01
0.01
0.01
0.01
0.01
0
Время (5/100%)
0.02
0.02
0.05
0.05
0.05
0.04
0.05
0.05
0.05
0.05
0.05
0.05
0.05
0.05
0.05
Время (10/100%)
0.04
0.04
0.04
0.04
0
0
0
0
0
0
0
0
0
0
0
Время (15/100%)
0.16
0.16
0.19
0.05
0.01
0
0
0
0
0
0
0
0
0
0
Время (20/100%)
9.59
9.55
5.23
0.78
0.1
0
0
0
0
0
0
0
0
0
0
Время (22/100%)
71.91
28.41
5.62
0.3
0.06
0.01
0
0
0
0
0
0
0
0
0
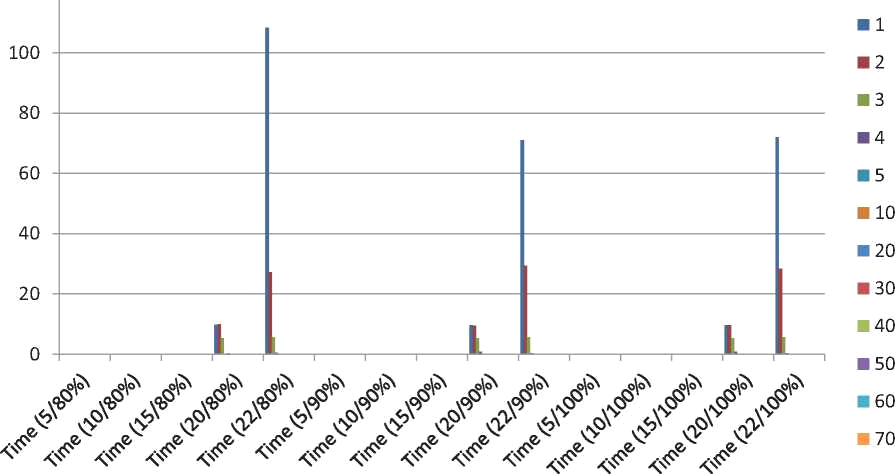
Таблица 6.14 Изменение поддержки и уверенности и время для поколения правил ассоциации (с 22 параметрами) [Категория C]
122 Загадочной Горной промышленности для основанной на AVK Системы шифрования партии
120
Рисунок 6.3 Изменение поддержки и уверенности и время для поколения правил ассоциации (с 22 параметрами).
6.5 Анализ загадочных результатов горной промышленности параметрической модели 123
6.5.1 Наблюдение для Горной промышленности правил ассоциации (ARM)
1. Правила показывают возможность выбора комбинации параметра и относительно их корреляции.
2. Для поддержки меньше чем 10% и уверенности 80% и выше, числа правил высоки в числе, и кардинальность набора объекта является возросшей. Это указывает на возможность выбора подобных параметров для ключа небольшим количеством людей, и комбинации являются слишком большими для оценки.
3. С поддержкой, больше, чем 10% и меньше чем 40%, и уверенностью 80% и выше, количество правил рационально, но нуждается в строгих усилиях оценить. Однако его полноценность сомнительна, как много параметров вне соображения из-за высокой поддержки.
4. С поддержкой, больше, чем 40% и доверительным уровнем больших, чем или равный 80%, хотя правила - очень немногие и ограничили параметры, легко оценить, но в то же время возможности нахождения естественных правил высоки.
Включение криптоаналитика с усовершенствованными инструментами всегда пользуется спросом для идентификации слабости и дальнейшего совершенствования системы шифрования. В полиномиальное время криптоаналитик интересуется извлечением полезных предположений для обнаружения исходной информации из огромного корпуса шифров. Криптоаналитик, возможно, получил большую базу данных и корпус, содержащий множество файлов хеша и шифров. Когда шифрованный текст вставляется в этот набор данных, он мог бы быть смешан в других шифрах, сгенерированных из различных других схем, включая вариации в размере ключа, протоколе, типе алгоритма поколения шифра,
степени воздействия информации, касавшейся ключевого пространства и большой другой информации, связанной с простым текстом, шифрованным текстом и отношениями между ними. Криптоаналитик может разработать механизм, который классифицирует, отсортирует, и группа согласно типу шифра.
6.6 Заключение
Успех любого приложения IoT полагается на безопасность связанной информации и их сред тестирования. Разработать более защищенный и защищенный от нападения IoT - включило информационную систему, более определенные криптографические подходы необходимы. Кроме того, поиск данных и обработка являются неотъемлемыми частями целой ОСНОВАННОЙ НА IOT информационной системы, которая должна быть защищена посредством высокоуровневого шифрования. Более усовершенствованные беспроводные протоколы со строгими ключами доступны для развертывания безопасности IoT. Один такой подход основан на использовании AVK, который обсужден в этой главе с подробным анализом с вариацией в поддержке и уверенности. Хотя даже после использования схемы оптимального шифрования, устройство или сеть системы IoT останутся уязвимыми против нападений. Если нет никакого способа установить подлинность данных, переданных к и от устройства IoT, безопасность может, конечно, быть поставлена под угрозу. Для решения этого вопроса схемы AVK могут быть полезны для создания. Предложенная модель была протестирована и проанализирована с несколькими параметрами, количеством частых наборов и количеством правил ассоциации, которые будут сгенерированы. Предложенная основанная на AVK параметрическая модель удобна для пользователя и все же более тверда с загадочных точек зрения горной промышленности.
Ссылки
[1] Chakrabarti P., Bhuyan B., Chowdhuri A., и Bhunia C., новый подход к пониманию оптимальной передачи данных и Ключа автоматической переменной (AVK) в криптографии. IJCSNS. 8, 241, 2008.
[2] Chakrabarti, P., Bhuyan, B., Chowdhuri, A. и Bhunia, C. T., “Приложение. Ключ автоматической переменной (AVK) в RSA”, в Int’lJ транзакции ХИТА на ECCN, 2, 304-311, 2007.
[3] Chakrabarti, P., Mondal, G. H., Bhunia, C. T. и Chowdhuri, A., Различные Новые и Измененные подходы для выборочного шифрования (DES, RSA и AES) с AVK и их сравнительным исследованием. Интервал J. Сделка ECCN, 1 (4), 236-244, 2008.
[4] Bhunia, C. T., Приложение AVK и выборочного шифрования в улучшении производительности квантовой криптографии и сетей, Организация Объединенных Наций Образовательная Научная и Культурная Организация и Международное агентство по атомной энергии
, 10, 200-210, 2006.
[5] Dutta, M. P., Banerjee, S. и Bhunia, C., “Два Новых Плана Генерировать Ключ автоматической переменной (AVK) для достижения Идеальной безопасности в Небезопасном Канале передачи”, в Продолжениях Международной конференции 2015 года по вопросам Перспективного исследования в Разработке Информатики и Технологии (ICARCSET 2015), 1-4, 2015.
[6] Bhunia, C. T., Chakrabarti, P., Chowdhuri, A. и Чандан, T., реализация ключа автоматической переменной с теорией Choas и изученный этого, J. Наука аккомпанемента IUP 5, 22-32, 2011.
[7] Bhunia, C. T., Mondal, G. и Samaddar, S., “Теории и Приложение Ключа Варианта Времени в RSA и этом с выборочным шифрованием в AES”, в материалах EAIT, Публикации Elsevier, Калькутта CSI-06, 219-221, 2006.
[8] Bhunia, C. T., Chakrabarti, P., Goswami, R., “Новая техника (CSAVK) ключа автоматической переменной в достижении идеальной безопасности”, 100-й индийский научный Конгресс ассоциация, 2013.
[9] Bhunia, C. T., Новые Подходы для Выборочной AES к Дорожке - Эффект Передачи ошибок морского налима AES. Азия. J. Сообщить. Технол 5, 1017-1022, 2006.
[10] Ханьцы, J., Kamber, M. и Pei, J., Анализ данных: Понятия и Техника, 2-й edn, Morgan Kaufmann, 2006.
[11] Prajapat, S. и Thakur, R. S., Загадочная Горная промышленность: Анализ Apriori Параметризованного Ключа Автоматической переменной основывал Симметричную Систему шифрования. Интервал J. Наука аккомпанемента Сообщает. Secur. 14, 233-246, 2016.
[12] Prajapat, S., Rajput, D. и Thakur, R. S., “Подход варианта времени к симметричному ключу”, в Продолжениях Науки IEEE и информационной Конференции (САЙ), Лондон 2013, 398-405, 2013.
[13] Prajapat, S. и Thakur, R. S.. “Оптимальный размер ключа AVK для шифрования с симметричным ключом”, в журнале соглашения информационно-коммуникационных технологий, 3 (2), 71-81, 2015.
[14] Prajapat, S., Thakur, R. S., различные подходы к криптоанализу. Интервал J. Аккомпанируйте прикладной 127 (14), 15-24, 2015.
[15] Prajapat, S., Thakur, R. S., загадочная горная промышленность для автоматической переменной основанная на ключе система шифрования. ElsevierProcediaComp. Sci. 78 (78C), 199-209, 2016.
[16] Prajapat, S., Thakur, R. S., Реализация обмена информацией с Fibo-Q основывала Симметричную Систему шифрования. Интервал J. Наука аккомпанемента Сообщает. Secur. 14 (2), 216-223, 2016.
[17] Prajapat, S., Thakur, A., Maheshwari, K. и Thakur, R. S., загадочная горная промышленность в свете искусственного интеллекта. IJACSA 6 (8), 62-69, 2015. Глоссарий
Числа
51%-е Нападение
Когда больше чем половиной вычислительной мощности сети криптовалюты управляют единственный объект или группа, этот объект или группа могут выпустить конфликтующие