Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательное учреждениевысшего образования«Уфимский государственный нефтяной технический университет»Кафедра автоматизации технологических процессов и производствКурсовая работапо курсу«Метрология, стандартизация и сертификация»Вариант №3Зачетная книжка № ----83Выполнил: студ. гр. БАГи-17-01 Проверил: к. т. н., доцент Э.А. Шаловников Уфа 2019СОДЕРЖАНИЕ

1. 
   Обработка результатов прямых равноточных видов измерений……… 3
   
2. 
   Обработка косвенных видов измерений………………………………….7
   
3. 
   Нормирование метрологических характеристик (МХ) средств измерений (СИ) классами точности……………………………………. 16
   
4. 
   Методика расчёта статистических характеристик погрешностей СИ в эксплуатации. Определение класса точности…………………………...20
   
5. 
   Методика построения функциональных схем автоматизации технологических процессов………………………………………………...23
   
6. 
   Список использованных источников……………………………………25
   
7. 
   Приложение……………………………………………………………….26
   

1 Обработка результатов прямых равноточных видов измеренийИсходные данные:0,111; 0,085; 0,091; 0,101; 0,109; 0,086; 0,102; 0,111; 0,098; 0,085; 0,105; 0,112;0,098; 0,113; 0,087; 0,109; 0,115; 0,099; 0,099; 0,094; 0,105.А Точечная оценкаРанжируем исправленный ряд результатов:

0,085	0,085	0,086	0,087	0,091	0,094	0,098	0,098	0,099	0,099	0,101
0,102	0,105	0,105	0,109	0,109	0,111	0,111	0,112	0,113	0,115

---

Находим среднее арифметическое 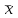: 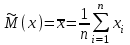= 0,100714Определим оценку среднего квадратического отклонения (с. к. о.):а) Оценка с. к. о. отдельного результата наблюдения (формула Бесселя): 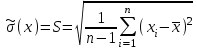= = 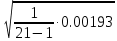0,00982. б) Оценка с. к. о. среднего арифметического 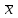: 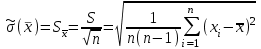= = 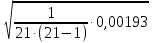0,00214. Б Критерии грубых погрешностейКритерий Грабса или n – критерий: 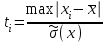= = 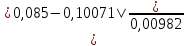1,60038 при x_i = 0,085.t_Г = f (q; k) = f (5%; 20) = 2,779. (табл. 1.3)где q=1 - p_Д = 1- 0,95=0,05=5% - уровень значимости;k=n-1=21-1=20 – число степеней свободы.Получаем, что t_i< t_Г, значит, грубых погрешностей нет и расчет продолжается.Записываем результаты точечной оценкиВ Интервальная оценкаОценим доверительный интервал математического ожидания 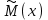:Воспользуемся формулой Петерса: 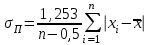= 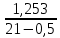∙ 0,17029 = 0,01041,т.к. 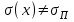, то воспользуемся распределением Стьюдента: 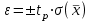= 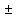2,09∙0,00214= 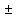0,0045.где t_p = f(q; k)= f(5%; 20)= 2,09. (таблица 1.4)Оценим доверительный интервал с. к. о. 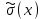(доверительную вероятность возьмем равной 0.9):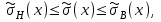

---

где 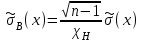= 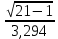∙ 0,00982= 0,013, где c²_Н = f (k; q_Н) = f (20; 95%) = 10,851, т.е. 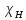= 3,294, т.к. q_Н = 1– p_Н = 1 - (1 – p_Д)/2 = 1 – (1-0,9)/2 = 0,95 = 95%. 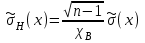= 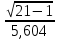∙ 0,00982=0,008,где c²_В = f (k; q_В) = f (20; 5%) = 31,410, т.е. 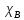= 5,604, т.к. q_В = 1– p_В = 1 - (1 + p_Д)/2 = 1 – (1+0,9)/2 = 0,05 = 5%.Записываем результаты измерения: 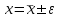, при p_Д = 0,95, при p_Д = 0,9.Итак, X = 0,1007 0,0045, при p_Д = 0,95,0,008≤ 0,010≤ 0,013, при p_Д = 0,9.Свойства математического ожидания и дисперсииПри измерении случайной величины θ с математическим ожиданием М(θ)и дисперсией D(θ) получен следующий ряд результатов:

0,085	0,085	0,086	0,087	0,091	0,094	0,098	0,098	0,099	0,099	0,101
0,102	0,105	0,105	0,109	0,109	0,111	0,111	0,112	0,113	0,115

Каждый результат уменьшается на одно и то же постоянное число a и умножается на один и тот же постоянный множитель b. Получается cлучайная величина 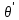и вычисляется по формуле: =(

---

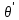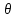
-a)·b

В качестве постоянного числа можно взять a = 0,100, а b = 1000 (для удобства расчета), тогда получим другой ряд результатов для :

-15	-15	-14	-13	-9	-6	-2	-2	-1	-1	1
2	5	5	9	9	11	11	12	13	15

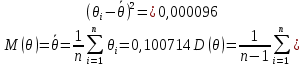
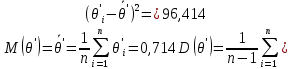
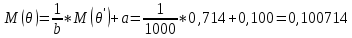
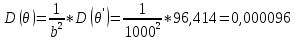
Найдем математическое ожидание и дисперсию для изначального ряда исходя из определения этих величин:Посчитаем математическое ожидание и дисперсию для полученного ряда, исходя из определения этих величин:Исходя из первого и второго свойств математического ожидания и дисперсии, определяются M(θ) и D(θ) для исходного ряда:M(θ’)=M[(θ-a)·b]=b·[M(θ)-a];D(θ’)=D[(θ-a)·b]=b²·D(θ-a)=b²·D(θ); Значения математического ожидания и дисперсии, вычисленные по определению и по свойствам – совпадают. Таким образом, была доказана верность свойств математического ожидания и дисперсии.Таблица 1.1 – Результаты расчётов Х1

Исходные данные	Результаты расчёта	Комментарии
X1, n=21	Точечная оценка
0,085	0,100714	среднее арифметическое
0,085	0,009819	оценка с.к.о. (ф. Бесселя)
0,086	0,002143	оценка с.к.о. среднего арифметического
0,087	Критерий грубых погрешностей
0,091	0,115	Xmax
0,094	0,085	Xmin
0,098	1,454894	t2
0,098	1,600383	t1
0,099	2,779	tr = f(q,n) = f(5%,18) - таблица 1.3
0,099	т.к. tr ≥t2 и tr≥t1, то грубых погрешностей нет, расчет продолжаем
0,101	Интервальная оценка МО
0,102	0,0081088435	среднее абсолютных отклонений
0,105	0,1702857143	сумма абсолютных отклонений
0,105	0,0104081951	ф. Петерса
0,109	если ф. Бесселя = ф. Петерса, то закон распределения нормальный
0,109	1,9599639845	t
0,111	0,0192450385	доверительный интервал
0,111	если ф. Бесселя ≠ ф. Петерса, то распределение Стьюдента
0,112	2,0859634473	tp
0,113	0,0044695906	доверительный интервал
0,115	Интервальная оценка с.к.о.
	31,4104328442	χ2в
	10,8508113942	χ2н
	0,0072236749	с.к.о. нижнее
	0,0122903442	с.к.о. верхнее
	Результаты расчёта
	X=0,1007±0,0045 при Pд=0,95
	0,008≤0,010≤0,013 при Рд=0,9

---

Таблица 1.2 – Описательная статистика X₁

Среднее	0,100714286
Стандартная ошибка	0,002142698
Медиана	0,101
Мода	0,085
Стандартное отклонение	0,009819078
Дисперсия выборки	9,64143E-05
Эксцесс	-1,122458731
Асимметричность	-0,298568002
Интервал	0,03
Минимум	0,085
Максимум	0,115
Сумма	2,115
Счет	21
Наибольший(1)	0,115
Наименьший(1)	0,085
Уровень надежности(95,0%)	0,004469591

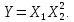
2 Обработка косвенных видов измеренийИсходные данные: Х₁0,111; 0,085; 0,091; 0,101; 0,109; 0,086; 0,102; 0,111; 0,098; 0,085; 0,105; 0,112;0,098; 0,113; 0,087; 0,109; 0,115; 0,099; 0,099; 0,094; 0,105.Х₂29,28; 28,88; 29,29; 29,23; 29,1; 28,95; 29,1; 29,2; 29,03; 29,07; 28,5;29,19; 29,2; 29,17; 29,12;29,15; 29,09; 29,04.Уравнение связи:Расчет первого аргумента Х₁ уже был произведен.Произведем расчет второго аргумента X₂.А Точечная оценка 2.1 Ранжированный исправленный ряд результатов X₂, n=18.

28,5	28,88	28,95	29,03	29,04	29,07	29,09	29,1	29,1
29,12	29,15	29,17	29,19	29,2	29,2	29,23	29,28	29,29

---

Смотрите также файлы

• Реферат Закаливание один способов зож.docx

• Интернет вещей безопасность Основные принципы, методы. Безопасности цифровой судебной экспертизе.doc

• Экзаменационная ведомость (предварительная,экзамен автомат).docx

• Выпускная квалификационная работа методика обучения морфемному составу слова.docx

• Депрессивные состояния во время кризиса подросткового возраста Содержание.odt