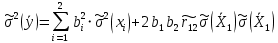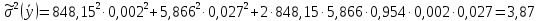2.2 Среднее арифметическое 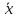: =29,092.3 Оценка среднего квадратического отклонения (с. к. о.):а) Оценка с. к. о. отдельного результата наблюдения (формула Бесселя): = =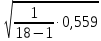0,1814б) Оценка с. к. о. среднего арифметического 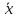: = =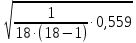 0,04275Б Критерии грубых погрешностей2.4 Критерий Грабса или n – критерий:t₁= 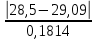= 3,244 при x = 28,5t₂= 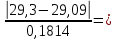1,112 при x = 29,3t_Г = f (q; n ) = f (5%; 18) = 2,728, где q=1 - p_Д = 1- 0,95=0,05=5% - уровень значимости;n=18 – число наблюдений.Критерий не выполняется т.к. t₂ < t_Г , t₁ > t_Г. Результат 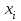=28,5 как промах отбрасываем и расчеты повторяем при новом числе наблюдений n=17.

	28,88	28,95	29,03	29,04	29,07	29,09	29,1	29,1
29,12	29,15	29,17	29,19	29,2	29,2	29,23	29,28	29,29

=29,12 = =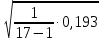0,10976 = =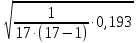 0,0266

---

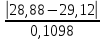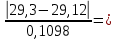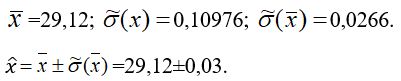
t₁= = 2,213 при x = 28,88t₂= 1,522 при x = 29,3t_Г = f (q; n ) = f (5%; 17) = 2,701, где q=1 - p_Д = 1- 0,95=0,05=5% - уровень значимости;n=17 – число наблюдений.Критерий выполняется т.к. t_i< t_Г .Грубых погрешностей нет и расчет продолжается.Записываем результаты точечной оценкиВ Интервальная оценка2.5 Доверительный интервал математического ожидания :По формуле Петерса определяется закон распределения случайных результатов: = 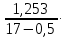1,453 = 0,1103т.к. , то воспользуемся распределением Стьюдента: = 2,12 0,1098= 0,056где t_p = f(q; k)= f(5%;16)=2,12.2.6 Доверительный интервал с. к. о. (p_Д = 0.9):q_Н= 1– p_Н = 1 - (1 – p_Д)/2 = 1 – (1-0,9)/2 = 0,95 = 95%.c²_Н = f (k; q_Н) = f (16; 95%) = 7,962, т.е. = 2,8217, = 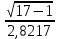∙ 0,1098= 0,169, q_В= 1– p_В = 1 - (1 + p_Д)/2 = 1 – (1+0,9)/2 = 0,05 = 5%.c²_В = f (k; q_В) = f (16; 5%) = 26,296, т.е. = 5,128, = 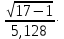0,1098=0,0862.7 Результаты измерения: , при p_Д = 0,95,

---

при p_Д = 0,9.

X = 29,12 0,06, при p_Д = 0,95,

0,09 ≤ 0,11 ≤ 0,17, при p_Д = 0,9.
Свойства математического ожидания и дисперсии
При измерении случайной величины θ с математическим ожиданием М(θ)и дисперсией D(θ) получен следующий ряд результатов:

28,88	28,95	29,03	29,04	29,07	29,09	29,1	29,1	29,12
29,15	29,17	29,19	29,2	29,2	29,23	29,28	29,29

Каждый результат уменьшается на одно и то же постоянное число a и умножается на один и тот же постоянный множитель b. Получается cлучайная величина и вычисляется по формуле: =( -a)·bВ качестве постоянного числа можно взять a = 29,08, а b = 100 (для удобства расчета), тогда получим другой ряд результатов для :

-20	-13	-5	-4	-1	1	2	2	4
7	9	11	12	12	15	20	21

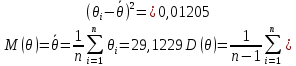
Найдем математическое ожидание и дисперсию для изначального ряда исходя из определения этих величин:Посчитаем математическое ожидание и дисперсию для полученного ряда, исходя из определения этих величин:

---

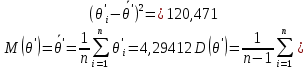
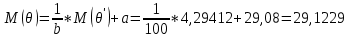
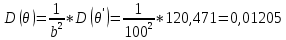
Исходя из первого и второго свойств математического ожидания и дисперсии, определяются M(θ) и D(θ) для исходного ряда:M(θ’)=M[(θ-a)·b]=b·[M(θ)-a];D(θ’)=D[(θ-a)·b]=b²·D(θ-a)=b²·D(θ); Значения математического ожидания и дисперсии, вычисленные по определению и по свойствам – совпадают. Таким образом, была доказана верность свойств математического ожидания и дисперсии.Таблица 2.1 – Результаты расчета X₂

Исходные данные	Результаты расчёта	Комментарии
X2, n=17	Точечная оценка
28,88	29,12	среднее арифметическое
28,95	0,109759094	оценка с.к.о. (ф. Бесселя)
29,03	0,026620491	оценка с.к.о. среднего арифметического
29,04	Критерий грубых погрешностей
29,07	29,29	Xmax
29,09	28,88	Xmin
29,1	1,52204994	t2
29,1	2,21340361	t1
29,12	2,701	tr = f(q,n) = f(5%,17) - таблица 1.3
29,15	т.к. tr ≥t2 и tr≥t1, то грубых погрешностей нет, расчет продолжаем
29,17	Интервальная оценка МО
29,19	0,085	среднее абсолютных отклонений
29,2	1,453	сумма абсолютных отклонений
29,2	0,110335	ф. Петерса
29,23	если ф. Бесселя = ф. Петерса, то закон распределения нормальный
29,28	1,9599639845	t
29,29	0,2151238722	доверительный интервал
	если ф. Бесселя ≠ ф. Петерса, то распределение Стьюдента
	2,1199052992	tp
	0,0564329191	доверительный интервал
	Интервальная оценка с.к.о.
	26,2962276049	χ2в
	7,9616455724	χ2н
	0,0856157729	с.к.о. нижнее
	0,1695570671	с.к.о. верхнее
	Результаты расчёта
	X=29,12±0,06 при Pд=0,95
	0,09≤0,11≤0,17 при Рд=0,9

---

Таблица 2.2 – Описательная статистика X2

Среднее	29,12294118
Стандартная ошибка	0,026620491
Медиана	29,12
Мода	29,1
Стандартное отклонение	0,109759094
Дисперсия выборки	0,012047059
Эксцесс	0,185969635
Асимметричность	-0,535060748
Интервал	0,41
Минимум	28,88
Максимум	29,29
Сумма	495,09
Счет	17
Наибольший(1)	29,29
Наименьший(1)	28,88
Уровень надежности(95,0%)	0,056432919

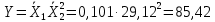
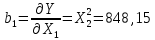
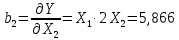
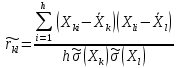
Возвращаемся к обработке косвенных видов измерений:Исходя из уравнения связи, оценим искомый результат:Найдем коэффициенты влияния:Оценка коэффициента корреляции между каждой парой аргументов определяется по формуле: где h - наименьшее из чисел наблюдений аргументов 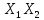. h =17 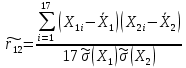= 0,954

---

Смотрите также файлы

• Реферат Закаливание один способов зож.docx

• Интернет вещей безопасность Основные принципы, методы. Безопасности цифровой судебной экспертизе.doc

• Экзаменационная ведомость (предварительная,экзамен автомат).docx

• Выпускная квалификационная работа методика обучения морфемному составу слова.docx

• Депрессивные состояния во время кризиса подросткового возраста Содержание.odt