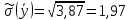
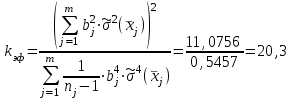
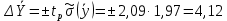
Находится эффективное число степеней свободы выборок двух аргументов X1 и X2Оценим погрешность искомого результата:где t_p=f(q;k_эф), q=1- Р_Д = 0,05. t_p= 2,09Окончательный результат записываем в виде: 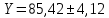при Р_Д =0,95Таблица 2.3 – Результаты расчёта

Косвенный вид	Комментарий
85,42038864	Искомый результат Y
848,15	b1
5,866192437	b2
0,953610914	Коэффициент корреляции r
3,868298775	Оценка дисперсии искомого результата σ2
16,23640945	Эффективное число степеней свободы 2-х выборок k
2,119905299	Коэффициент Стьюдента tp
4,169427875	Погрешность искомого результата ΔY
Результаты расчета
Y=85,42±4,17 при Pд=0,95

2.8 По известной расчетной зависимости косвенного метода измерения (искомый результат) и по известным результатам и погрешностям прямых измерений получить формулу погрешности косвенного измерения.Исходные данные: (вариант 3)

Расчетная зависимость	Погрешности и результаты прямых измерений
y=(b-a)(c+d)/[3e2]	Δa =1 a =50	Δb =3 b =90	Δc =2 c =60	Δd =2 d =70	Δe =1 e =40

---

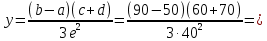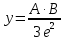
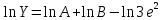
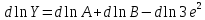
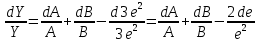
1,0832.8.1 Коэффициенты влияния 1. Введём обозначение A = b – a; B = c + d. Тогда получим:2. Прологарифмируем левую и правую части заданной зависимости:3. Найдём дифференциал правой и левой частей4. Найдем дифференциал от логарифма:5. Произведём широко используемую в теории погрешностей замену дифференциалов малыми абсолютными погрешностями (при условии, что абсолютные погрешности достаточно малы), т.е. dY =∆Y, dA =∆A, de=∆e, dB =∆B. 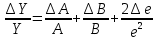А также заменим «-» на «+».Здесь A = b – a; B = c + d, тогда ∆A=∆b + ∆a и ∆B=∆c + ∆d. 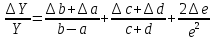Окончательно 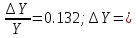0.132*1.083 = 0.143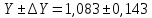

---

3 Нормирование метрологических характеристик (МХ) средств измерений (СИ) классами точности

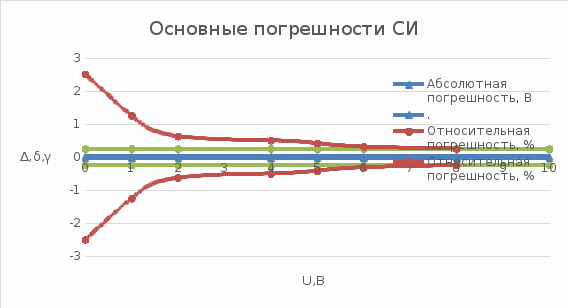
3.1 Для прибора с преобладающими аддитивными погрешностями рассчитать значения абсолютных, относительных и приведенных основных погрешностей измерений. Результаты представить в виде таблицы и графи -ков.Исходные данные:

Вариант 3

Диапазон измерений (0...10) В

Класс точности 0,25

Результаты измерений 0; 1; 2; 4; 5; 6; 8; 10 В

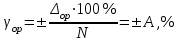
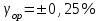
Формулы для расчета:Δ_op= 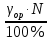,В Δ_op=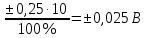

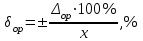
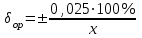
Результаты измерений, В	Абсолютная погрешность, 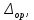В	Относительная погрешность, δop , %	Приведенная погрешность, γop , %
0	±0,025	±∞	±0,25
1	±0,025	±2,5000	±0,25
2	±0,025	±1,2500	±0,25
4	±0,025	±0,6250	±0,25
5	±0,025	±0,5000	±0,25
6	±0,025	±0,4167	±0,25
8	±0,025	±0,3125	±0,25
10	±0,025	±0,2500	±0,25

---

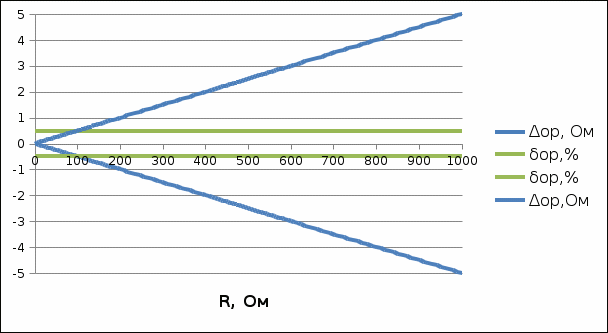
3.2 Для прибора с преобладающими мультипликативными погрешностями рассчитать зависимости абсолютных и относительных основных погреш­ностей от результата измерений. Результаты представить в виде таблицы и графиков.Исходные данные: (Вариант 3)

Класс точности	Результаты измерений
0,5	0; 100; 200; 400; 500; 600; 800; 1000 Ом

Формулы для расчета: 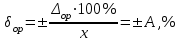δ_op = ± А, % = ±0,5%Δ_op = 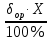, Ом

R, Ом	Δop, Ом	δop,%
0	±0	±0,5
100	±0,5	±0,5
200	±1	±0,5
400	±2	±0,5
500	±3	±0,5
600	±4	±0,5
800	±5	±0,5
1000	0	±0,5

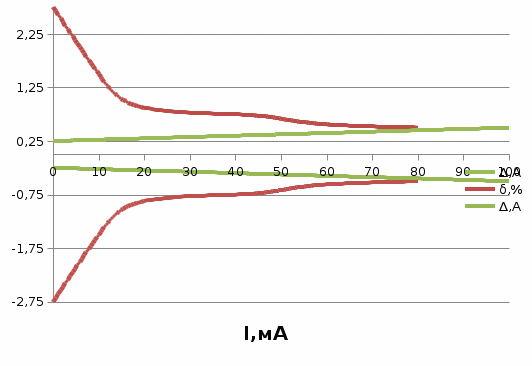
3.3 Для цифрового измерительного прибора рассчитать зависимость абсолютных и относительных основных погрешностей от результата измерений. Результаты представить в виде таблицы и графиков.

Диапазон измерений	Класс точности	Результаты измерений
(-100...+100) мА	0,5/0,25	0; 10; 20; 40; 50; 60; 80; 100 мА

---

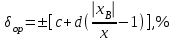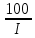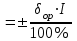Формулы для расчета:δ_ор =(0,5 + 0,25 ( -1)),% Δ_op = , мАΔ_op (0)= 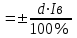, мА Δ_op (0)= 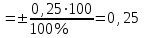мА

I, мА	Δop*10, мА	δop,%
0	±0,25	±∞
10	±0,275	±2,75
20	±0,3	±1,5
40	±0,35	±0,875
50	±0,375	±0,75
60	±0,4	±0,6667
80	±0,45	±0,5625
100	±0,5	±0,5

4. Методика расчёта статистических характеристик погрешностей СИ в эксплуатации. Определение класса точностиИсходные данные: (Вариант 3 (----83))

Р0, кг/м2	РМ, кг/cм2	РБ, кг/cм2	N, кг/cм2
9	8,97	9,15	15
9	8,79	9,07	15
9	8,88	9,01	15
9	8,85	9,14	15
9	8,92	9,02	15
∆м1	-0,03		∆Б1	0,15
∆м2	-0,21		∆Б2	0,07
∆м3	-0,12		∆Б3	0,01
∆м4	-0,15		∆Б4	0,14
∆м5	-0,08		∆Б5	0,02

---

Смотрите также файлы

• Реферат Закаливание один способов зож.docx

• Интернет вещей безопасность Основные принципы, методы. Безопасности цифровой судебной экспертизе.doc

• Экзаменационная ведомость (предварительная,экзамен автомат).docx

• Выпускная квалификационная работа методика обучения морфемному составу слова.docx

• Депрессивные состояния во время кризиса подросткового возраста Содержание.odt