Рис. 11

Первый тип охватывает практически все конденсаторы, второй – электролитические, третий – подстроечные; значение емкости каждого конденсатора может быть установлено в пределах от 10^-8 пФ до 10⁸ Ф. Емкость подстроечного (аналогично потенциометру) конденсатора может изменяться нажатием назначенной пользователем клавиши клавиатуры (по умолчанию – клавиши С), начиная от максимального значения до минимального с заданным шагом (от 1 до 100 %). Все эти установки производятся с помощью диалогового окна.

Резисторы

Резисторы являются самыми массовыми изделиями электронной техники. В программе EWB 5.1. резисторы представлены тремя типами – постоянным, подстроечным, набором из восьми резистором, показанными на рис.12

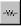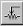Рис. 12

Изменение сопротивления подстроечного резистора осуществляется по тому же принципу, что и для подстроечного конденсатора. В наборе резисторов сопротивление устанавливается одинаковым для всех восьми резисторов.

К основным характеристикам резисторов относятся следующие:

• 
  номинальная мощность – наибольшая мощность, которую резистор может рассеивать в заданных условиях в течение гарантированного срока службы при сохранении параметров в установленных пределах;
  
• 
  рабочее напряжение, при котором резистор может работать, не должно превышать значения, рассчитанного исходя из номинальной мощности и номинального сопротивления;
  
• 
  номинальное сопротивление – электрическое сопротивление, значение которого обозначено на резисторе или указано в нормативной документации.
  

Контрольные вопросы и задания

1. 
   Что относится к элементной базе EWB?
   
2. 
   На какие группы подразделяются источники тока?
   
3. 
   Приведите пример измерительных источников тока?
   
4. 
   Назначение и классификация источников для электропитания?
   
5. 
   Приведите примеры источников для электропитания?
   
6. 
   Охарактеризуйте источники постоянного тока?
   
7. 
   Для чего используются источники тока?
   
8. 
   Что относится к индикаторным приборам?
   
9. 
   Охарактеризуйте лампу накаливания?
   
10. 
    Охарактеризуйте 7-сегментный цифровой индикатор?
    
11. 
    Охарактеризуйте 4-входовый индикатор?
    
12. 
    Перечислите параметры звуковой сигнализации?
    
13. 
    Какие устройства называют коммутационными?
    
14. 
    Перечислите пять параметров, характеризующих коммутационные устройства?
    
15. 
    Приведите примеры коммутационных устройств.
    
16. 
    Объясните принцип работы реле времени?
    
17. 
    Какие типы конденсаторов вы знаете?
    
18. 
    Дайте характеристику всем типам конденсаторов?
    
19. 
    Перечислите типы резисторов?
    
20. 
    Назовите основные характеристики резисторов?
    
21. 
    Определите, какие элементы в программе EWB относятся к индуктивным?
    
22. 
    Используя схему на рис. 13, определите ток I, при котором лампочка L перегорает при различных значениях допустимой мощности
    

---

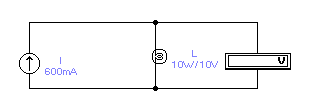
Рис. 13. Применение лампы накаливания в качестве предохранителя.

23. Составьте схему, состоящую из звукового сигнализатора (громкоговорителя), источника постоянного напряжения, резистора, амперметра и вольтметра. Убедитесь в правильности срабатывания звуковой сигнализации при установленных в диалоговом окне значениях тока и напряжения срабатывания.

24. Используя принципы построения схемы на рис. 6, составьте схему, которая бы обеспечивала последовательный во времени (например, через 5с) вывод на индикатор символов 0…9, A…F. Подскажем, что для этого придется добавить еще два ключа.

ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

РЕШЕНИЕ ЗАДАЧ ПО ПЕРВИЧНОЙ ОБРАБОТКЕ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА И ПОДБОРУ ЭМПИРИЧЕСКИХ ФОРМУЛ

Аппроксимация функции. Подбор эмпирических формул.

Приближенная функциональная зависимость y = f(х), полученная на основании экспериментальных данных, называется эмпирической формулой

Построение эмпирической формулы состоит из двух этапов: подбора общего вида этой формулы и определения наилучших значений содержащихся в ней параметров.

Общий вид формулы иногда известен из физических или геометрических соображений. Если характер зависимости неизвестен, то вид эмпирической формулы может быть выбран следующим образом.

Выбор эмпирических формул для нелинейных зависимостей

Пусть y есть функция одной переменной с двумя параметрами а и b. В качестве набора функций, из которых будем выбирать эмпирическую зависимость, рассмотрим:

1	линейную функцию	y = ax+b;
2	показательную функцию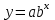
3	дробно-рациональную функцию	y = 1/(ax+b);
4	логарифмическую функцию	y = a*ln(x)+b;
5	степенную функцию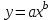
6	гиперболическую функцию	y = a+b/x;
7	дробно-рациональную функцию	y = x/(ax+b).

---

Для наилучшего выбора вида эмпирической зависимости y=f(x,a,b), соответствующей построенному графику, выполним следующие промежуточные вычисления. На заданном отрезке изменения независимой переменной выберем точки, достаточно надежные и по возможности, далеко отстоящие друг от друга. Для простоты будем считать, что это точки x1 и xn.

Вычислим:

среднеарифметическое xар = (x1+xn)/2;

среднегеометрическое xгеом

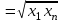
среднее гармоническое xгарм = 2(x1*xn)/(x1+xn).

По вычисленным значениям независимой переменной найдем из построенного графика соответствующие значения зависимой переменной

xар → y1* xгеом → y2* xгарм → y3*

для пока еще неизвестной эмпирической зависимости y = f(x,a,b).

Выполним аналогичные вспомогательные вычисления для зависимой переменной. Вычислим:

среднеарифметическое крайних значений yар = (y1+yn)/2

их среднегеометрическое значение yгеом

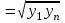
и среднее гармоническое yгарм = 2*(y1*yn)/(y1+yn)

Сравним вычисленные значения yар, yгеом, yгарм с найденными из графика y1*,y2*,y3* и оценим погрешности результата сравнения:

|y1*-yар|= ε1; |y1*-yгеом|= ε2; |y1*-yгарм|= ε3;

|y2*-yар|= ε4; |y2*-yгеом|= ε5; |y2*-yгарм|= ε6;

|y3*-yгарм|= ε7

Найдем из этих ошибок минимальную εmin {ε1, ε2,… ε7}.

- если наименьшей среди всех абсолютных ошибок окажется ε1, то в качестве эмпирической зависимости для данного графика хорошим приближением служит линейная функция y = ax+b

- если наименьшей среди всех абсолютных ошибок окажется ε2, то следует выбирать показательную функцию

- если наименьшей среди всех абсолютных ошибок окажется ε3, то искомая эмпирическая зависимость определяется дробно-рациональной функцией y = 1/(ax+b)

- если наименьшей среди всех абсолютных ошибок окажется ε4, то хорошим приближением служит логарифмическая функция y = a*ln(x)+b

- если наименьшей среди всех абсолютных ошибок окажется ε5, то выбирается степенная функция

- если наименьшей среди всех абсолютных ошибок окажется ε6, то следует выбирать гиперболическую функцию y = a+b/x

- если наименьшей среди всех абсолютных ошибок окажется ε7, то выбирается дробно-рациональная функция вида y = x/(ax+b)

---

Пример. Подобрать эмпирическую зависимость для функции, заданной таблично:

x	1	2	3	4	5	6	7	8	9
y	521	308	240.5	204	183	171	159	152	147

Решение: предположим, что в данном примере крайние табличные значения достаточно надежны: x1 = 1; x9 = 9

1) xар = (x1+x9)/2 = 5

xгеом = 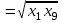= 3

xгарм = 2*(x1*x9)/(x1+x9) = 1.8

2) Построим график функции в соответствии с табличными данными



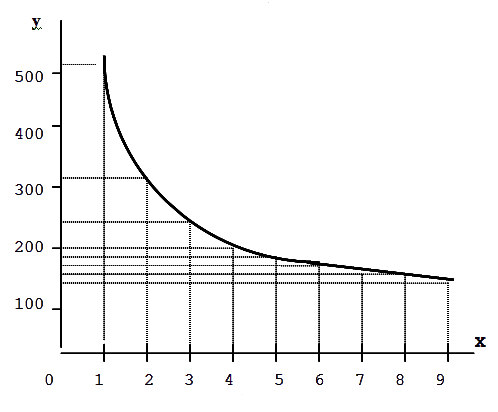
Из графика найдем значения функции, соответствующие вычисленным значениям аргумента

xар → y1* = 180 xгеом → y2* = 240 xгарм → y3* = 341

3)yар = (y1+ yn)/2 = (521+147)/2 = 334

yгеом

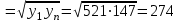
yгарм = 2(y1*yn)/(y1+yn) = 2(521*147)/(521+147)=228

4) Сравним найденные из графика значения зависимой переменной с yар, yгеом, yгарм

1 = y1*-yар = 180-334 = 154

2 = y1*-yгеом = 180-274 = 106

3 = y1*-yгарм = 180-228 = 48

4 = y2*-yар = 240-334 = 94

5 = y2*-yгеом = 240-274 = 34

6 = y3*-yар = 341-334 = 7

7 = y3*-yгарм = 341-228 = 113

Т.к. наименьшая из абсолютных ошибок - 6, то в качестве эмпирической формулы следует выбрать гиперболическую зависимость y=a+b/x.

Преобразование экспериментальных данных методом выравнивания

Если в качестве эмпирической формулы принята нелинейная зависимость (показательная, степенная, дробно-рациональная, гиперболическая, логарифмическая), то, при определении параметров эмпирической зависимости

---

, следует, в соответствии с нижеследующей таблицей, произвести преобразование ее в линейную зависимость, используя метод выравнивания (логарифмируя функцию y=f(x)). Это позволяет существенно упростить расчет, который в результате сводится к решению системы линейных уравнений.

Вид эмпирической формулы	Способ выравнивания
Линейная функция y = ax + b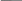
Показательная функция	Y* = A* + B*x, где Y* = lg y;A* = lg a;B* = lg b
Дробно-рациональная функция y = 1/(ax+b)	Y* = ax + b, где Y* = 1/ y
Логарифмическая функция y = a*ln(x)+b	y = aX* + b, где X* = lgx
Степенная функция	Y* = A* + bX*, где Y* = lg y;A* = lg a;X* = lg x
Гиперболическая функция y = a+b/x	Y* = ax + b, гдеY* = x*y
Дробно-рациональная функция y = x/(ax+b)	Y* = ax + b, где Y* = x/ y

Итак, будем считать, что тип эмпирической формулы выбран, и ее можно представить в виде y = (x, ao, a1,…, an) (1)

где - известная функция,

аo, а1,…, аn - неизвестные постоянные параметры.

Здесь не ставится условие (как в случае интерполяции) совпадения опытных данных yi со значениями эмпирической функции (1) в точках xi. Разность между этими значениями (отклонения) обозначим i. Тогда

i =(xi,ao,a1,…,am) – yi, i = 0,1,…,n.

Задача нахождения наилучших значений параметров аo,a1,…,am сводится к некоторой минимизации отклонений 

---

Смотрите также файлы

• Дисциплина Философия.docx

• Описание технологического процесса.docx

• Экономические ресурсы и их виды.docx

• Расчет ректификационной колонны для Разделения бинарной смеси по мдк.docx

• Конкуренция процессного и проектного подхода в качестве инструментов стратегического управления.docx