Добавлен: 23.11.2023
Просмотров: 60
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Нвыхв конце каждого интервала t.
Нвых (∞)= 0.5
Таблица 5.1
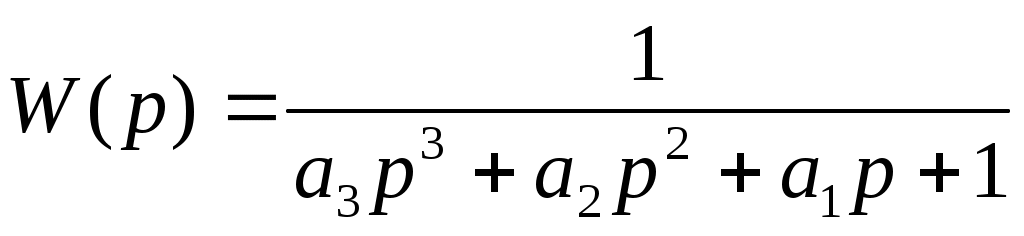
По виду графика определим тип передаточной функции в безразмерном виде:
Задача состоит в том, чтобы определить неизвестные коэффициенты полиномов числителя и знаменателя. Определим площади F1 , F2 , F3для нахождения неизвестных коэффициентов.
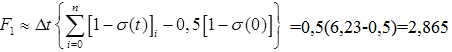
Таким образом, функция приведена к безразмерному виду.
Перестраиваем функцию
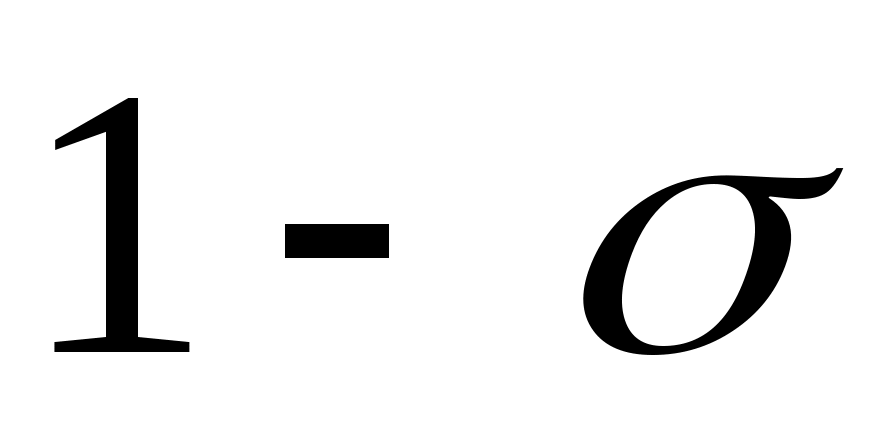в другом масштабе времени (за незави-
симую переменную примем переменную ).
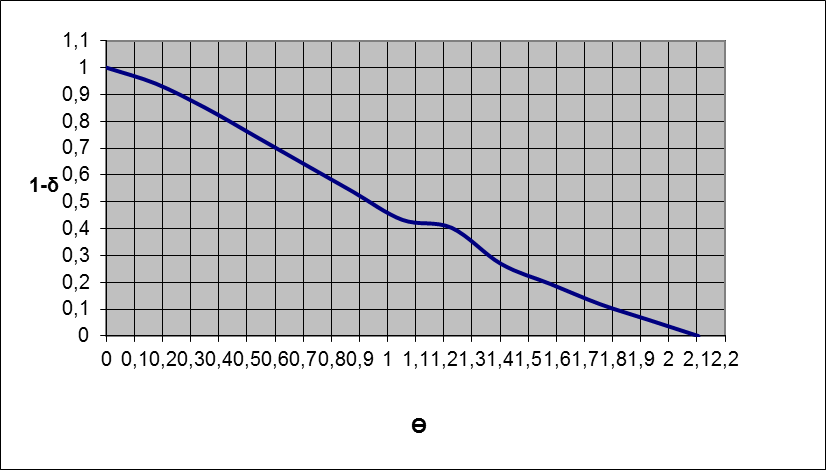
Заполняем таблицу 5.2 и находим коэффициент F2, F3.
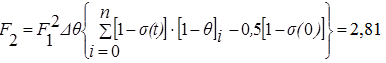
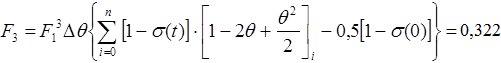
К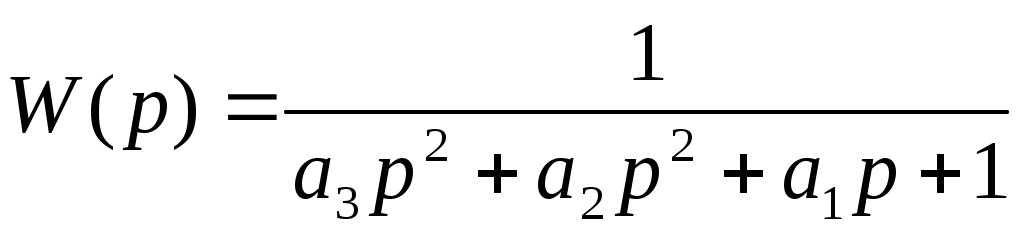
оэффициентом F3 можем пренебречь. Тогда передаточная функция будет иметь вид:
Записываем окончательное выражение исследуемого объекта в размерном виде.
a1=F1; a2=F2 ; a3=F3.
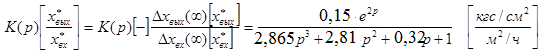
Часть 2. Дана кривая разгона исследуемого объекта. Определим вид передаточной функции.
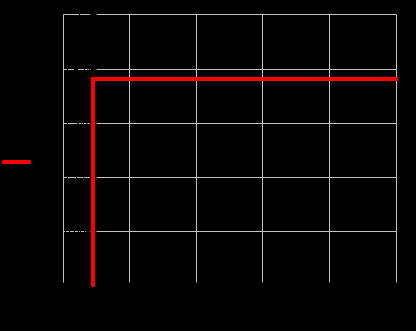
Рис. 5.1. График изменения уровня
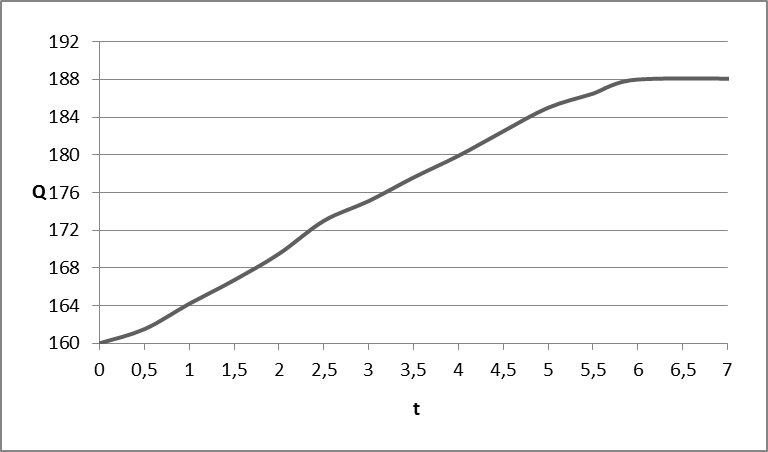
Рис. 5.2. График изменения расхода
Разбиваем ось времени на отрезки с интервалом t = 0.5 исходя из условия того, что на протяжении всего графика функция Qвых в пределах 2t мало отличается от прямой.
Заполним таблицу 5.1. Для этого находим значения Qвыхв конце каждого интервала t.
Qвых (∞)= 0.5
Таблица 5.2
По виду графика определим тип передаточной функции в безразмерном виде:
Задача состоит в том, чтобы определить неизвестные коэффициенты полиномов числителя и знаменателя. Определим площади F1 , F2 , F3для нахождения неизвестных коэффициентов.
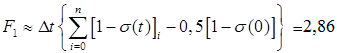
Таким образом, функция приведена к безразмерному виду.
Перестраиваем функцию
в другом масштабе времени (за независимую переменную примем переменную )
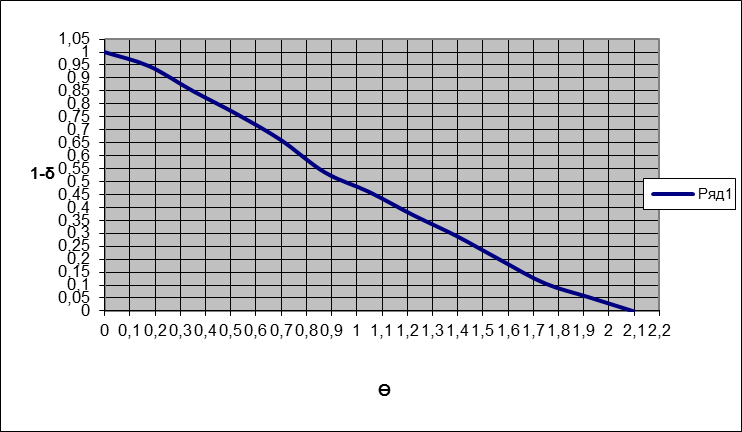
Заполняем таблицу 5.2 и находим коэффициент F2, F3.
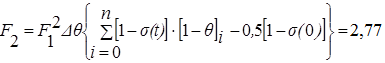
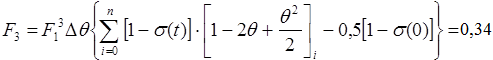
К
оэффициентом F3 можем пренебречь. Тогда передаточная функция будет иметь вид:
Записываем окончательное выражение исследуемого объекта в размерном виде.
a1=F1; a2=F2 ; a3=F3.
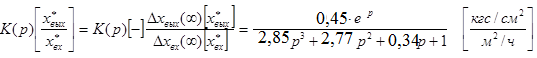
5.4. Расчет комбинированной САР и исследование влияния компенсатора на качество процесса регулирования
Даны передаточные функции объекта по каналам возмущения и регулирования и передаточная функция регулятора:
Необходимо выбрать структуру компенсатора WK(p) и рассчитать параметры компенсатора из условия инвариантности при w=0 и w=wp.
Расчет настроек регулятора и определение рабочей частоты проведем методом РАФХ для m=0.221
Нвых (∞)= 0.5
Таблица 5.1| Hвых | δ | 1-δ | Ө |
| 0 | 0 | 1 | 0 |
| 0,04 | 0,059701 | 0,940299 | 0,175439 |
| 0,1 | 0,149254 | 0,850746 | 0,350877 |
| 0,17 | 0,253731 | 0,746269 | 0,526316 |
| 0,24 | 0,358209 | 0,641791 | 0,701754 |
| 0,31 | 0,462687 | 0,537313 | 0,877193 |
| 0,38 | 0,567164 | 0,432836 | 1,052632 |
| 0,4 | 0,597015 | 0,402985 | 1,22807 |
| 0,49 | 0,731343 | 0,268657 | 1,403509 |
| 0,54 | 0,80597 | 0,19403 | 1,578947 |
| 0,59 | 0,880597 | 0,119403 | 1,754386 |
| 0,63 | 0,940299 | 0,059701 | 1,929825 |
| 0,67 | 1 | 0 | 2,105263 |
| | | | |
| | | 6,19403 | |
По виду графика определим тип передаточной функции в безразмерном виде:
Задача состоит в том, чтобы определить неизвестные коэффициенты полиномов числителя и знаменателя. Определим площади F1 , F2 , F3для нахождения неизвестных коэффициентов.
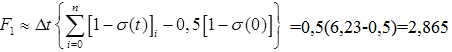
Таким образом, функция приведена к безразмерному виду.
Перестраиваем функцию
в другом масштабе времени (за незави-симую переменную примем переменную ).
Заполняем таблицу 5.2 и находим коэффициент F2, F3.| 1-δ | Ө | Ө | 1-δ(t) | 1-Ө | 1-δ(t)-1-Ө | 1-2*Ө+Ө^2/2 | (1-σ)*(1-2*Ө+Ө^2/2) |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0,940299 | 0,175439 | 0,1 | 0,975 | 0,9 | 0,8775 | 0,805 | 0,784875 |
| 0,850746 | 0,350877 | 0,2 | 0,93 | 0,8 | 0,744 | 0,62 | 0,5766 |
| 0,746269 | 0,526316 | 0,3 | 0,88 | 0,7 | 0,616 | 0,445 | 0,3916 |
| 0,641791 | 0,701754 | 0,4 | 0,822 | 0,6 | 0,4932 | 0,28 | 0,23016 |
| 0,537313 | 0,877193 | 0,5 | 0,761 | 0,5 | 0,3805 | 0,125 | 0,095125 |
| 0,432836 | 1,052632 | 0,6 | 0,702 | 0,4 | 0,2808 | -0,02 | -0,01404 |
| 0,402985 | 1,22807 | 0,7 | 0,642 | 0,3 | 0,1926 | -0,155 | -0,09951 |
| 0,268657 | 1,403509 | 0,8 | 0,585 | 0,2 | 0,117 | -0,28 | -0,1638 |
| 0,19403 | 1,578947 | 0,9 | 0,523 | 0,1 | 0,0523 | -0,395 | -0,206585 |
| 0,119403 | 1,754386 | 1 | 0,46 | 0 | 0 | -0,5 | -0,23 |
| 0,059701 | 1,929825 | 1,1 | 0,42 | -0,1 | -0,042 | -0,595 | -0,2499 |
| 0 | 2,105263 | 1,2 | 0,416 | -0,2 | -0,0832 | -0,68 | -0,28288 |
| | | 1,3 | 0,345 | -0,3 | -0,1035 | -0,755 | -0,260475 |
| | | 1,4 | 0,265 | -0,4 | -0,106 | -0,82 | -0,2173 |
| | | 1,5 | 0,225 | -0,5 | -0,1125 | -0,875 | -0,196875 |
| | | 1,6 | 0,182 | -0,6 | -0,1092 | -0,92 | -0,16744 |
| | | 1,7 | 0,141 | -0,7 | -0,0987 | -0,955 | -0,134655 |
| | | 1,8 | 0,11 | -0,8 | -0,088 | -0,98 | -0,1078 |
| | | 1,9 | 0,065 | -0,9 | -0,0585 | -0,995 | -0,064675 |
| | | 2 | 0,032 | -1 | -0,032 | -1 | -0,032 |
| | | 2,1 | 0 | -1,1 | 0 | -0,995 | 0 |
| | | | 10,481 | | 3,9203 | | 0,650425 |
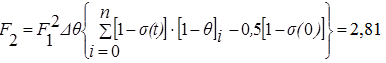
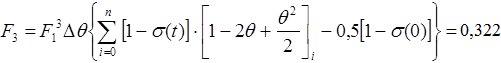
К
оэффициентом F3 можем пренебречь. Тогда передаточная функция будет иметь вид:
Записываем окончательное выражение исследуемого объекта в размерном виде.
a1=F1; a2=F2 ; a3=F3.
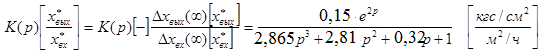
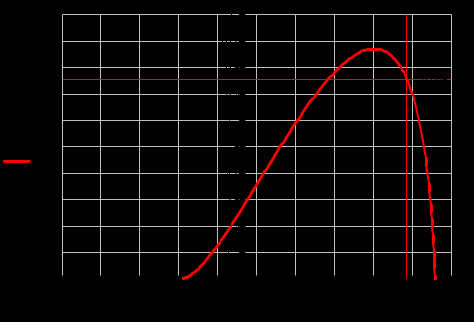
Часть 2. Дана кривая разгона исследуемого объекта. Определим вид передаточной функции.
Рис. 5.1. График изменения уровня
Рис. 5.2. График изменения расхода
Разбиваем ось времени на отрезки с интервалом t = 0.5 исходя из условия того, что на протяжении всего графика функция Qвых в пределах 2t мало отличается от прямой.
Заполним таблицу 5.1. Для этого находим значения Qвыхв конце каждого интервала t.
Qвых (∞)= 0.5
Таблица 5.2| Qвых | t | δ | 1-δ | Ө |
| 0 | 0 | 0 | 1 | 0 |
| 1,5 | 0,5 | 0,053571 | 0,9464286 | 0,17452007 |
| 4,2 | 1 | 0,15 | 0,85 | 0,34904014 |
| 6,7 | 1,5 | 0,239286 | 0,7607143 | 0,523560209 |
| 9,5 | 2 | 0,339286 | 0,6607143 | 0,698080279 |
| 13 | 2,5 | 0,464286 | 0,5357143 | 0,872600349 |
| 15,1 | 3 | 0,539286 | 0,4607143 | 1,047120419 |
| 17,6 | 3,5 | 0,628571 | 0,3714286 | 1,221640489 |
| 19,9 | 4 | 0,710714 | 0,2892857 | 1,396160558 |
| 22,5 | 4,5 | 0,803571 | 0,1964286 | 1,570680628 |
| 25 | 5 | 0,892857 | 0,1071429 | 1,745200698 |
| 26,5 | 5,5 | 0,946429 | 0,0535714 | 1,919720768 |
| 28 | 6 | 1 | 0 | 2,094240838 |
| | | | 6,2321429 | |
По виду графика определим тип передаточной функции в безразмерном виде:
Задача состоит в том, чтобы определить неизвестные коэффициенты полиномов числителя и знаменателя. Определим площади F1 , F2 , F3для нахождения неизвестных коэффициентов.
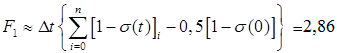
Таким образом, функция приведена к безразмерному виду.
Перестраиваем функцию
в другом масштабе времени (за независимую переменную примем переменную ) Заполняем таблицу 5.2 и находим коэффициент F2, F3.
| Ө | (1-σ) | 1-Ө | (1-σ)*(1-Ө) | 1-2*Ө+Ө^2/2 | (1-σ)*(1-2*Ө+Ө^2/2) |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 0,1 | 0,97 | 0,9 | 0,873 | 0,805 | 0,78085 |
| 0,2 | 0,93 | 0,8 | 0,744 | 0,62 | 0,5766 |
| 0,3 | 0,87 | 0,7 | 0,609 | 0,445 | 0,38715 |
| 0,4 | 0.825 | 0,6 | 0,495 | 0,28 | 0,231 |
| 0,5 | 0,775 | 0,5 | 0,3875 | 0,125 | 0,096875 |
| 0,6 | 0,725 | 0,4 | 0,29 | -0,02 | -0,0145 |
| 0,7 | 0,66 | 0,3 | 0,198 | -0,155 | -0,1023 |
| 0,8 | 0,59 | 0,2 | 0,118 | -0,28 | -0,1652 |
| 0,9 | 0,57 | 0,1 | 0,057 | -0,395 | -0,22515 |
| 1 | 0,48 | 0 | 0 | -0,5 | -0,24 |
| 1,1 | 0,44 | -0,1 | -0,044 | -0,595 | -0,2618 |
| 1,2 | 0,38 | -0,2 | -0,076 | -0,68 | -0,2584 |
| 1,3 | 0,33 | -0,3 | -0,099 | -0,755 | -0,24915 |
| 1,4 | 0,288 | -0,4 | -0,1152 | -0,82 | -0,23616 |
| 1,5 | 0,24 | -0,5 | -0,12 | -0,875 | -0,21 |
| 1,6 | 0,18 | -0,6 | -0,108 | -0,92 | -0,1656 |
| 1,7 | 0,14 | -0,7 | -0,098 | -0,955 | -0,1337 |
| 1,8 | 0,08 | -0,8 | -0,064 | -0,98 | -0,0784 |
| 1,9 | 0,06 | -0,9 | -0,054 | -0,995 | -0,0597 |
| 2 | 0,035 | -1 | -0,035 | -1 | -0,035 |
| 2,1 | 0 | -1,1 | 0 | -0,995 | 0 |
| | | | 3,9583 | | 0,637415 |
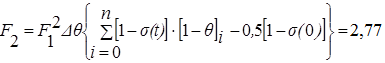
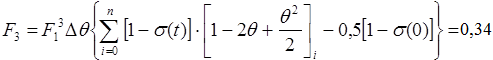
К
оэффициентом F3 можем пренебречь. Тогда передаточная функция будет иметь вид:
Записываем окончательное выражение исследуемого объекта в размерном виде.
a1=F1; a2=F2 ; a3=F3.
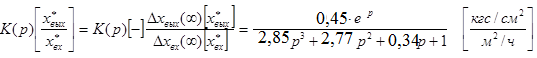
5.4. Расчет комбинированной САР и исследование влияния компенсатора на качество процесса регулированияДаны передаточные функции объекта по каналам возмущения и регулирования и передаточная функция регулятора:
Необходимо выбрать структуру компенсатора WK(p) и рассчитать параметры компенсатора из условия инвариантности при w=0 и w=wp.
-
Рассчитать настроечные параметры регулятора и рабочую частоту wp.
Расчет настроек регулятора и определение рабочей частоты проведем методом РАФХ для m=0.221