Файл: Направление подготовки.docx

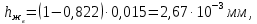
Рассчитаем высоту слоя жидкости для верхней и нижней части колонны, используя уравнение (51):Высота светлого слоя жидкости определяется по соотношению:

(52)

где – высота сливной планки; 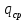– средняя линейная плотность орошения определяемая следующим уравнением:

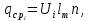(53)

где – плотность орошения (приведённая скорость жидкости), отнесённая к единице рабочей площади тарелки, м³/(м²×с); 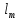–средняя длина пути жидкости на тарелке, м.Среднюю длину пути жидкости определяется выражением:

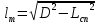	(54)
Рассчитаем среднюю длину пути жидкости, используя уравнение (54):

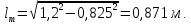
Плотность орошения рассчитываем по формуле:

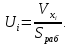(55)

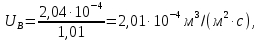
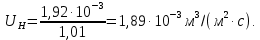
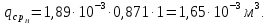
Рассчитаем плотность орошения в верхней и нижней части колонны по уравнению (55):Средняя линейная плотность орошения:В результате посчитаем высоту светлого слоя жидкости, используя уравнение (52):

---

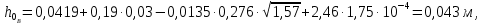
Высота газожидкостного (барботажного) слоя определяется по формуле:

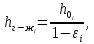(56)

где 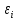– газосодержание барботажного слоя.Величина 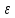определяется по соотношению:

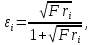(57)

где – критерий Фруда определяемый:

(58)

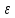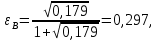
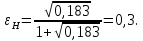
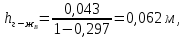
Рассчитаем критерий Фруда по уравнению (58):Рассчитаем величину , используя уравнение (57):Рассчитаем высоту газожидкостного слоя, используя уравнение (56):Брызгоунос для колпачковых тарелок рассчитывается по формуле:

(59)

где – брызгоунос; 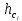– высота сепарационного пространства, м; 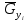– массовый расход газа (пара), кг/с; – рабочая площадь тарелки, м²;

---

– динамический коэффициент вязкости жидкости, мПа с; 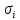– поверхностное натяжение, мН/м; – скорость газа (пара), отнесённая к единице площади поперечного сечения колонны, м/с.

Высоту сепарационного пространства определяем по формуле:

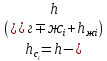(60)

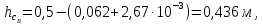
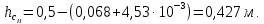
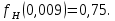
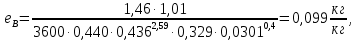
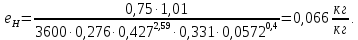
Рассчитаем высоту сепарационного пространства:Значение функции равны:Рассчитываем брызгоунос:Чтобы убедиться в том, что колонна работает без захлёбывания, необходимо проверить скорость жидкости в переливном устройстве. Максимально допустимую скорость жидкости в переливном устройстве выбираем по наименьшей величине, рассчитанной по трём соотношениям:

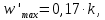	(61)
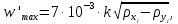	(62)
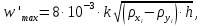	(63)

где – коэффициент, значения которого зависят от свойств разделяемой смеси и равен 0,9.Рассчитаем максимально допустимую скорость жидкости в переливном устройстве по формулам (61), (62) и (63):

---

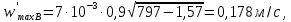
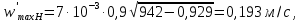
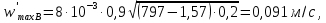
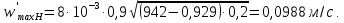
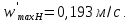
Окончательно выбираем максимальную скорость: Фактическую скорость жидкости в переливном устройстве определяем по соотношению:

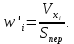(64)

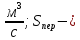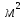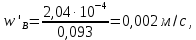
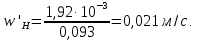
где объемный расход жидкости, площадь сечения перелива, .Рассчитаем фактическую скорость по уравнению (64):Условие выполняется

4.2.3 Расчёт сопротивления тарелки

Гидравлическое сопротивление тарелки (всех типов) можно определить, как сумму сопротивлений:

(65)

где – сопротивление сухой тарелки, Па;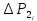 – сопротивление, обусловленное силами поверхностного натяжения, Па; 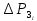– сопротивление газожидкостного (барботажного) слоя, Па.Сопротивление сухой тарелки определяется уравнением:

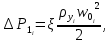(66)

где – коэффициент сопротивления , 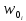- скорость пара в паровых патрубках, м/с.

((67)

---

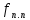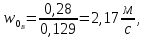
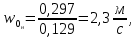
где - сечение паровых патрубков, м^2.Сопротивление 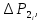обусловленное силами поверхностного натяжения, возникает при выходе газа (пара) из отверстий (щелей) в слой жидкости. Так как его значение пренебрежимо мало, в проектировочных расчётах его не учитываютСопротивление газожидкостного (барботажного) слоя принимают равным статическому давлению слоя:

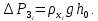(68)

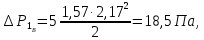
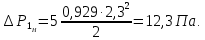
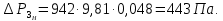
Рассчитываем сопротивление сухой тарелки, используя уравнение (66):Сопротивление газожидкостного слоя определяем по уравнению (68): Гидравлическое сопротивление тарелки рассчитываем по уравнению (65):

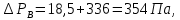
4.2.4 Расчёт высоты колонны

Коэффициент массоотдачи можно рассчитать по следующим соотношениям:

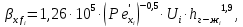	(68)
	(69)

где – диффузионный критерий Пекле.Диффузионный критерий Пекло рассчитывается по следующим формулам:

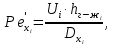	(70)
	(71)

Рассчитаем диффузионные критерии Пекле для верха и низа колонны обеих фаз по уравнениям (70) и (71):

---