Добавлен: 23.11.2023
Просмотров: 140
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «Национальный исследовательский ядерный университет «МИФИ»
Снежинский физико-технический институт –
филиал федерального государственного автономного образовательного учреждения высшего
профессионального образования «Национальный исследовательский ядерный университет «МИФИ»
(СФТИ НИЯУ МИФИ)
Кафедра АИВС
КУРСОВАЯ РАБОТА
ПО КУРСУ: «Системы цифровой обработки сигналов»
НА ТЕМУ: «Разработка БИХ-фильтра на основе фильтра прототипа»
Группа: ПАС-49Д
Студент: Крушная М.М. ____________________
Преподаватель: Пыхов В.В._________________
г.Снежинск
2023
Вариант №4
Тема: Разработка БИХ-фильтра на основе фильтра прототипа.
Цель: Разработать БИХ-фильтр на основе фильтра прототипа в соответствии с заданием.
Задание: В качестве фильтра прототипа использовать фильтр Баттерворта. Порядок фильтра определить исходя из требований к проектированию: частота среза (Fc), граничная частота полосы подавления (Fs), неравномерность в полосе пропускания (Ap), ослабление в полосе подавления (As). Для синтеза БИХ-фильтра использовать билинейное z-преобразование. Фильтр реализовать в целочисленной знаковой арифметике, представленной 8, 16, 32, 64 бит (необходимо выбрать минимальную разрядность, соответствующую требованиям спецификации фильтра). Проверить устойчивость фильтра при реализации в целочисленной знаковой арифметике. Реализовать фильтр в канонической форме, рассчитать отклик фильтра на тестовый сигнал.
Дано:
| № | Тип фильтра | Граничная частота | Частота среза | Затухание в полосе подавления | Частота дискретизации | Неравномерность в полосе пропускания |
| 4 | НЧ | 800 Гц | 180 Гц | 50 дБ | 2500 Гц | 3 дБ |
Содержание
| Введение | 4 |
| 1 Выбор и расчет фильтра прототипа | 5 |
| 2 Синтез цифрового фильтра | 7 |
| 3 Переход в знаковую целочисленную арифметику | 9 |
| 4 Анализ соответствия цифрового фильтра заданной спецификации | 11 |
| 5 Анализ устойчивости цифрового фильтра | 13 |
| 6 Математическая модель фильтрации сигнала | 14 |
| Заключение | 18 |
| Литература | 19 |
| Приложение 1. Таблица значений отклика тестового сигнала | 20 |
Введение
Целью данной курсовой работы является разработка БИХ-фильтра на основе фильтра прототипа.
В качестве фильтра прототипа надо использовать фильтр Баттерворта. Порядок фильтра определить исходя из требований к проектированию. Для синтеза БИХ-фильтра необходимо использовать билинейное z-преобразование. Фильтр требуется реализовать в целочисленной знаковой арифметике, представленной 8, 16, 32, 64 бит. Затем проверить устойчивость фильтра при реализации в целочисленной знаковой арифметике и реализовать фильтр в канонической форме, рассчитать отклик фильтра на тестовый сигнал в программе Mathcad.
Курсовая работа состоит из 6 разделов, 1 приложения и составляет 32 страницы.
1 Выбор и расчет фильтра прототипа
В качестве фильтра прототипа, согласно заданию, был выбран фильтр Баттерворта. На основе спецификации находим деформированные частоты:
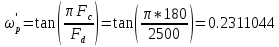
(1.1)
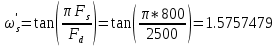
(1.2)
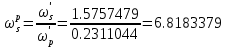
(1.3)
где
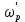– деформированная граничная частота полосы пропускания,
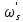– деформированная граничная частота полосы подавления,
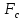– частота среза,
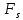– граничная частота полосы подавления,
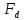– частота дискретизации.Порядок фильтра определяется соотношением (1.4), где
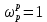для ФНЧ-прототипа: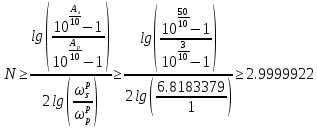
(1.4)
где
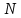– порядок фильтра,
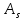– ослабление в полосе подавления,
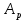– неравномерность в полосе пропускания.П
(1.5)
усть
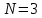, тогда передаточная функция фильтра-прототипа будет иметь вид: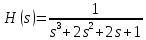
где
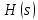– передаточная функция,s – комплексная переменная.
2 Синтез цифрового фильтра
Ч
(2.1)
астотно-масштабированная передаточная функция на s-плоскости
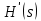записывается так: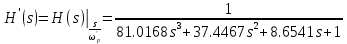
(2.2)
После применения билинейное z-преобразование получается следующая передаточная фукнция
:
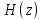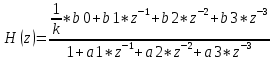
где
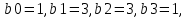
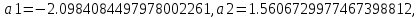
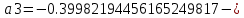коэффициенты фильтра,
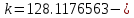коэффициент общего делителя.В программе Mathcad были получены АЧХ фильтра с идеальной передаточной функцией и АЧХ фильтра после билинейного z-преобразования. График сравнения АЧХ представлен на рисунке 1. Штрих-пунктирной линией обозначена АЧХ фильтра с идеальной передаточной функцией, сплошной линией обозначена АЧХ фильтра после билинейного z-преобразования.
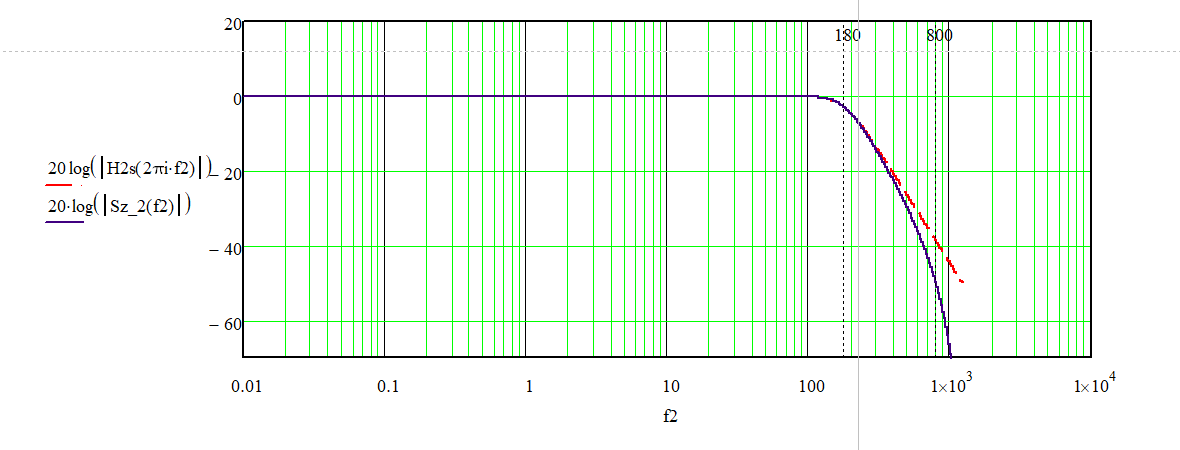
Рисунок 1 – Сравнение АЧХ
В программе Mathcad были расчитаны значения передаточных функций для частоты среза и граничной частоты полосы подавления.
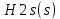
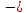идеальная передаточная функция,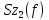
(2.3)
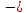передаточная функция после билинейного z-преобразования.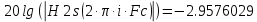
(2.4)
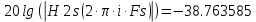
(2.5)
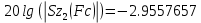
(2.6)
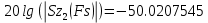
После билинейного z-преобразования, согласно расчетам, неравномерность в полосе пропускания лежит в пределах спецификации, а ослабление в полосе подавления стало меньше требуемого значения. Следовательно, для получения более точных характеристик можно использовать квантование коэффициентов.
3 Переход в знаковую целочисленную арифметику
Для реализации фильтра в целочисленной арифметике был выбран восьмибитный базис. Символами 
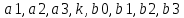обозначены неквантованные коэффициенты. Символами 
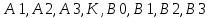обозначены квантованные коэффициенты.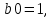
,
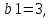
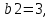
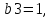
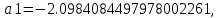
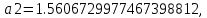
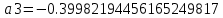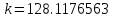.Коэффициенты
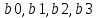
останутся неизменными, так как являются целочисленными и не подвергнутся квантованию.
Поскольку есть отрицательные коэффициенты, то 1 бит выделяется для хранения бита знака, 1 бит для целой и 6 бит – для дробной части коэффициента. Коэффициент k принимает ближайшее целочисленное число в двоичной системе равное 128. Таким образом, после квантования до 8 бит коэффициенты приобретают такие значения:
,
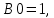
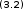
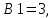
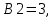
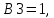
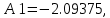
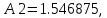
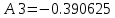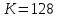.После квантования коэффициентов получается следующая передаточная фукнция
:
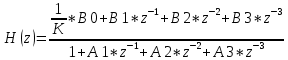
(3.3)
где коэффициенты принимают значения соответствующие системе (3.2).
4 Анализ соответствия цифрового фильтра заданной спецификации
В программе Mathcad были получены АЧХ фильтра с идеальной передаточной функцией и АЧХ фильтра после квантования коэффициентов. График сравнения АЧХ представлен на рисунке 2. Штрих-пунктирной линией обозначена АЧХ фильтра с идеальной передаточной функцией, сплошной линией обозначена АЧХ фильтра после квантования коэффициентов.
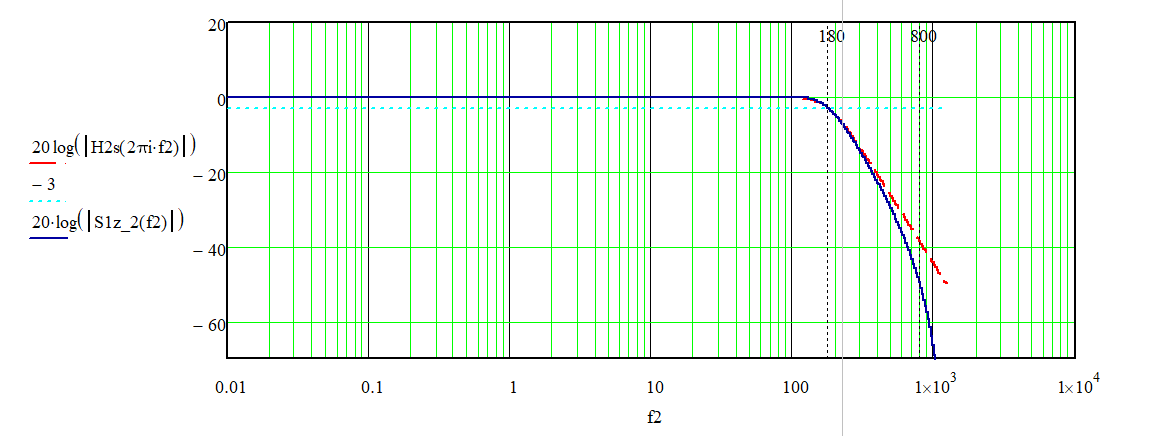
Рисунок 2 – Сравнение АЧХ после квантования коэффициентов
В программе Mathcad были расчитаны значения передаточных функций для частоты среза и граничной частоты полосы подавления.
идеальная передаточная функция,