Добавлен: 23.11.2023
Просмотров: 144
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(4.1)
передаточная функция после квантования коэффициентов.
(4.2)
(4.3)
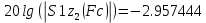
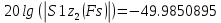
(4.4)
После билинейного z-преобразования, согласно расчетам, неравномерность в полосе пропускания и ослабление в полосе подавления соответствуют требуемой спецификации. Следовательно, можно не увеличивать базис.
5 Анализ устойчивости цифрового фильтра
Согласно критерию оценки устойчивости цифровой фильтр устойчив, если полюсы системной функции располагаются внутри круга единичного радиуса с центром в начале координат
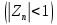.П
(5.1)
олюсы системной функции получившегося фильтра находятся через соотношение:
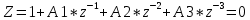
С
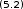огласно соотношению (5.1) полюсы равны: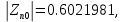 
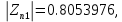
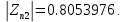
Так как все полюсы меньше единицы, следовательно получившийся фильтр устойчив.
6 Математическая модель фильтрации сигнала
Полученный фильтр был реализован в каноническом виде, согласно схеме, представленной на рисунке 3.
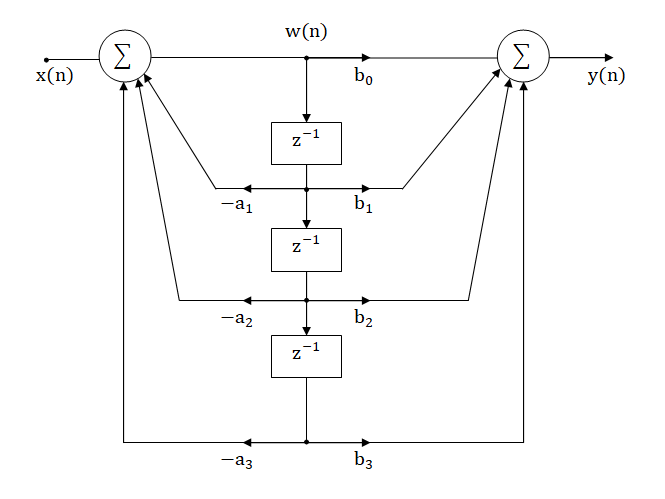Рисунок 3 – каноническое звено третьего порядкаВ среде Mathcad был сформирован прямоугольный сигнал, представленный на рисунке 4, и расчитан отклик фильтра на этот сигнал.
Отклик фильтра на тестовый сигнал представлен на рисунке 5. Значения отсчетов содоржатся в приложении 1.
Спектры входного и выходного сигнала
, а также разница спектров входного и выходного сигналов представлены на рисунках 6, 7 и 8 соответственно.
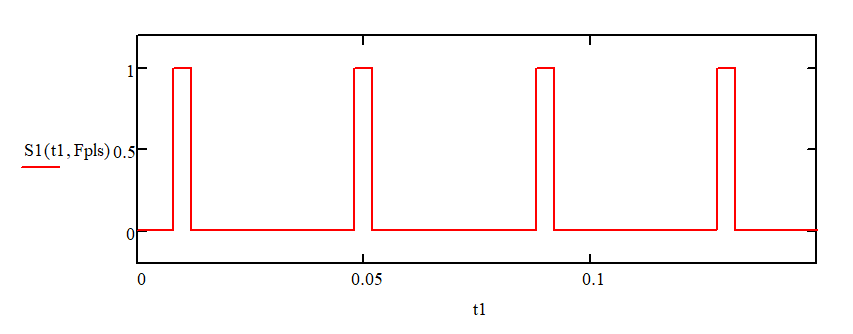Рисунок 4 – Входной сигнал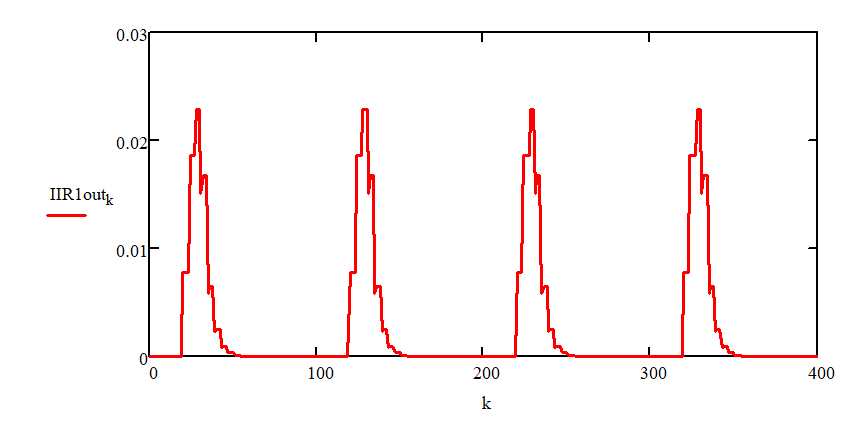
Рисунок 5 – Выходной сигнал
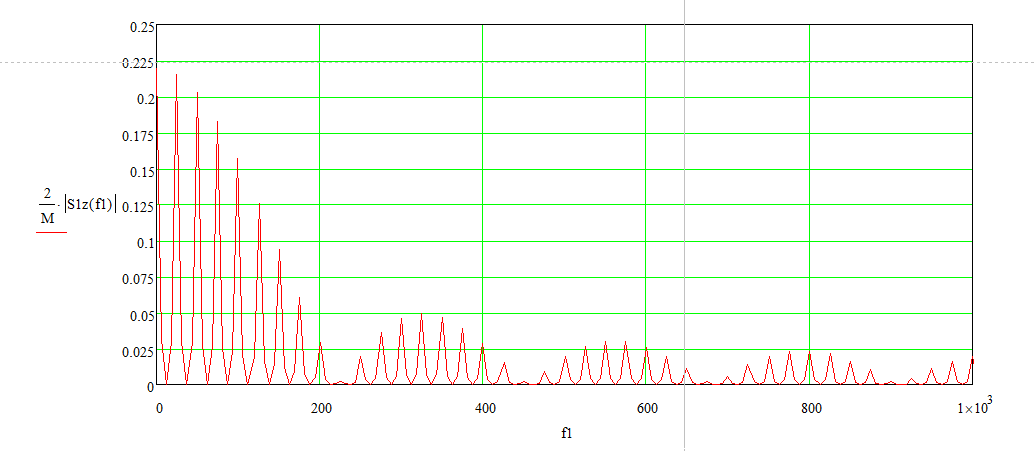
Рисунок 6 – Спектр входного сигнала
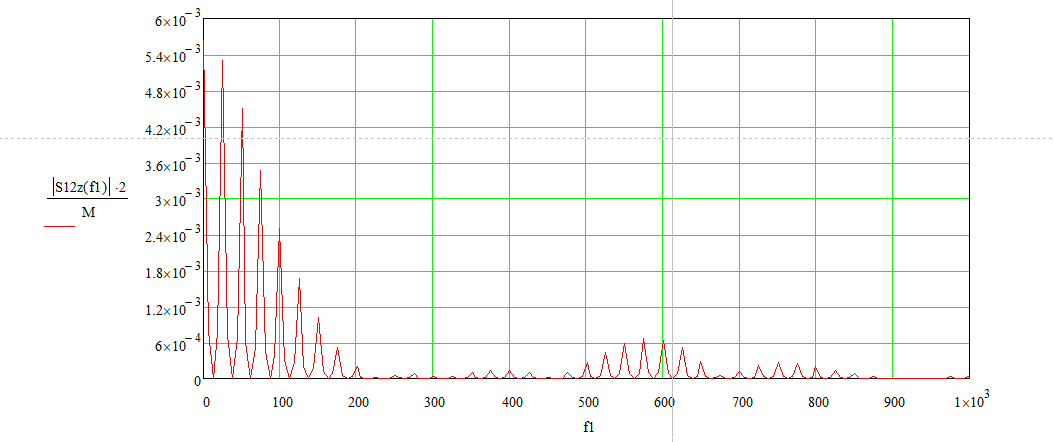
Рисунок 7 – Спектр выходного сигнала
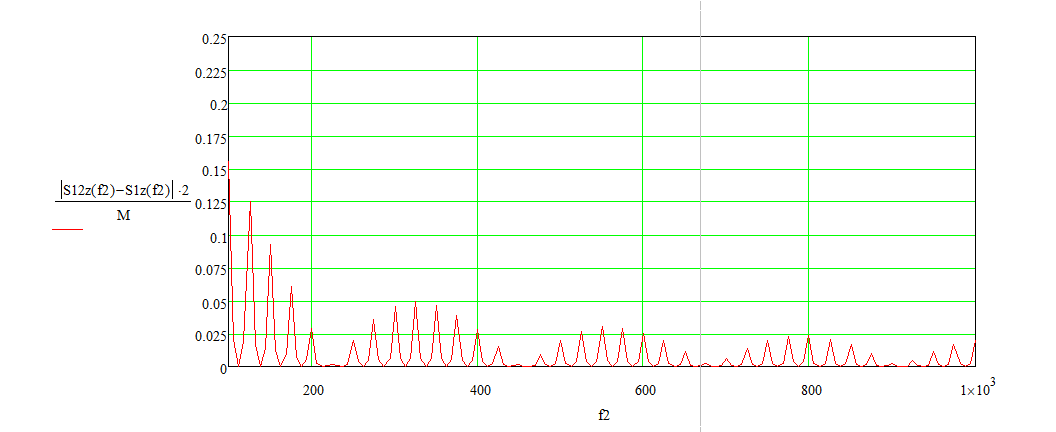
Рисунок 8 – Разница спектров выходного и входного сигналов
Заключение
В ходе курсовой работы был разработан БИХ-фильтр на основе фильтра прототипа Баттерворта. Порядок фильтра был определен исходя из требований к проектированию. После синтеза фильтра был произведен переход в знаковую целочисленную арифметику. Квантованный фильтр в последствии был проверен на устойчивость и проанализирован на соответсвие заданной спецификации. Итогом курсовой работы стал расчет отклика фильтра на тестовый сигнал.
Литература
-
Межгосударственный стандарт ГОСТ 2.105-95 "Единая система конструкторской документации. Общие требования к текстовым документам"; -
Айфичер, Эммануил С., Джервис, Барри У. Цифровая обработка сигналов: практический подход, 2-е издание. : Пер. с англ. – М.: Издательский дом “Вильямс”, 2004. – 992 с. : ил. – Парал. тит. англ. -
Коберниченко, В. Г. Расчет и проектирование цифровых фильтров : [учеб.-метод. пособие] / В. Г. Коберниченко. – Екатеринбург : Изд-во Урал. ун-та, 2013 – 64 с.
Приложение 1. Таблица значений отклика тестового сигнала
| y(0) | 0 | y(26) | 0,018677 | y(52) | 0,000152 |
| y(1) | 0 | y(27) | 0,018677 | y(53) | 0,000152 |
| y(2) | 0 | y(28) | 0,022921 | y(54) | 0,000152 |
| y(3) | 0 | y(29) | 0,022921 | y(55) | 5,37E-05 |
| y(4) | 0 | y(30) | 0,022921 | y(56) | 5,96E-05 |
| y(5) | 0 | y(31) | 0,015108 | y(57) | 5,96E-05 |
| y(6) | 0 | y(32) | 0,016766 | y(58) | 5,96E-05 |
| y(7) | 0 | y(33) | 0,016766 | y(59) | 2,1E-05 |
| y(8) | 0 | y(34) | 0,016766 | y(60) | 2,33E-05 |
| y(9) | 0 | y(35) | 0,005902 | y(61) | 2,33E-05 |
| y(10) | 0 | y(36) | 0,006549 | y(62) | 2,33E-05 |
| y(11) | 0 | y(37) | 0,006549 | y(63) | 8,19E-06 |
| y(12) | 0 | y(38) | 0,006549 | y(64) | 9,09E-06 |
| y(13) | 0 | y(39) | 0,002305 | y(65) | 9,09E-06 |
| y(14) | 0 | y(40) | 0,002558 | y(66) | 9,09E-06 |
| y(15) | 0 | y(41) | 0,002558 | y(67) | 3,2E-06 |
| y(16) | 0 | y(42) | 0,002558 | y(68) | 3,55E-06 |
| y(17) | 0 | y(43) | 0,000901 | y(69) | 3,55E-06 |
| y(18) | 0 | y(44) | 0,000999 | y(70) | 3,55E-06 |
| y(19) | 0 | y(45) | 0,000999 | y(71) | 1,25E-06 |
| y(20) | 0,007813 | y(46) | 0,000999 | y(72) | 1,39E-06 |
| y(21) | 0,007813 | y(47) | 0,000352 | y(73) | 1,39E-06 |
| y(22) | 0,007813 | y(48) | 0,00039 | y(74) | 1,39E-06 |
| y(23) | 0,007813 | y(49) | 0,00039 | y(75) | 4,88E-07 |
| y(24) | 0,018677 | y(50) | 0,00039 | y(76) | 5,42E-07 |
| y(25) | 0,018677 | y(51) | 0,000137 | y(77) | 5,42E-07 |
Продолжение приложения 1
| y(78) | 5,42E-07 | y(105) | 7,52E-10 | y(132) | 0,016766 |
| y(79) | 1,91E-07 | y(106) | 7,52E-10 | y(133) | 0,016766 |
| y(80) | 2,12E-07 | y(107) | 2,65E-10 | y(134) | 0,016766 |
| y(81) | 2,12E-07 | y(108) | 2,94E-10 | y(135) | 0,005902 |
| y(82) | 2,12E-07 | y(109) | 2,94E-10 | y(136) | 0,006549 |
| y(83) | 7,45E-08 | y(110) | 2,94E-10 | y(137) | 0,006549 |
| y(84) | 8,27E-08 | y(111) | 1,03E-10 | y(138) | 0,006549 |
| y(85) | 8,27E-08 | y(112) | 1,15E-10 | y(139) | 0,002305 |
| y(86) | 8,27E-08 | y(113) | 1,15E-10 | y(140) | 0,002558 |
| y(87) | 2,91E-08 | y(114) | 1,15E-10 | y(141) | 0,002558 |
| y(88) | 3,23E-08 | y(115) | 4,04E-11 | y(142) | 0,002558 |
| y(89) | 3,23E-08 | y(116) | 4,48E-11 | y(143) | 0,000901 |
| y(90) | 3,23E-08 | y(117) | 4,48E-11 | y(144) | 0,000999 |
| y(91) | 1,14E-08 | y(118) | 4,48E-11 | y(145) | 0,000999 |
| y(92) | 1,26E-08 | y(119) | 1,58E-11 | y(146) | 0,000999 |
| y(93) | 1,26E-08 | y(120) | 0,007813 | y(147) | 0,000352 |
| y(94) | 1,26E-08 | y(121) | 0,007813 | y(148) | 0,00039 |
| y(95) | 4,44E-09 | y(122) | 0,007813 | y(149) | 0,00039 |
| y(96) | 4,93E-09 | y(123) | 0,007813 | y(150) | 0,00039 |
| y(97) | 4,93E-09 | y(124) | 0,018677 | y(151) | 0,000137 |
| y(98) | 4,93E-09 | y(125) | 0,018677 | y(152) | 0,000152 |
| y(99) | 1,73E-09 | y(126) | 0,018677 | y(153) | 0,000152 |
| y(100) | 1,92E-09 | y(127) | 0,018677 | y(154) | 0,000152 |
| y(101) | 1,92E-09 | y(128) | 0,022921 | y(155) | 5,37E-05 |
| y(102) | 1,92E-09 | y(129) | 0,022921 | y(156) | 5,96E-05 |
| y(103) | 6,77E-10 | y(130) | 0,022921 | y(157) | 5,96E-05 |
| y(104) | 7,52E-10 | y(131) | 0,015108 | y(158) | 5,96E-05 |
Продолжение приложения 1