– в ходе представления проекта давать оценку его результатам;

– самостоятельно осознавать причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха;

– уметь оценить степень успешности своей индивидуальной образовательной деятельности;

Средством формирования регулятивных УУД служат технология системно- деятельностного подхода на этапе изучения нового материала и технология оценивания образовательных достижений (учебных успехов).

Познавательные:

– анализировать, сравнивать, классифицировать и обобщать факты и явления;

– осуществлять сравнение, сериацию и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций; строить классификацию путём дихотомического деления (на основе отрицания);

– строить логически обоснованное рассуждение, включающее установление причинно-следственных связей;

– создавать математические модели;

– составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.);

– вычитывать все уровни текстовой информации.

– уметь определять возможные источники необходимых сведений, производить поиск информации, анализировать и оценивать её достоверность.

– понимая позицию другого человека, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории. Для этого самостоятельно использовать различные виды чтения (изучающее, просмотровое, ознакомительное, поисковое), приёмы слушания.

– уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей. Уметь выбирать адекватные задаче инструментальные программно-аппаратные средства и сервисы.

Средством формирования познавательных УУД служат учебный материал и прежде всего продуктивные задания учебника.

– Использование математических знаний для решения различных математических задач и оценки полученных результатов.

– Совокупность умений по использованию доказательной математической речи.

– Совокупность умений по работе с информацией, в том числе и с различными математическими текстами.

---

– Умения использовать математические средства для изучения и описания реальных процессов и явлений.

– Независимость и критичность мышления.

– Воля и настойчивость в достижении цели.

Коммуникативные:

– самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.);

– отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами;

– в дискуссии уметь выдвинуть контраргументы;

– учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;

– понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;

Средством формирования коммуникативных УУД служат технология проблемного обучения, организация работы в малых группах, также использование на уроках технологии личностно- ориентированного и системно- деятельностного обучения.

Личностные достижения учащихся

• 
  использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
  

моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры

описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

интерпретации графиков реальных зависимостей между величинами.

• 
  формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов
  
• 
  формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики
  
• 
  формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности
  
• 
  умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры
  
• 
  критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта
  
• 
  креативность мышления, инициативу, находчивость, активность при решении алгебраических задач
  
• 
  умение контролировать процесс и результат учебной математической деятельности
  
• 
  способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
  

---

Содержание учебного предмета

1.Рациональные дроби

Рациональная дробь. Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений. Функция у = 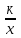и её график.

Цель: выработать умение выполнять тождественные преобразования рациональных выражений.

Так как действия с рациональными дробями существенным образом опираются на действия с многочленами, то в начале темы необходимо повторить с обучающимися преобразования целых выражений.

Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумму, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразованиях дробных выражений. Поэтому им следует уделить особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. Задания на все действия с дробями не должны быть излишне громоздкими и трудоемкими.

При нахождении значений дробей даются задания на вычисления с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел.

Изучение темы завершается рассмотрением свойств графика функции у = .

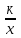УУД:

Коммуникативные:

Слушать и слышать друг друга; представлять конкретное содержание и сообщать его в письменной и устной форме.

Регулятивные:

Принимать познавательную цель, сохранять её при выполнении учебных действий, регулировать весь процесс их выполнения и чётко выполнять требования познавательной задачи.

Познавательные:

Выводить следствия из имеющихся в условии задачи данных; устанавливать причинно-следственные связи.

2.Квадратные корни

Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция у = 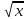, её свойства и график.

Цель:

систематизировать сведения о рациональных числах и дать представление об иррациональных чис­лах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.

---

В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные обучающимся сведения о рациональных числах. Для введе­ния понятия иррационального числа используется интуитивное представление о том, что каждый отрезок имеет длину и потому каждой точке координатной прямой соответствует некоторое число. Показывается, что существуют точки, не имеющие рациональных абсцисс.

При введении понятия корня полезно ознакомить обучающихся с нахождением корней с помощью калькулятора.

Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество 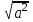= 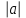, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 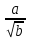, 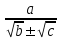. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.

Продолжается работа по развитию функциональных представлений обучающихся. Рассматриваются функция у= , её свойства и график. При изучении функции у= , показывается ее взаимосвязь с функцией у = х², где х ≥ 0.

УУД:

Коммуникативные:

Слушать и слышать друг друга; представлять конкретное содержание и сообщать его в письменной и устной форме.

Регулятивные:

Принимать познавательную цель, сохранять её при выполнении учебных действий, регулировать весь процесс их выполнения и чётко выполнять требования познавательной задачи.

Познавательные:

Выводить следствия из имеющихся в условии задачи данных; устанавливать причинно-следственные связи.

3.Квадратные уравнения

Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.

---

Цель:

выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.

В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.

Основное внимание следует уделить решению уравнений вида ах² + bх + с = 0, где а 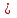0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.

Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.

Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых для решения текстовых задач.

УУД:

Коммуникативные:

Представлять конкретное содержание и сообщать его в письменной и устной форме;

Уметь (или развивать способность) с помощью вопросов добывать недостающую информацию.

Регулятивные:

Ставить учебную задачу на основе соотнесения того, что уже известно, усвоено, и того, что ещё неизвестно; самостоятельно формулировать познавательную цель и строить действия в соответствии с ней.

Познавательные:

Проводить анализ способов решения задач

4. Неравенства

Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.

Цель:

ознакомить обучающихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.

Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной Погрешности и точности приближения, относительной погрешности.

---

Смотрите также файлы

• 3 Решите три задачи, используя государственные стандарты. Сделайте заключение о качестве товара Задача 1.docx

• С 1934 года член подпольной Коммунистической партии Западной Белоруссии, созданной в деревне Цинцевичи.odt

• Особенности формирования диалога у дошкольников с легкой степенью псевдобульбарной дизартрии.docx

• Герберт Маршалл Маклюэн Риманас Елизавета Андреевна.pptx

• йымдастырылан оу ызметіні техногиялы картасы Акгершін ересек тобы Кні Білім беру саласы.docx