Файл: Отчет по лабораторной работе 3 по дисциплине Основы оптоэлектроники.docx
Добавлен: 23.11.2023
Просмотров: 62
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра электронных приборов (ЭП)
СВОЙСТВА И ПАРАМЕТРЫ ФОТОПРОВОДИМОСТИ ПОЛУПРОВОДНИКОВЫХ ФОТОРЕЗИСТОРОВ
Отчет по лабораторной работе № 3
по дисциплине «Основы оптоэлектроники»
Проверил Выполнили
Профессор каф. ЭП Студенты гр. 150
Давыдов В.Н. Бочкарева Е.Н.
«»2023 г. Ганский А.С.
«»2023 г.
Томск 2023
-
ВВЕДЕНИЕ
Цель данной работы – изучение процессов, протекающих в фоторезисторе при его освещения непрерывным излучением различной частоты и при различных значениях напряжения, приложенного к фоторезистору, а также вычисление из полученных зависимостей параметров полупроводника.
-
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
-
Основные понятия и параметры
При нарушении термодинамического равновесия, например, при освещении полупроводника, концентрации электронов и дырок в зонах (n и p) изменяются по сравнению с их равновесными значениями n0 и p0, т.к. в
зонах появляются
неравновесные носители заряда с концентрациями n n n0 и p p p0 .
Скорости генерации и рекомбинации. Установление концентраций в зонах определяется процессами генерации и рекомбинации электронов и дырок. Суммарные скорости этих процессов (количество генерируемых или рекомбинируемых частиц в единичном объеме в единицу времени) принято обозначать как g и R,соответственно (рис. 2.1).Рисунок 2.1
Это два противоположно направленных процесса, равенство которых создает термодинамическое равновесие в зонах разрешенных энергий полупроводника.
Время жизни неравновесных носителей.
Рисунок 2.2
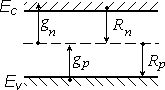
Пусть под влиянием внешнего воздействия в единице объема полупроводника
в единицу времени возникает
gn электронов проводимости и соответственно gp
дырок в валентной зоне. Скорости генерации
gn и
gp- постоянными по всему
объему полупроводника. Пусть Rnи Rp– скорости исчезновения электронов и
дырок в результате их рекомбинации. Если в полупроводнике нет электрического тока, то суммарная скорость изменения неравновесных концентраций электронов и дырок в зонах определяется скоростями их генерации и рекомбинации (рис.2.2):
n n
n g R;
t
p g R .
p p
t
Для описания кинетики неравновесных электронных процессов (развития процессов во времени) вводят понятие среднего времени жизни неравновесных
электронов в зоне проводимости n
и дырок в валентной зоне
p, которые
определяются через скорости рекомбинации электронов и дырок:
Rn n n0 ,
n
Rp
p p0
p
или иначе: 1 n
– это вероятность исчезновения одного избыточного электрона из
зоны проводимости в единицу времени в результате рекомбинации с дыркой; 1 p– вероятность рекомбинации одной дырки в единицу времени.
Пользуясь понятиями времени жизни носителей заряда, уравнения кинетики
неравновесных концентраций электронов и дырок в однородном образце, можно переписать в виде:
n gn n;
p gp p. (1)
t n t p
Стационарные концентрации неравновесных носителей заряда
(n)s
и (p)s,
устанавливающиеся после длительного воздействия внешней генерации, можно найти, если в (1) приравнять к нулю левые части. В результате этого упрощения из (1) можно найти стационарные концентрации свободных носителей заряда в зонах:
(n)s gnn; (p)s gp p. (2)
Теперь рассмотрим кинетику изменения концентраций носителей заряда. В
простейшем случае, когда nи pне зависят от nи p, интегрирование кинетических
уравнений (1) с учетом выражений (2) дает:
n(t) gn n
-
t
Cnexp ;
n
t
(3)
p(t) gp p
-
Cpexp
.
p
Здесь
Сn,
Cp– постоянные интегрирования, определяемые из начальных
условий: если в начале полупроводник находился в термодинамическом равновесии и затем в момент времени t= 0 включено внешнее воздействие (создающее
генерацию носителей заряда), то при t= 0 будем иметь n 0 . Использование
данного начального условия позволяет найти постоянные интегрирования:
t
Cn gnn (n)s;
n(t) (n)s 1 exp ;
n
t
(4)
Cp gp p (p)s;
p(t) (p)s 1 exp .
p