Файл: Отчет по лабораторной работе 3 по дисциплине Основы оптоэлектроники.docx

Скачать файл (0,42Мб)

Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 63

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Ход этих зависимостей показан на рис. 2.2 сплошной линией. Если в

^{некоторый момент времени}^{t = t}1 ^{освещение выключить, то для времен}и начальное условие принимает вид: t t₁, n (n)₁. Тогда:

^t₁^
t t₁,

g_n 0


C_n (n)₁ exp^^_,

 n

^(t t₁) ^

и далее:

n(t)  (n)₁ exp^ ^.

 ^n 

(5)



p(t)  (p)₁exp^

(t t₁) ^

^. (6)




 __p

Ход этой зависимости показан на рис. 2.3 пунктирной линией.

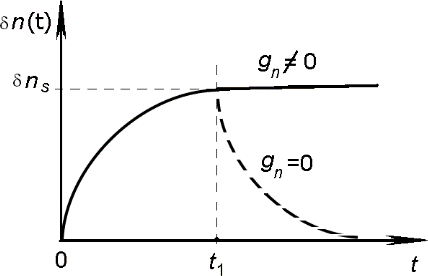
Рисунок 2.3

Выключение генерации носителей заряда приводит к тому, что избыточные концентрации электронов и дырок за счет процессов рекомбинации будут стремиться к своим равновесным значениям. Согласно выражениям 4 - 6, при

постоянных значениях параметров _nи  _pустановление избыточных концентраций

электронов и дырок в зонах разрешенных значений энергии, а также их исчезновение описываются экспоненциальным законом. Поэтому можно определить физический

смысл констант _nи  _pкак промежуток времени, в течение которого неравновесная

концентрация электронов (дырок) при включении или выключении источника генерации носителей заряда увеличивается или уменьшается в e- раз.

1 2 3 4 5

Фотопроводимость полупроводников

Собственная и примесная фотопроводимость
Возникновение неравновесных носителей проявляется в изменении электропроводности кристалла – в таких случаях говорят о возникновении фотопроводимости. Под фотопроводимостью полупроводника понимают изменение его проводимости, вызванное освещением полупроводника. Полупроводник, используемый для регистрации оптического излучения за счет возникновения в нем фотопроводимости, называют фоторезистором. Изменение проводимости может регистрироваться при приложении к фоторезистору как постоянного напряжения, так и переменного. В соответствии с этим различают фотопроводимость на постоянном токе и на переменном.

^{Физическая}^{причина}^{возникновения}^{фотопроводимости}^{полупроводника}

одна: изменение (возрастание) концентрации свободных носителей заряда ( n

и/или p) в разрешенных зонах энергии за счет поглощения падающего излучения.

Однако электронные переходы при оптической генерации могут быть различными. ^Если^{энергия}^{фотонов}  E_g^,^то^{неравновесные}^{электроны}^и^дырки^{образуются}^врезультате возбуждения электронов, переходящих из валентной зоны в зону проводимости, а также дырок, остающихся в валентной зоне. Это так называемая

собственная оптическая генерация и, соответственно, собственная фотопроводимость. Обратный процесс есть прямая рекомбинация «свободный электрон – свободная дырка». В результате оптической генерации в области собственного поглощения в полупроводнике образуется пара свободных носителей заряда противоположных знаков.

При наличии достаточного количества примесей в полупроводнике

фотопроводимость может возникать и при

  E_g^.^Тогда^при^{падении}^света^с

^^^^E_c^^E_d^,^гдеE_d

- энергия уровня донорной примеси, происходит возбуждение

электронов, связанных с примесью, в зону проводимости. В этом случае имеет место примесная оптическая генерация и, соответственно, в результате возникает

примесная фотопроводимость. Когда

  E_a E_v

возможна генерация дырок в

валентной зоне. Оба случая – случаи монополярной фотопроводимости, поскольку в результате освещения генерируются носители одного знака. Поглощение в собственной полосе длин волн на несколько порядков больше поглощения в примесной области.

Скорость оптической генерации – есть число электронов или дырок, генерируемое светом в единицу времени в единичном объеме. Она связана с коэффициентом поглощения света. Вычислим скорость генерации в полупроводнике. Пусть I(x) - монохроматический световой поток, приходящийся на единицу поверхности, на расстоянии xот освещаемой поверхности полупроводника, ^а ^–^{коэффициент}^{поглощения}^света.^Тогда^число^{фотонов,}^{поглощаемых}^вединицу времени в слое с единичной площадкой в слое, расположенном между слоями xи x+dx, есть разность интенсивностей света в этих точках:

dIx  Ix dx Ix  I_пр exp  x dx I_пр exp x 

 I_пр exp x I_пр exp   dx I_пр exp x  I_пр exp xI_пр exp   dx1

 Ix 1   dx1  Ix  dx

Здесь обозначено

I_пр I₀1 R, R- коэффициент отражения света от поверхности

полупроводника. В приведенном расчете проведено разложение экспоненциальной ^{функции}^в^ряд^{Тейлора}^по^{степеням}dx^вблизи^точкиx^.

Следовательно, число генерируемых светом электронов и дырок за единицу времени в кристалле единичной длины Lв направлении падающего света, равно

^I^^x^^^. Здесь введен безразмерный параметр  , называемый квантовым

выходом внутреннего фотоэффекта. Он равен числу пар свободных носителей, рождаемых в среднем одним поглощенным фотоном.

Скорость оптической генерации в кристалле имеет размерность штук/(cм³с). При этом коэффициент поглощения можно найти как величину, обратную длине

свободного пробега фотона

l_ф:

  1 l_ф. Тогда функция генерации неравновесных


^{носителей}^{заряда в}^точкеx^может^быть^{записана}^в^виде:





l
gx  1 R ^I⁰



exp^

^x^. (7)

_ф _l_ф

Из данного выражения следует, что в нем при единичной площади освещаемого полупроводника все генерируемые светом неравновесные электроны и дырки локализованы в пределах длины свободного пробега фотона. Такая ситуация в полупроводниках возможна, если полупроводник освещается короткими импульсами света и регистрация неравновесного состояния производится в течение времени, значительно меньшим времени жизни неравновеснных носителей заряда, так что они не успевают диффундировать в объем полупроводника на сколько-нибудь значительное расстояние по сравнению с длиной диффузии. В подавляющем числе практически значимых ситуаций регистрация неравновесного состояния проходит непрерывно или в течение большого промежутка времени. Поэтому влиянием диффузии неравновесных носителей на их распределение в объеме полупроводника пренебречь нельзя. Они оказываются распределенными от

освещаемой поверхности на длине диффузии (его размер в направлении регистрации света

L_диф. Если полупроводник толстый

d L_диф), то в выражении (7) вместо

длины свободного пробега фотона должна стоять длина диффузии. Для тонкого

полупроводника длиной образца.

d L_диф

в знаменателе (7) будет фигурировать толщина

^{Функция}^{генерации}^для^всего^{толстого}^{образца}^{площадью}S^,^{полностью}

освещаемого регистрируемым излучением, будет определяться выражением

d _I₀d



^ ₁

₁ ^

G S_gxdx 1 R S_exp ^

^xdx


₀^Lдиф ₀

__ _l_ф

^Lдиф^^_

_I₀^Lдиф
^^L_диф l_ф^^
^^Lдиф^^lф^^I₀^Y⁰

 1 R

S _exp ^

^xdx 1 R^

^S_expydy

^Lдиф

^^^lф^^Lдиф^^

^^lф^^Lдиф^^Lдиф

0

^L_диф l_ф^
 ^

_I₀

^ ^

^L_диф l_ф^^
 0

^l_ф^

 1 R^

^S1 exp^

^  1 R S^

^ I₀.

^^lф^^Lдиф^^Lдиф ^

 _l_ф_

^^Lдиф^

^^ ^^ ^^

Механизмы возникновения фотопроводимости.

Выражение для проводимости полупроводника, представляющее собой сумму проводимостей по зоне проводимости, создаваемой свободными электронами –  _n

, и проводимости по валентной зоне, создаваемой дырками –  _р:

^^^_n^^_p^^e^_nⁿ^^e^_p^p. (8)

При падении на полупроводник излучения с интенсивностью Iпроводимость полупроводника изменяется на некоторую величину I. Так как рассматриваются

только слабые световые потоки, то, согласно правилам дифференциального исчисления, без каких-либо дополнительных предположений можно вычислить полный дифференциал выражения (8):

I = en_n ep_p e_nn e_pp, (9)

где

_n,

_p_,

n, p

представляют собой полные дифференциалы от

соответствующих величин. Таким образом, согласно выражению (9), освещение полупроводника может изменить его проводимость двумя путями: изменив концентрации свободных носителей в зонах, а также изменив их подвижности. Однако относительное влияние этих двух причин в реальности оказывается различным. Действительно, возникающая при поглощении фотона пара «электрон – ^дырка»^{получает}^{некоторый}^{квазиимпульс}^и^{энергию}⁽  E_g^),^{которая}^идет^накинетическую энергию электрона. Если кинетическая энергия велика, то электрон быстро перемещается в междоузлии кристалла и испытывает множественные столкновения, происходящие чаще, чем у свободного электрона, находящегося

внизу зоны проводимости. Поэтому его избыточная энергия быстро растрачивается. В результате через некоторое время, именуемое временем релаксации энергии –

_E 10^¹²c

и которое много меньше

_n,

 _p, средняя энергия фотоэлектронов,

имевших в момент своего рождения большую кинетическую энергию, принимает значение, соответствующее температуре решетки. В таком случае говорят, что электрон термолизовался – его кинетическая энергия стала соответствовать температуре кристалла.

Таким образом, за время своей жизни фотоэлектроны в зоне успевают быстро термолизоваться (прийти в состояние термодинамического равновесия с решеткой), так что все их параметры в течение практически всего времени жизни будут такими же, как и у равновесных носителей. В этом случае подвижности фотоэлектронов равны подвижности темновых (равновесных) электронов. Значит, даже если

освещать полупроводник светом с

  E_g, то избыток энергии вызывает

изменение и концентрации носителей, и изменение их подвижностей, но через очень

короткое время _E_n,  _p

подвижности фотоносителей становятся такими же, что

и у темновых электронов и дырок. Следовательно, с высокой степенью точности можно считать, что в результате поглощения света в полупроводниках изменяются только концентрации свободных носителей заряда: электронов и (или) дырок. Тогда:

  e(_p p _n n).

^Будем^{считать,}^что^{происходит}^{однородная}^{генерация}^пар⁽^gn^=gp ⁼^g⁼^const)и что в полупроводнике нет тока. Тогда, умножая кинетические уравнения для

концентраций носителей в зонах (1) на

e_n,

e_p

и складывая их, получим:

^^ e( _p _n)g ^;

(10)

t _фп

где обозначено:

^фп

__nn

_nn

  _pp

 _pp^.

(11)

_n^ _p

Из уравнения (10) видно, что характеристическое время ^_фп

– время релаксации

фотопроводимости определяет время установления стационарного значения ^{фотопроводимости} ^при^{изменении}^{условий}^{освещения.}^В^{стационарном}состоянии фотопроводимость равна

^⁽^t^^_фп⁾^^_s^^e⁽^_n^^_p⁾^^g^^_фп. (12)

где

^фп

- его значение в стационарном состоянии, т.е. при установившихся

значениях p

^иn^.^Отсюда^видно,^что^чем^больше

_фп, тем больше

_s, т.е. тем

выше чувствительность полупроводника к оптическому излучению, т.к. выше уровень стационарного значения фотопроводимости (11). Однако при этом будет больше и время установления (или затухания) фотопроводимости, т.е. полупроводник будет более инерционен и им нельзя будет регистрировать быстрые процессы.

Полевые свойства фотопроводимости

Для измерения фотопроводимости и ее кинетики разработано много различных методик. Рассмотрим одну из них, блок-схема которой показана на рис.

4. Здесь фоторезистор, показанный сопротивлением Rи включенный последовательно с источником напряжения ^Vи нагрузочным сопротивлением r, освещается прерывистым светом. Модуляция интенсивности света может быть получена, например, с помощью вращающегося непрозрачного диска с прорезью. В

отсутствии освещения через фоторезистор течет ток:

j₀

V

R₀ r

, который создает

вх
на входе усилителя напряжение U⁰

 r j V

r _.

R₀ r

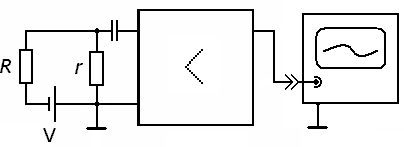
Рисунок 2.4

При освещении фоторезистора светом его сопротивление изменяется и становится равным R  R₀ R . Изменяется и ток во входной цепи и потому на входе усилителя появится дополнительное напряжение, связанное с освещением фоторезистора. Следовательно, полное напряжение на входе усилителя будет:

U_вх r j V

^r VR r

r

R₀ R r

 V ^r

(R₀ r)  R

V ^r

¹ U⁰^

R ^

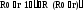вх¹



R₀ r^^.


Таким образом, при освещении полупроводника на входе усилителя появляется компонента во входном напряжении, пропорциональная интенсивности освещения и равная:

^вхR r
U_вх U⁰^^R.

0

Зная параметры входной цепи, теперь можно рассчитать величину фотопроводимости и ее изменение во времени.

вх

U
Анализируя проведенный расчет, можно сделать ряд полезных выводов. Данное выражение показывает, что величина сигнала от фотопроводимости тем

больше, чем больше значение

⁰^,^т.е.^чем^больше^{постоянное}^{напряжение}V^,

приложенное к фоторезистору через сопротивление нагрузки. Далее, нетрудно показать, что максимальный сигнал на входе усилителя достигается тогда, когда сопротивление сопротивления нагрузки и темновое сопротивление фоторезистора

равны:

R₀ r. Сигнал на входе усилителя будет:

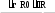U_вх U⁰^^R V^rR V .

^вхR₀ r

R₀ r²

1  r

R₀²^R0

Обозначим x r

R₀. Максимум U_вх(x) найдем дифференцированием этой функции

и приравниванием к нулю производной, что дает одно физически реализуемое

решение:

x1^.

Если T- длительность светового импульса, за которым следует затемнение фоторезистора такой же продолжительности, то общий период модуляции светового

потока составит 2T. Будем считать, что импульсы света достаточно длинные:

T_фп

и потому за время его действия фотопроводимость достигает своего

максимального значения

_s. На отрезке времени

(T;

2T)

генерация

неравновесных носителей заряда отсутствует, а доминирует рекомбинация ранее созданных фотоэлектронов и фотодырок. Потому фотопроводимость

полупроводника уменьшается от

_s

по экспоненциальному закону:

1 2 3 4 5

t
 




(t)  _s exp^ ^.

 __фп
Если ^_фппостоянно во времени, то  изменяется во времени так, как показано на рис. 2.5.

Кривые релаксации фотопроводимости могут быть использованы для определения параметров полупроводника. На начальном участке нарастания  в уравнении (9) можно пренебречь вторым слагаемым в правой части (  – мало). Тогда получим:

(t)  e(_n _p)gt.

Линейное увеличение фотопроводимости со временем освещения характеризуется наклоном, тангенс угла которого равен

tg()  e(_n _p)   I,

^где ^–^{квантовый}^выход, ^–^{коэффициент}^{поглощения.}

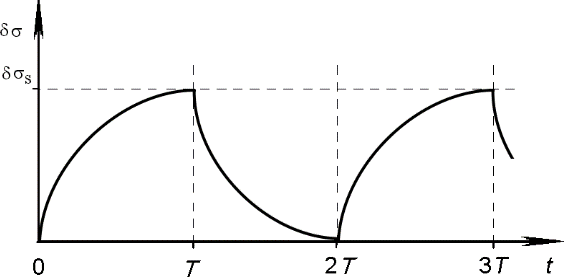Этот участок роста фотопроводимости не зависит от рекомбинации, а определяется только процессами генерации. Поэтому исследование начальной стадии нарастания фотопроводимости используют для определения квантового выхода  .

Рисунок 2.5

При выключении света спад фотопроводимости используют для определения времени релаксации фотопроводимости как время, за которое фотопроводимость

уменьшается от своего максимального значения

_s

в е- раз. Нарастающий

участок кинетических кривых фотопроводимости для определения времени релаксации не используют ввиду того, что из-за малого сигнала на начальном участке возникает большая ошибка в определении _фп. Спад фотопроводимости от

этого недостатка свободен из-за большого значения фотопроводимости в момент выключения света.

Коэффициент усиления фотопроводимости. Поскольку величина сигнала от фотопроводимости тем больше, чем больше приложенное постоянное напряжение, то резонно задаться вопросом: до каких значений можно увеличивать постоянное напряжение на фоторезисторе? Будем считать, что рассматриваемый полупроводниковый образец с омическими контактами на концах имеет длину L. В цепи с нагрузочным сопротивлением R (рис. 6) фототок при действии электрического поля E будет равен:

j_ф _s E,

j_ф e(_n  _p)  g_фп E.

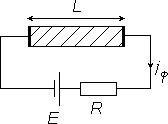
Рисунок 2.6 Если _n _p, то можно записать:

j_ф e(_n_n _p _p)  g E.

Введем в рассмотрение время пролета образца электроном и дыркой соответственно:

t_n ^L

v_n

 ^L;

_n E

t _p ^Lv_p

 ^L,

 _p E

где

v_n,

v_p– скорости электронов и дырок. Тогда будет:



 _t_n
j_ф e^





 _p

_n
 ^ L g.


_t_p

Обозначим:

K ^ⁿ ^^p

. Эта величина показывает, сколько раз за время своей

t_nt_p

жизни неравновесная электронно-дырочная пара может пролететь через весь образец, т.е. участвовать в фотопроводимости. С учетом этого:

j_Ф e K L g.

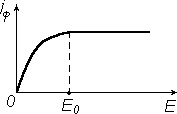
Если

Рисунок 2.7

K 1, то электрон и дырка успевают прорекомбинировать, не пролетев

полностью образец. Увеличив прикладываемое электрическое поле, можно ^{уменьшить}^tⁿ^и^t^p^{, а значит, увеличить}^j^ф. ^{Параметр}^K^{называют}^{коэффициентом}усиления фотопроводимости. При решении практических задач необходимо стремиться к тому, чтобы Kбыло максимальным. Зависимость величины фототока от приложенного поля обычно имеет вид, показанный на рис. 7. Величину ^{электрического}^поля^E0^,^при^{котором}^{достигается}^{предельное}^{значение}коэффициента усиления фотопроводимости, можно найти из условия:

t_n _n,

(t_p  _p)
_E₀_L

_n _n

или

V₀
_L2

.

_n _n

^{Увеличивать}^{напряжение}^на^{образце}V^выше^V₀

нецелесообразно, т.к. при

V V₀

через электрический контакт вытягиваются оба типа неравновесных носителей, и K

достигает максимального значения фотопроводимости).

^Kmax

(не больше двух для биполярной

Частотные свойства фотопроводимости

Если интенсивность падающего оптического излучения модулирована по гармоническому закону, то

g_n g₀exp^it^, g_p g₀expit. (13)

Изменения концентраций носителей заряда также подчиняются гармоническому закону изменения во времени на той же частоте, и поэтому решения кинетического уравнения (1) для концентраций носителей заряда будем отыскивать в виде

^ⁿ^^ⁿ₀^^exp^ⁱ^^t^^,p_p p₀ expit. (14)

Подставив выражения (13) и (14) в уравнения (1), найдем, что максимальные