Файл: Кафедра Электроэнергетика и электротехника Дисциплина Численные методы решения задач.docx

Федеральное государственное бюджетное образовательное учреждениевысшего образования«Саратовский государственный технический университет имени Гагарина Ю.А.»Кафедра «Электроэнергетика и электротехника»Дисциплина «Численные методы решения задач»КОНТРОЛЬНАЯ РАБОТАВыполнил: студент группы___________ Иванов П.Н. (дата) Проверил: _________________________ подпись И.О. Фамилия преподавателя (дата) Саратов 2023Оглавление

Вариант 6

Решить уравнение методом половинного деления и хорд с точностью ε = 0,00001.

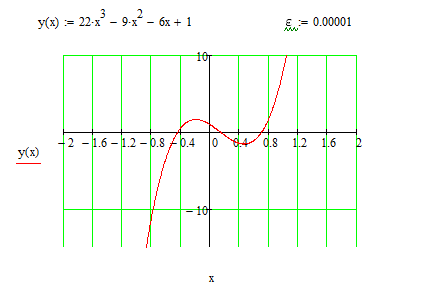
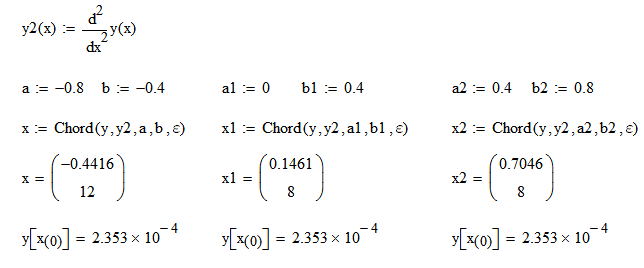
22х³ – 9х² – 6х + 1 = 0Построим график имеем три корня, локализованных на интервалах [-0.8;-0.4], [0;0.4] и [0.4;0.8]Ищем корниКорни уравнения х1 = -0.4416, х2 = 0.1461, х3 = 0.7046Число итераций = 16Корни уравнения х1 = -0.4416, х2 = 0.1461, х3 = 0.7046Число итераций = 12 и 8

Решить уравнение методом итерации с точностью ε = 0,00001.

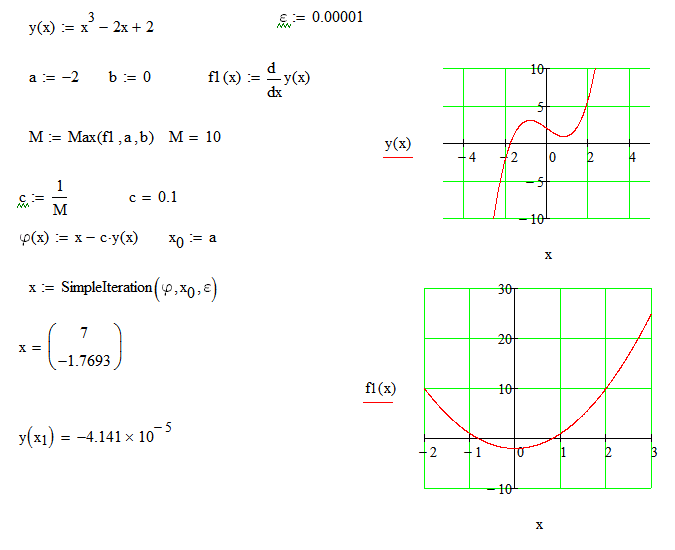
х³ - 2х + 2 =0Корень уравнения х = -1.7693Число итераций = 7

Решить уравнение методом Ньютона (касательных) с точностью ε = 0,00001.

х³ - 2х + 2 = 0

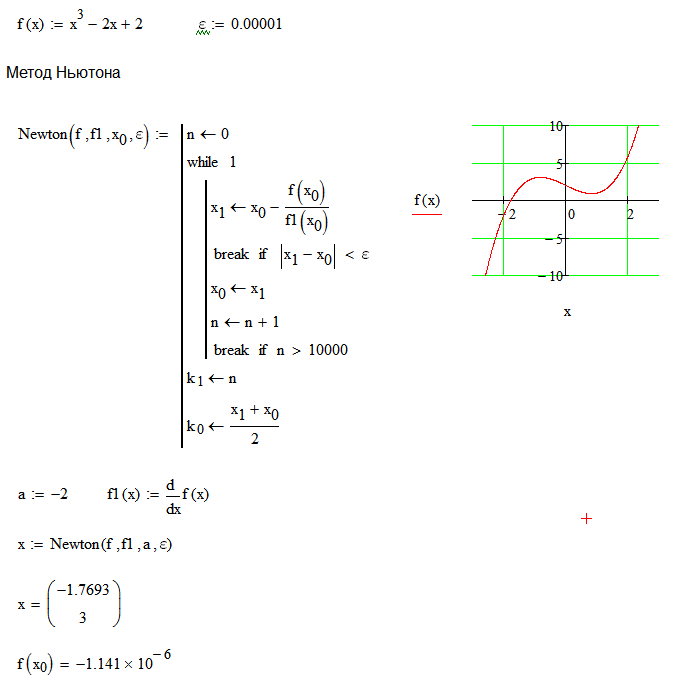
Решить уравнение видоизменённым методом Ньютона с точностью ε = 0,00001.

---

х³ – 0,2х² +0,5x - 1 = 0Корень уравнения х = 0.893Число итераций = 5

---