Файл: Учебное пособие в двух частях Часть Основы теории.doc

– постепенный отказ – связан с медленным изменением значений параметров объекта;

– систематический отказ – многократно повторяющийся однородный по определенным признакам отказ, появляющийся вследствие недостатков конструкции, процесса изготовления и т. д.

8. Причины возникновения отказов:

– конструкционный отказ – возникающий из-за недостатков конструкции;

– производственный (технологический) отказ – следствие ошибок, нарушений и несовершенства технологии;

– эксплуатационный отказ – следствие нарушений правил эксплуатации.

9. Значимость отказов:

– критический отказ – такой, при котором возникает угроза человеку или окружающей среде;

– существенный отказ – такой, при котором ухудшение эксплуатационных характеристик или полная непригодность объекта к эксплуатации не приводят к опасности для человека;

– несущественный отказ – такой, который имеет незначительные последствия, вызывающие недовольство.

10. Время возникновения отказов:

– приработочный отказ – появляется в начальный период эксплуа­тации;

– отказ при нормальной эксплуатации;

– отказ вследствие износа – появляется в заключительный период эксплуатации.

Вариант классификации отказов представлен на рис. 1.1.



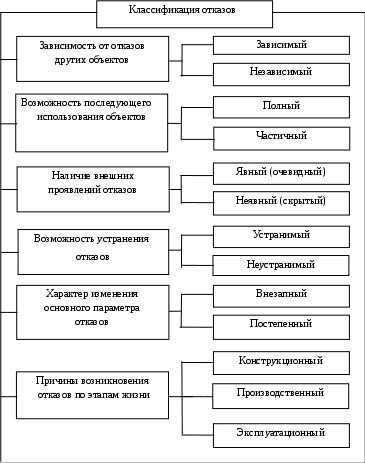
Рис. 1.1. Классификация отказов
Контрольные вопросы

1. Назовите основные этапы становления надёжности как науки.

2. В чем заключается понятие надёжности как свойства объекта?

3. Дайте определения основных состояний и событий, которыми характеризуется надёжность.

4. В чем общность и отличия состояний «исправность» и «работоспособность» объекта?

5. При каких условиях наступает предельное состояние объекта?

6. Какими могут быть объекты по пригодности к восстановлению работоспособного состояния?

7. Какими могут быть отказы по типу и природе происхождения?

8. По каким признакам классифицируют отказы?

9. Дайте определения свойств (составляющих) надёжности.

10. Перечислите и поясните показатели долговечности.

2. КРАТКОЕ ИЗЛОЖЕНИЕ
ОСНОВ ТЕОРИИ ВЕРОЯТНОСТЕЙ

2.1. Основные понятия и определения

Испытанием (опытом) называется одно из сколь угодно большого числа раз воспроизводимого определённого перечня (состава) условий.

---

Событие – совокупность явлений, происходящих в результате испы­тания.

Если событие происходит неизбежно в результате каждого испытания, оно называется достоверным.

Если событие не может произойти, оно называется невозможным.

Множество возможных при данном испытании и связанных с ним событий называется полем событий, а события этого поля – случайными событиями.

Случайное событие – всякий факт (исход), который может произойти или не произойти.

Выборкой называется небольшая часть некоторого множества объектов, отобранная наугад. При этом отобранные объекты правильно отражают качества и свойства элементов множества, что достигается в результате тщательного предварительного перемешивания (диспергирования) свойств. Отбор каждого элемента выборки является испытанием и завершается соответствующим событием.

Выборка с возвращением – при последовательном выборе шаров из урны после каждого выбора взятый шар возвращается в урну.

Выборка без возвращения – из урны выбирается некоторое количество шаров без возвращения.

Пусть n – число элементов выборки от 1 до n. Осуществление выборки представляет собой поле событий

А₁,А₂,…, А_n, (2.1)

где А_n – отбор n-го элемента, а события поля равновозможны.

События поля могут быть элементарными и сложными. Сложному событию А_n{n₁,n₂,…,n_k}, где n₁<n₂<…< n_k – номера элементарных событий, составляющих сложное, соответствует появление событий с номерами n₁, или n₂, или n_k. Здесь каждому событию А_n соответствует некоторое количество (или подмножество) элементарных событий.

Говорят, что событие А влечёт за собой событие В (из А следует В), если при наступлении А неизбежно наступление В.

Если из А следует Ви одновременно из В следует А, то событияА и В эквивалентны, илиА = В.

Каждое событие поля представляет собой подмножество некоторых событий из множества (А₁,А₂,…,А_n). Например, событие В, состоящее в появлении номеров 2, 5, 7, принято обозначать В{2, 5, 7}. Его записывают как логическую сумму

---

В = А₂+А₅+ А₇, (2.2)

где «+» равнозначен союзу «или».

В данном случае можно событие В представить как сумму двух событий

В = {2, 5} + {7}

илиВ = (А₂+А₅) + А₇. (2.3)

Событие В является также суммой несовместных событий, так как события {2, 5} и {7} не могут произойти в одном испытании. Совместными являются события {1, 2, 3, 4} и {4, 5, 6, 7}, они наступают вместе в тех испытаниях,
в которых появляется номер 4. Сумма {1, 2, 3} + {1, 2} тождественна событию {1, 2, 3}.

Сумма любых двух событий поля есть событие того же поля.

Полю всегда принадлежит достоверное событие S{1, 2, … n}, заключающееся в том, что выбирается один из номеров от 1 до n. События «–n»,…,
«–1»,0,n+1 невозможны и обозначаются («не А»).

События А и – взаимно дополнительны или противоположны, если они несовместны и составляют в сумме достоверное событие, т. е. достоверно то, что наступит А или .

Под произведением событий А₁,А₂,…, А_nпонимается одновременное наступление их всех, т. е. когда А₁,и А₂, и … и А_n наступают вместе.

Произведением двух событий С{1, 2, 3, 4} и D{2, 4, 6, 8} является событие Е = СD = {2, 4}.

Случайной называется величина, которая может принять какое-либо неизвестное заранее возможное значение, зависящее от случайных факторов, не поддающихся учету (обозначается ).

Случайные величины могут быть прерывными (дискретными) и непрерывными.

Прерывными (дискретными) называются величины, которые принимают отделённые друг от друга значения.

Непрерывными называются величины, возможные значения которых заполняют непрерывно некоторый конечный или бесконечный промежуток (ресурс).

Относительная частота. Пусть проводится серия из N испытаний в одинаковых условиях. Если интересующее нас событие, например

---

А,произошло раз, то отношение

(2.4)

называется относительной частотой появления события А в данной серии испытаний. Очевидным является то, что

, (2.5)

для невозможного события, для достоверного события.

Вероятность. Каждому из событий можно поставить в соответствие
определенное число, называемое его вероятностью Р = Р(«А»)или
Q = Р(«не А»)и являющееся мерой возможного совершения этого события.

Вероятность есть численная мера, характеристика возможности появления события в диапазоне значений 0…1.

. (2.6)

Вероятность достоверного события равна единице

. (2.7)

Вероятность противоположного события дополняет вероятность данного события до единицы

, (2.8)

где А и – противоположные события.

Вероятность невозможного события равна нулю

. (2.9)

Сумма вероятностей несовместных событий, составляющих полную группу, равна единице

, (2.10)

где А₁, А₂, … А_n– несовместные события, составляющие достоверное событие (полную группу событий).

Классическое определение вероятности: вероятность события А есть отношение числа m благоприятствующих этому событию исходов к общему числу nвсех возможных элементарных несовместных и равновозможных исходов испытания.

. (2.11)

В большой серии испытаний относительная частота

---

(А) приближается к вероятности P(А).

2.2. Теорема сложения вероятностей

Вероятность появления какого-либо из нескольких несовместных событий равна сумме вероятностей каждого из этих событий:

. (2.12)

Следствие 1: сумма вероятностей всех возможных событий, составляющих данное событие, равна единице.

Следствие 2: сумма вероятностей двух противоположных событий равна единице.

. (2.13)

Условная вероятность события А при наступлении события В – вероятность событияА, вычисленная в предположении, что событие В произошло:

. (2.14)

2.3. Теоремы умножения вероятностей

Теорема умножения вероятностей зависимых событий:

. (2.15)

Теорема умножения вероятностей независимых событий:

. (2.16)

На основании теорем сложения и умножения вероятностей составляется общее правило сложения вероятностей: вероятность суммы двух событий (совместных или несовместных) равна сумме вероятностей этих событий без вероятности совместного их наступления:

. (2.17)

Для несовместных событий и (2.17) приводится к (2.12).

2.4. Теорема о повторении опытов

Следствием правил сложения и умножения вероятностей является теорема о повторении опытов (схема Бернулли): опыты считаются независимыми, если вероятность того или иного исхода каждого из них не зависит от того, какие исходы имели другие опыты.

Пусть в некотором опыте вероятность события Аравна P(А) = p, а вероятность того, что оно не произойдет, P( ) = q, причём

. (2.18)

Если проводится n независимых опытов, в каждом из которых событие

---