Файл: Учебное пособие в двух частях Часть Основы теории.doc

Решение:

,

.
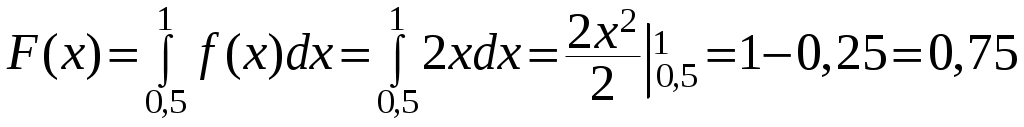Контрольные вопросы и задачи

1. Почему надёжность необходимо рассматривать в вероятностном аспекте?

2. Как можно подсчитать вероятность безотказной работы через число отказавших объектов и общее число объектов?

3. Какими способами задаются случайные величины?

4. Перечислите и поясните основные теоремы вероятности.

5. Назовите следствия основных теорем теории вероятностей.

6. Закон распределения случайной величины задан в виде таблицы:

х	–2	1	3	2
Р(х)	0,2	0,1	0,4	0,3

Известно, что M(x) = 0.

Найти D(x), (x), ν(x), M(x²).

7. Функция распределения имеет вид:


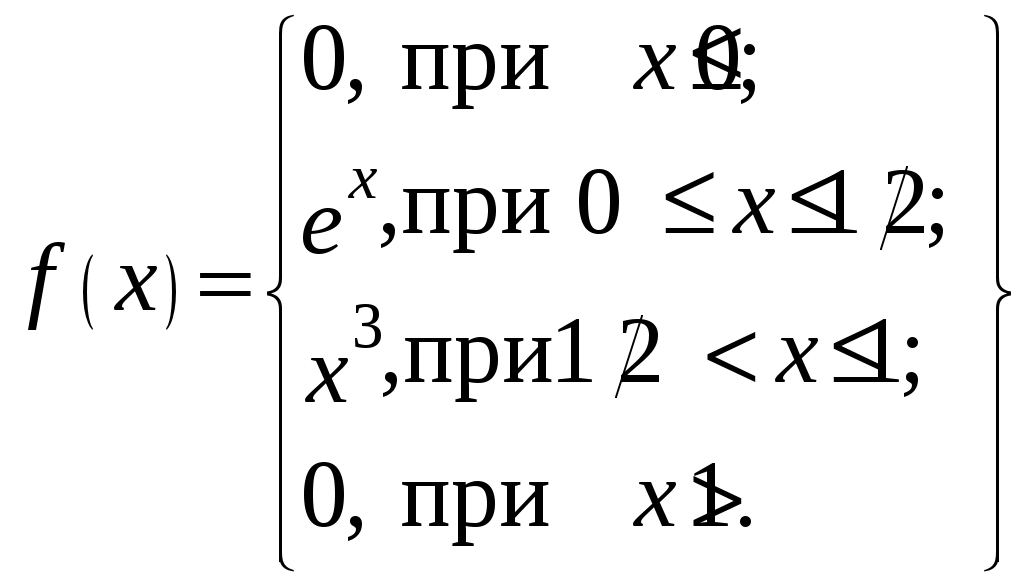
Найти вероятность того, что вероятность примет значение из диапазона

(¹/₃; ²/₃).

8. Прибор работает в двух режимах: «1» и «2». Режим «1» наблюдается в 60 % случаев, режим «2» – в 40 % случаев за время работы T. В режиме «1» прибор отказывает с вероятностью, равной 0,3, а в режиме «2» – с вероятностью 0,5. Определить вероятность отказа прибора за время T. Ответ: 0,38.

9. Прибор (рис. 2.5) состоит из трех блоков, которые независимо друг от друга могут отказать. Отказ каждого из блоков приводит к отказу всего прибора. Вероятность того, что за время T работы прибора откажет первый блок, равна 0,15, второй – 0,25, третий – 0,1. Найти вероятность того, что время T прибор проработает безотказно.

Ответ: 0,57375.



Рис. 2.5. Схема прибора
10. Прибор (рис. 2.6) состоит из двух блоков, дублирующих друг друга. Вероятность того, что время T каждый из блоков проработает безотказно, равна 0,9. Отказ прибора произойдет при отказе обоих блоков. Найти вероятность того, что время T прибор проработает безотказно.

---

Ответ: 0,99.

Рис. 2.6. Схема прибора
3. Показатели безотказности объекта

3.1. Предварительные сведения

Безотказность и другие свойства надёжности проявляются через случайные величины: наработку до отказа (наработку между отказами) и количество отказов за заданное время. Поэтому количественными характеристиками здесь выступают вероятностные переменные.

Наработка– продолжительность (объём) работы объекта. Измеряется в любых неубывающих величинах (единица времени, число циклов нагружений, километры пробега и т. п.). Объект может работать непрерывно (с учётом перерывов на ремонт) или с перерывами, не зависящими от технического состояния (в этом случае различают непрерывную и суммарную наработки).

Появление отказов не предопределено заранее, т. е. случайно, поэтому теория надежности основана на математическом аппарате теории вероятностей и математической статистики.

Для оценки надёжности проводятся эксплуатационные испытания значительного числа N элементов в течение времени t. Пусть к концу испытаний остается N_р работоспособных элементов и n отказавших.

Тогда относительное количество отказов:

. (3.1)

Вероятность безотказной работы оценивается относительным количеством работоспособных элементов:

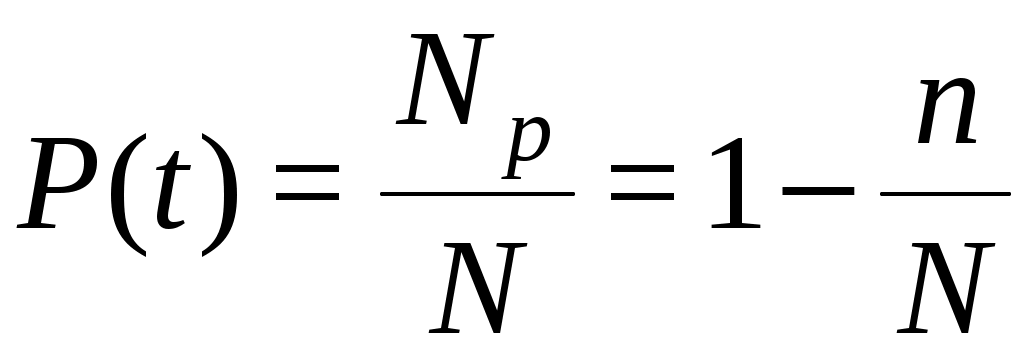. (3.2)

Вероятность безотказной работы (ВБР) означает, что в пределах заданной наработки отказ объекта не возникнет.

Так как безотказная работа и отказ – взаимно противоположные события, то сумма их вероятностей равна единице:

P(T) + Q(t) = 1,

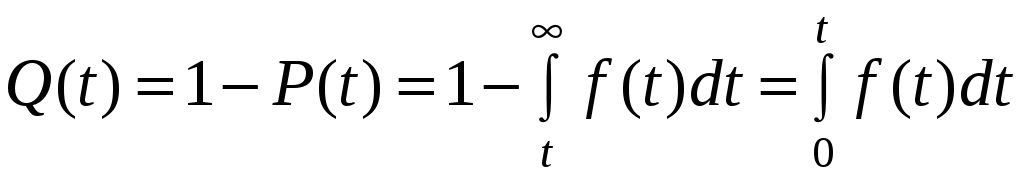=F(t).

F(t) есть интегральная функция распределения случайной наработки t.

Так как события, заключающиеся в том, что наступил или не наступил отказ к моменту наработки t, являются противоположными, то нетрудно убедиться, что P(t) является убывающей, а Q

---

(t) – возрастающей функцией наработки (рис. 3.1).



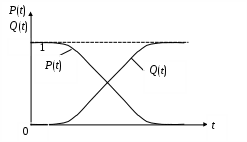
Рис. 3.1. Изображения функций P(t) и Q(t)
Действительно: а) в момент начала испытаний (t = 0) число работоспособных объектов равно общему их числу N(t) = N(0) = N,
а число отказавших – n(t) = n(0) = 0,

поэтомуP(t) =P(0) = 1,аQ(t) =Q(0) = 0;

б) при наработке t, возрастающей до бесконечности (t ∞), все объекты, поставленные на испытания, откажут, т. е.

N(∞) = 0, а n(∞) = N, поэтому P(t) =P(∞) = 0,аQ(t) =Q(∞) = 1.

Вероятность безотказной работы есть количественная мера того, что случайная величина наработки до отказа Tокажется не меньше некоторой заданной наработки t, еслиt ≥0:

P(t) = P{T ≥ t}. (3.3)

Очевидно, что Q(t) является функцией распределения случайной величины T и представляет собой вероятность того, что наработка до отказа окажется меньше некоторой заданной наработки t:

Q(t) = P{T < t}. (3.4)

Пример 3.1. Найти P(t) в интервале наработки [t, t + ∆t] при условии, что объект безотказно проработал до начала t интервала.

Решение:

Вероятность определяется посредством использования теоремы умножения вероятностей и выделения следующих событий:

A = {безотказная работа объекта до момента t};

B = {безотказная работа объекта в интервале ∆t};

C =A·B = {безотказная работа объекта до моментаt + ∆t}.

Очевидно, что P(C) = P(A·B) = P(A)·P(B/A), поскольку события A и B будут зависимыми.

Условная вероятность P(B/A)представляетP(t, t + ∆t) в интервале
[t,t + ∆t], поэтому

P(B / A) = P(t, t + ∆t) = P(C) / P(A) = P(t + ∆t) / P(t). (3.5)

Q(t) в интервале наработки [t, t + ∆t], с учётом (3.5), равна:

Q(t, t + ∆t) = 1 – P(t, t + ∆t) = [P(t ) – P(t + ∆t)] / P(t). (3.6)

Все изделия являются либо невосстанавливаемыми, либо восстанавливаемыми.

3.2. Показатели безотказности
невосстанавливаемых объектов

---

Невосстанавливаемыми называются такие объекты, для которых восстановление работоспособного состояния не предусмотрено в нормативно-техни­ческой и (или) конструкторской (проектной) документации [7].

Если происходит отказ такого изделия, то выполняемая операция будет сорвана, и ее необходи­мо начинать вновь в том случае, если возможно устранение отказа.

К таким изделиям относятся как изделия однократного действия (ракеты, управляемые снаряды, искусственные спутники Земли, усилители системы под­водной межконтинентальной связи и т. п.), так и изделия многократного действия (некоторые системы навигацион­ного комплекса судового оборудования, системы ПВО, системы управления воздушным движением, системы управления химическими, металлургическими и другими ответственными производственными процессами и т. д.).

Для невосстанавливаемых объектов применяется понятие наработка до отказа (он же является и последним отказом).

В расчетах пользуются средней наработкой до отказа, определяемой в [7] как математическое ожидание наработки объекта до первого отказа.

Средняя наработка до отказа Т₁ вычисляется по формуле

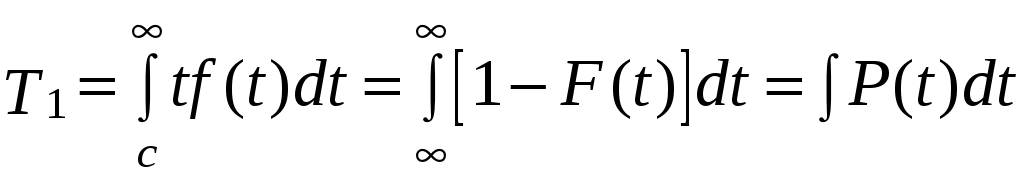, (3.7)

где F(t) –функция распределения наработки до отказа;

Р(t) – вероятность безотказной работы;

f(t)– плотность распределения наработки до отказа.

Статистически средняя наработка до отказа определяется по формуле

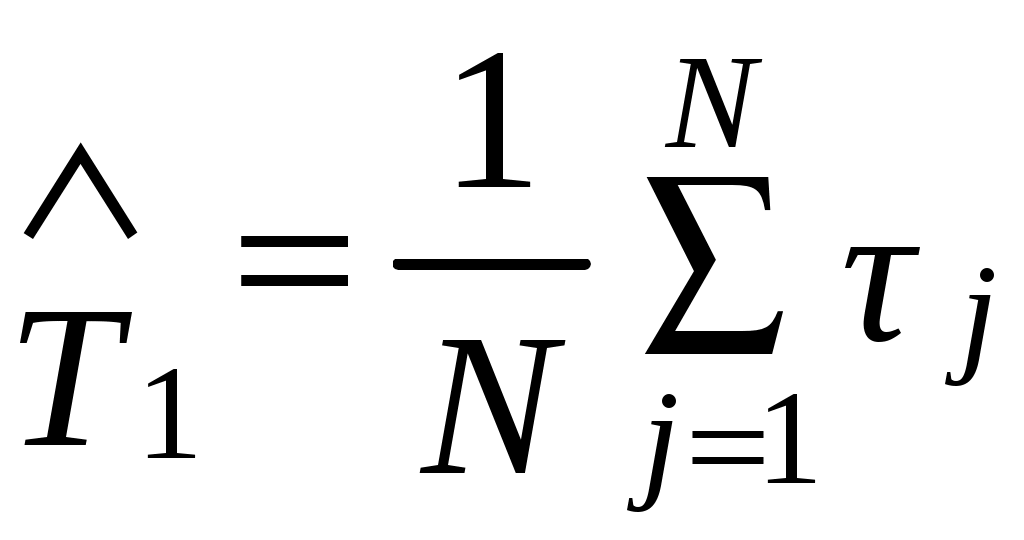, (3.8)

где N – число работоспособных объектов при t= 0;

– наработка до первого отказа каждого из объектов.

Длядифференцируемых функций распределения случайной величины определяется первая производная, называемая плотностью распределения
(законом распределения) времени работы объекта до отказа:

. (3.9)

Другим важным показателем надежности является интенсивность отказов, котораясообщает, какая часть объектов выходит из строя в единицу времени относительно среднего числа исправно работающих объектов.

Интенсивность отказов как статистический параметр – отношение числа отказавших объектов в единицу времени к числу объектов, продолжающих безотказно работать в данный промежуток времени:

---

, (3.10)

где Δn(Δt)– число отказавших объектов за промежуток времени от (t–Δt / 2)до (t+Δt / 2),

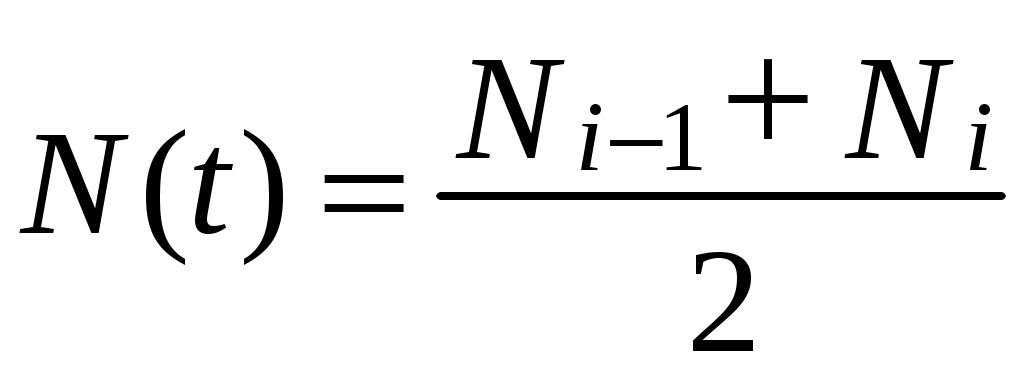, (3.11)

гдеN_{i – 1} – число исправно работающих объектов в начале интервала Δt;

N_i– число исправно работающих объектов в конце интервала Δt.

Интенсивность отказов как вероятностный параметр – условная плотность вероятности возникновения отказа изделия при условии, что до рассматриваемого момента времени t отказ не возник [7]:

, (3.12)

где функции f(t) и λ(t) измеряются в часах в минус первой степени.

При интегрировании (3.12) получается:

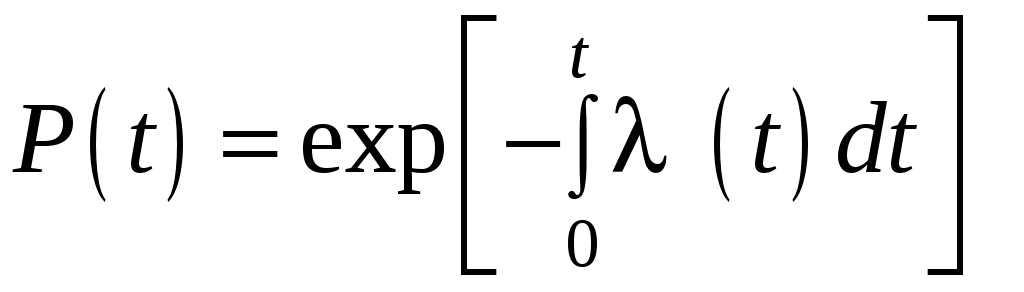. (3.13)

Величина λ(t)dt есть вероятность того, что элемент, безотказно проработавший в интервале наработки [0, t], откажет в интервале [t, t + dt].

Выражение (3.12), называемое основным законом надежности, позволяет установить временное изменение вероятности безотказной работы при любом характере изменения интенсивности отказов во времени.

В частном случае постоянства интенсивности отказов λ(t) = = const выражение (3.12) преобразуется в известное в теории вероятностей экспоненциальное распределение



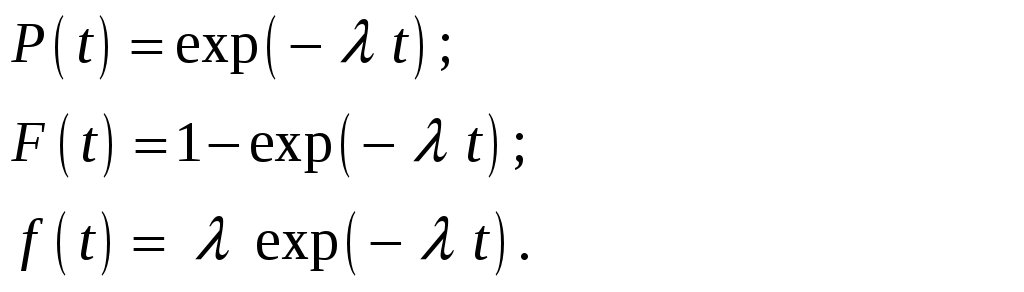
Таким образом, для невосстанавливаемых объектов применяют показатели Р(t), Т₁,f(t), λ(t).
3.3. Показатели безотказности
восстанавливаемых объектов

Восстанавливаемыми называются изделия, ко­торые в процессе выполнения своих функций допускают ремонт. Если произойдет отказ такого изделия, то он вы­зовет прекращение функционирования изделия только на период устранения отказа. К таким изделиям относятся: телевизор, агрегат питания, станок, автомобиль, трактор и т. п.

Величина λ(t)dt есть вероятность того, что элемент, безотказно проработавший в интервале наработки [0, t], откажет в интервале [t, t + dt

---