ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 951
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
А появляется с вероятностью p, то вероятность того, что в данной серии опытов событие А появляется ровно m раз, определяется по выражению
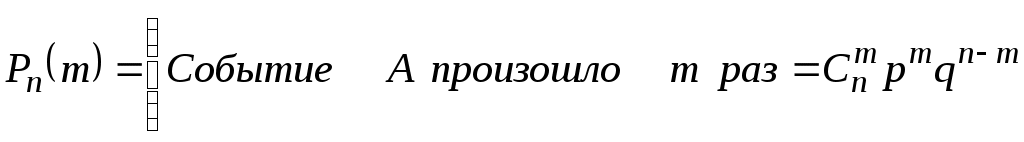 , (2.19)
, (2.19)
где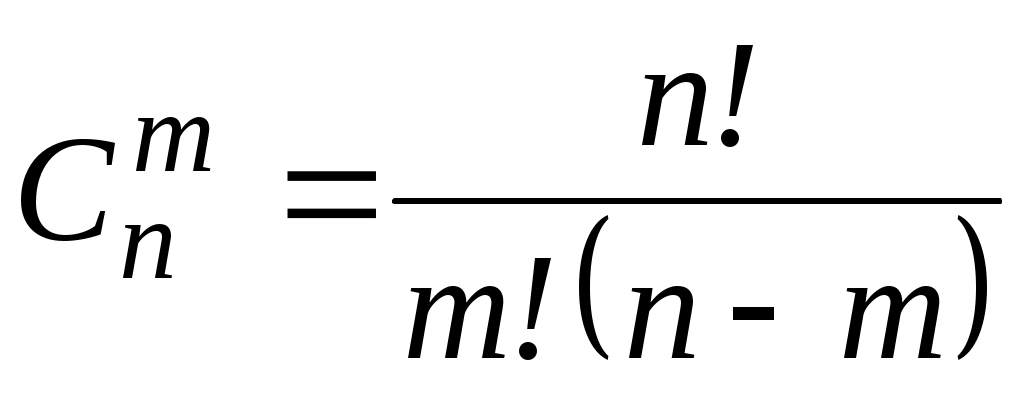 – биномиальный коэффициент. (2.20)
– биномиальный коэффициент. (2.20)
Например, вероятность отсутствия ошибки чтения 32-разрядного слова в формате ЭВМ, представляющего комбинацию 0 и 1, при вероятности ошибки чтения двоичного числа p = 10–3 составляет по (2.8) при m = 0,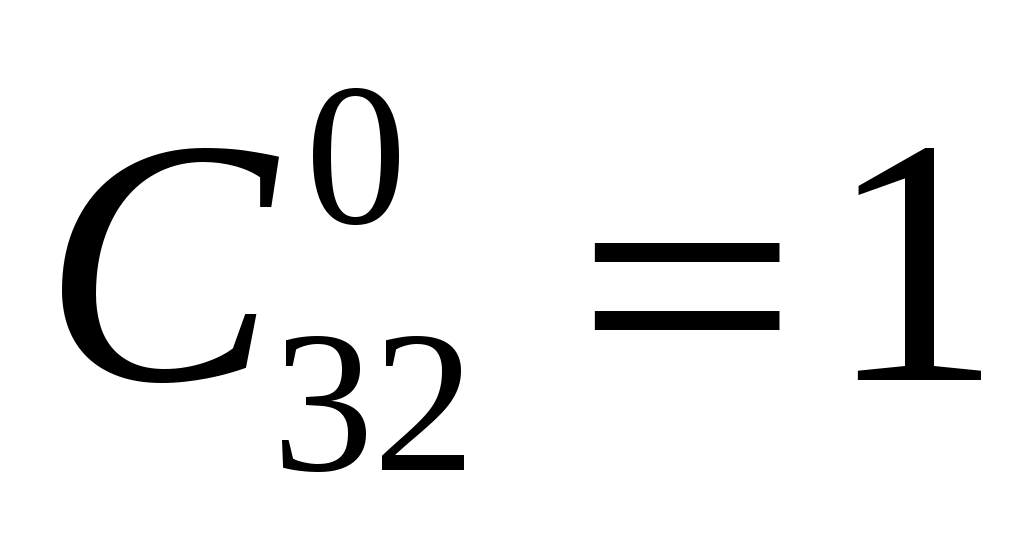 :
:
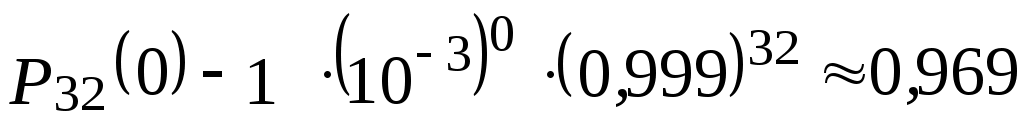 .
.
При больших m вычисление биномиальных коэффициентов Cnm и возведение в большие степени p и q связано со значительными трудностями, поэтому целесообразно применять упрощенные способы расчётов. Приближение,
называемое теоремой Муавра – Лапласа, используется, если npq>>1,
а |m – np|<(npq)0,5, в таком случае выражение (2.19) записывается:
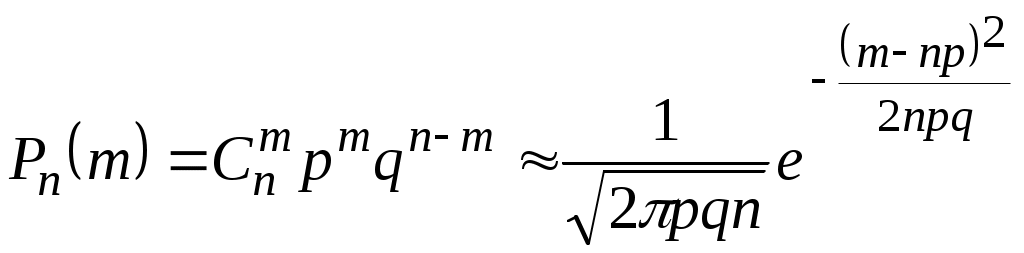 . (2.21)
. (2.21)
2.5. Формула полной вероятности
Если по результатам опыта можно сделать n исключающих друг друга предположений (гипотез) H1, H2, …, Hn, представляющих полную группу несовместных событий, то вероятность события А, которое может появиться только с одной из этих гипотез, определяется:
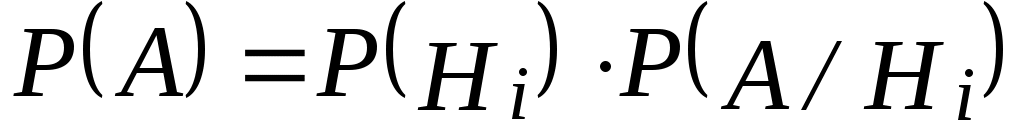 , (2.22)
, (2.22)
где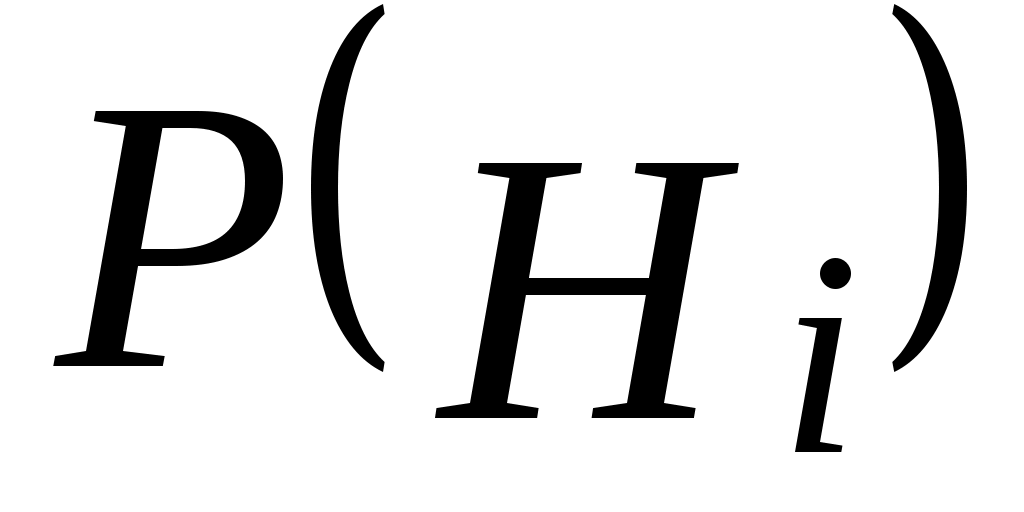 – вероятность гипотезы Hi;
– вероятность гипотезы Hi;
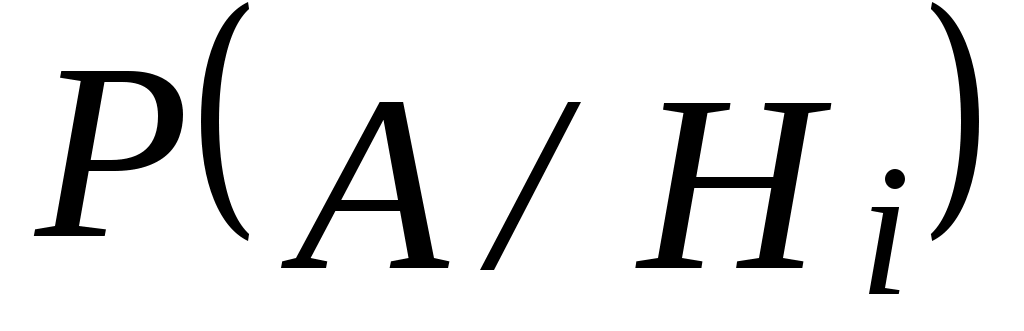 – условная вероятность события А при гипотезе
– условная вероятность события А при гипотезе 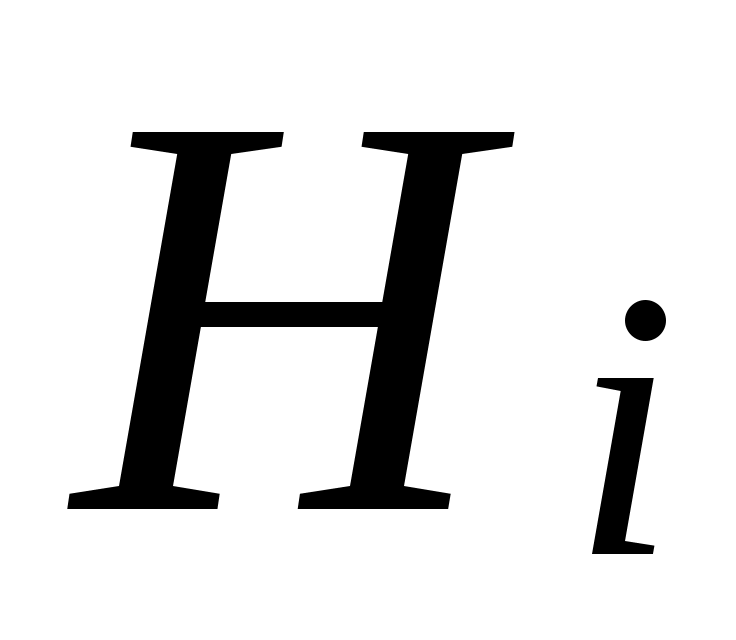 .
.
Поскольку событиеА может появиться с одной из гипотез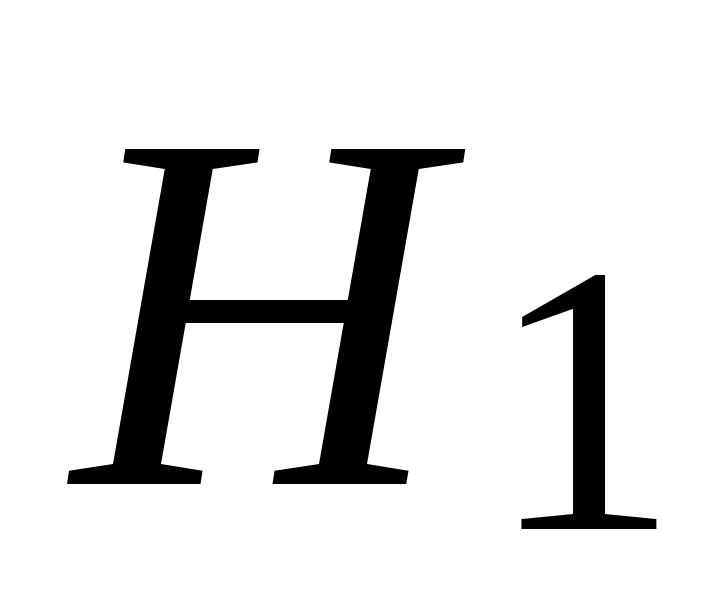 ,
, 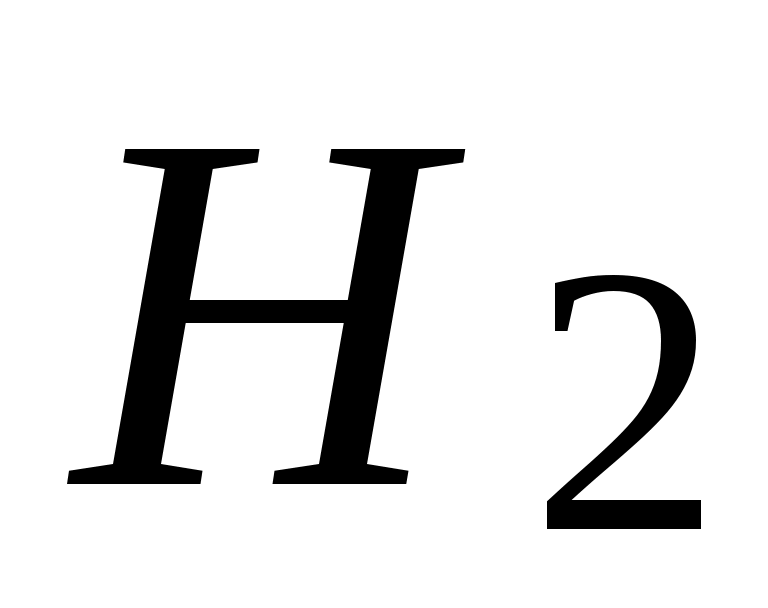 ,
,
…,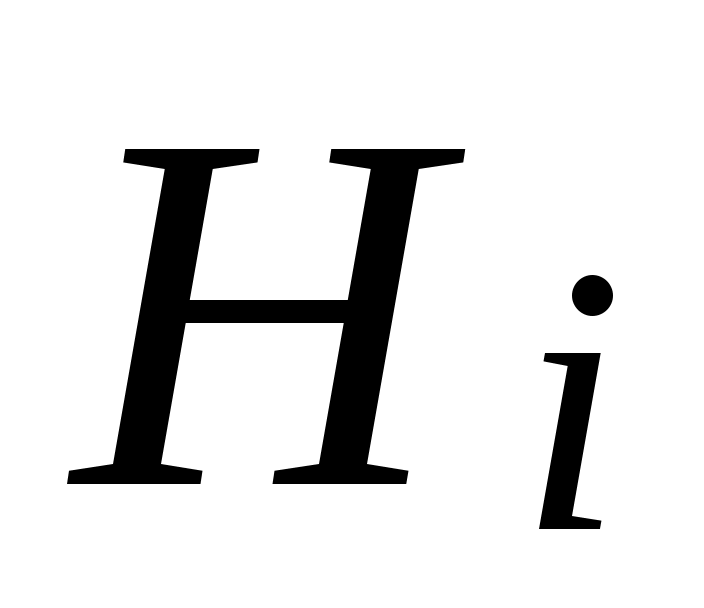 , то
, то
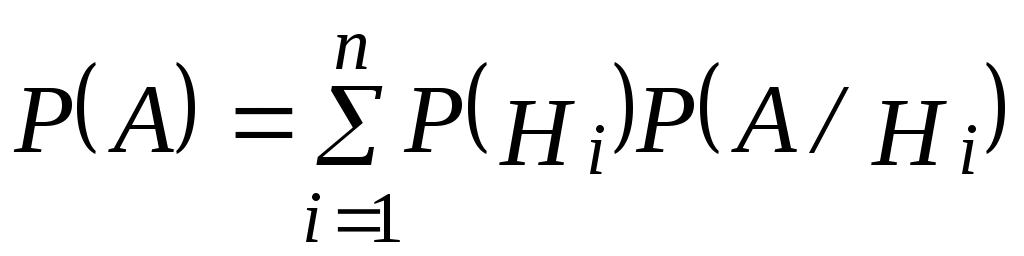
. (2.23)
2.6. Формула Байеса (формула вероятностей гипотез)
Если до опыта вероятности гипотез H1, H2, … Hn были равны P(H1), P(H2), …,P(Hn), а в результате опыта произошло событие А, то новые (условные) вероятности гипотез вычисляются:
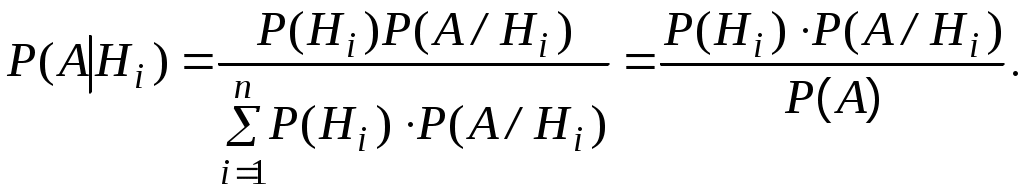 (2.24)
(2.24)
Доопытные (первоначальные) вероятности гипотез P(H1), P(H2), …, P(Hn) называютсяаприорными, а послеопытные – P(H1/А), Р(Н2/А), …,
P(Hn / А) – апостериорными.
Законом распределения вероятности случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Для получения закона распределения используют три способа:
–
– для дискретных величин;
табличный (табл. 2.1)
– графический (рис. 2.1)
– аналитический – для непрерывных величин.
Таблица 2.1
Табличный закон распределения

Рис. 2.1. Многоугольник распределения
Для непрерывных величин табличный способ не применяется. Непрерывные случайные величины задаются функцией распределения (рис. 2.2):
F(x) = P(x1,).

Рис. 2.2. Функция распределения непрерывной случайной величины
Функция распределения имеет ряд свойств:
1) она является неубывающей функцией ее аргумента, т. е. при х2 > х1
F(х2) > F(x1);
2) на минус бесконечности функция распределения равна нулю
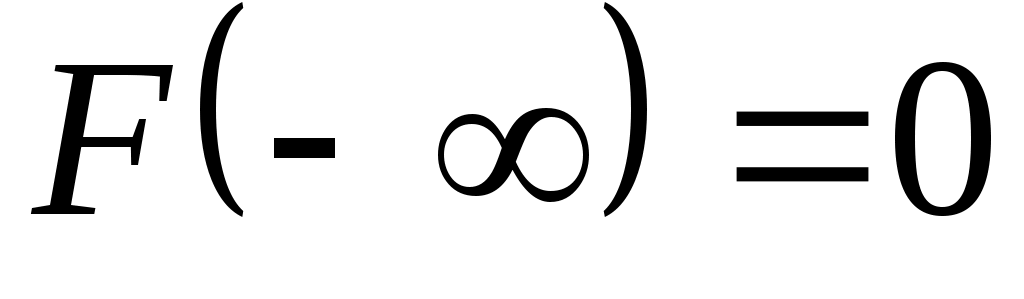 ;
;
3) на плюс бесконечности функция распределения равна единице
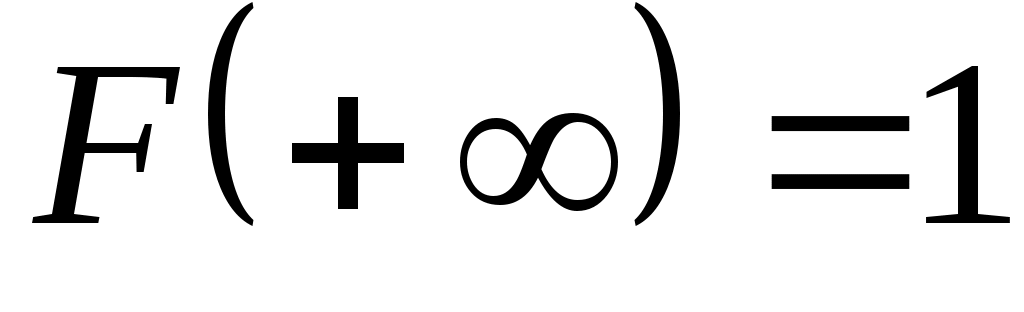 .
.
Плотность распределения («плотность вероятности») – первая производная от функции распределения. Другие названия: «дифференциальная функция распределения», «дифференциальный закон распределения».
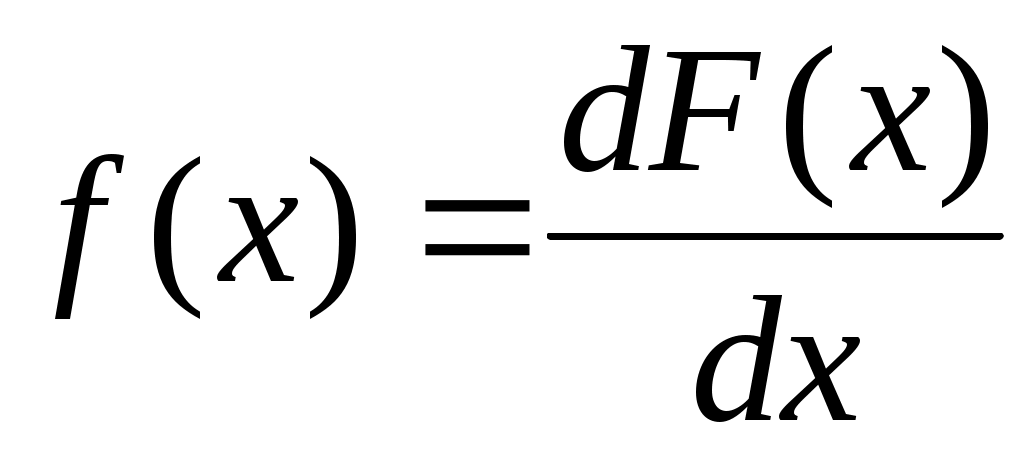 . (2.25)
. (2.25)
Плотность распределения изображается кривой распределения и показывает, как по оси абсцисс распределяются массы, т. е. кривая проходит через концы абсцисс значений «линейной плотности» (рис. 2.3).
Свойства плотности распределения:
1) плотность распределения – функция неотрицательная:
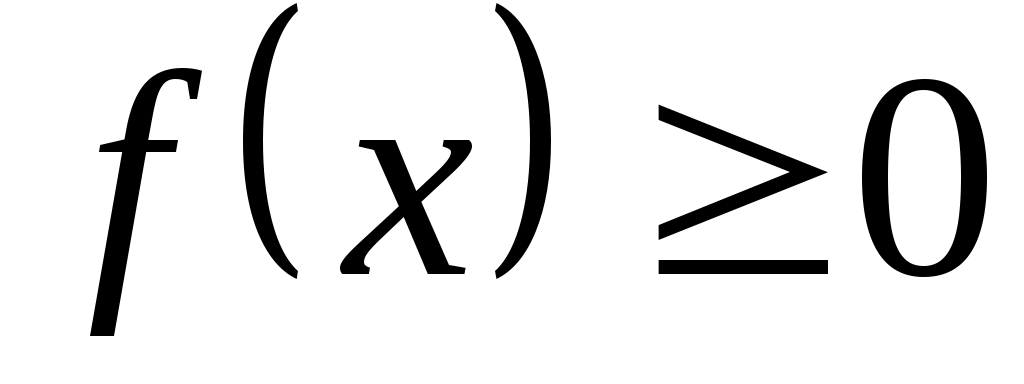 ;
;
2) интеграл в бесконечных пределах от плотности распределения равен единице:
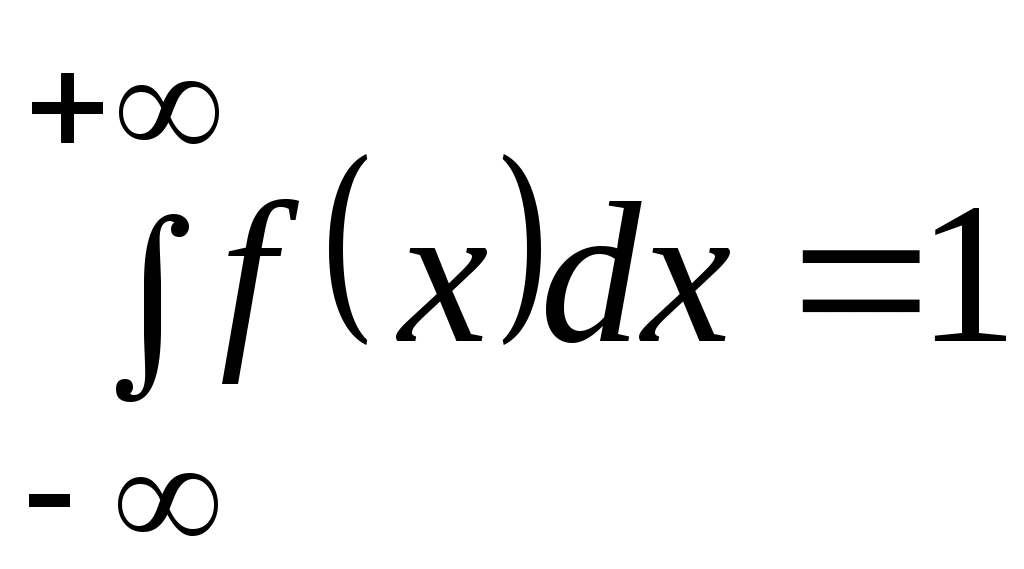 .
.

Рис. 2.3. Плотность распределения
Согласно свойству 2, функция распределения в интервале от 0 до х1
(рис. 2.4) определяется как интеграл плотности распределения
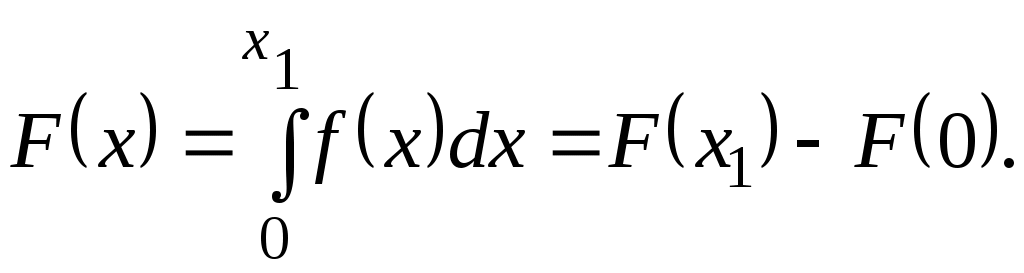 (2.26)
(2.26)
Рис. 2.4. Определение функции распределения
В ряде случаев бывает достаточно указать числовые характеристики.
2.8. Числовые характеристики случайных величин
1. Математическое ожидание – характеристика центра группирования случайных величин:
– для дискретных случайных величин
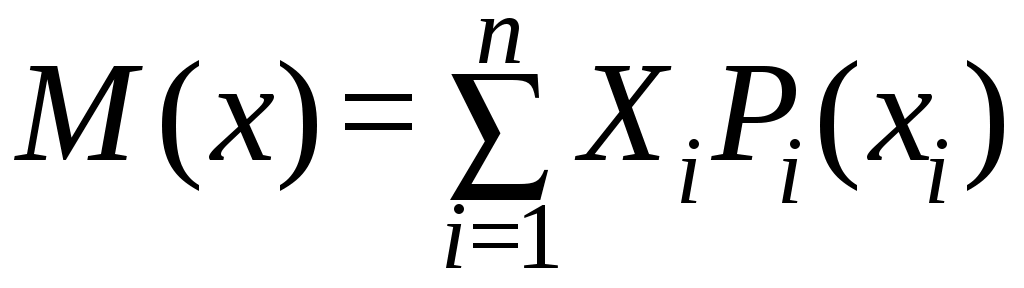 ; (2.27)
; (2.27)
– для непрерывных случайных величин
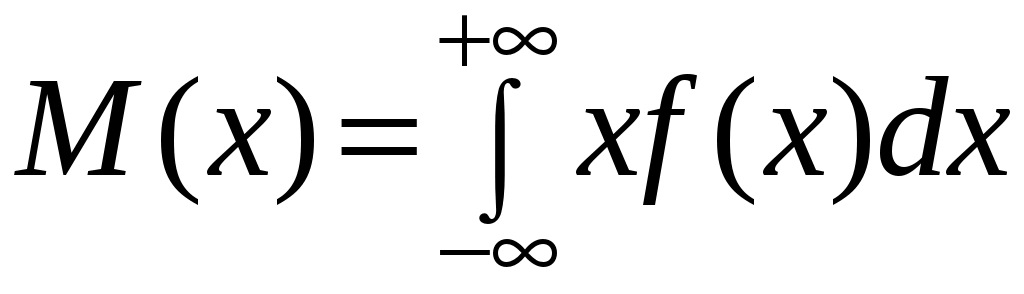 . (2.28)
. (2.28)
2. Модой непрерывной случайной величины называется то её значение,
в котором плотность вероятности наибольшая (т. М на рис. 2.4), М является точкой перегиба кривой.Модойдискретной случайной величины называется ее наиболее вероятное значение.
3. Медианой случайной величины Х называется такое её значение, для которого ограниченная кривой распределения площадь делится пополам (т. Ме на рис. 2.4). Площади справа и слева от медианы равны.Можно также определить медиану случайной величины X как такое ее значение Me, для которого
P(X<Me) = P(X>Me). В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.
4. Значение случайной величины, соответствующее заданной вероятности, называется квантилью. Квантиль при вероятности, равной 0,5, называется
медианой.
5. Дисперсия есть сумма произведений квадратов разностей случайных величин и математических ожиданий:
– для дискретных случайных величин
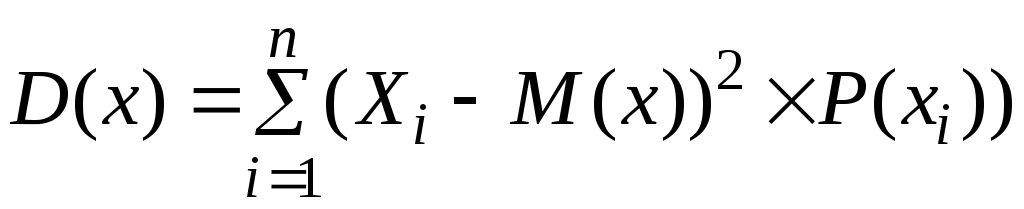 ; (2.29)
; (2.29)
– для непрерывных случайных величин:
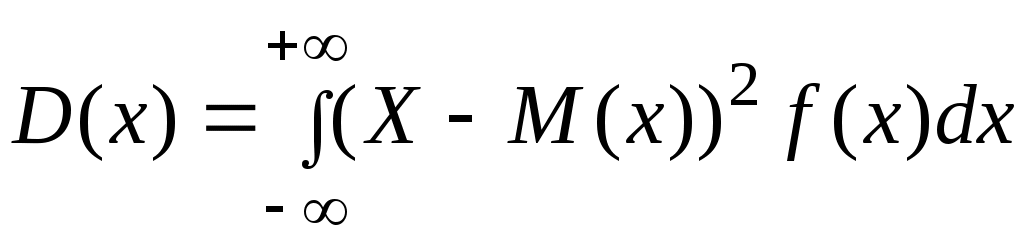 . (2.30)
. (2.30)
6. Среднее квадратическое отклонение
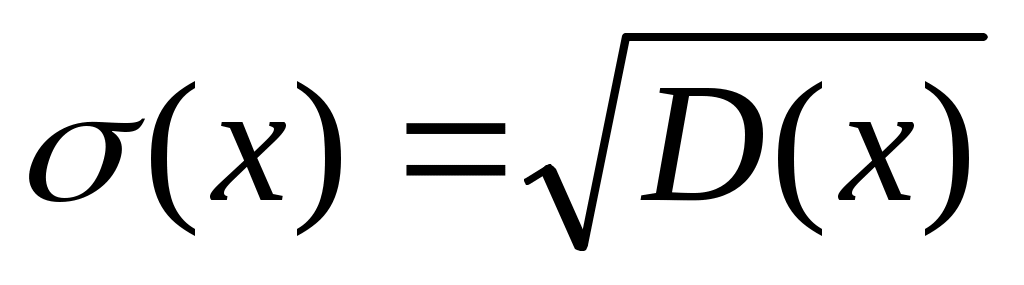 . (2.31)
. (2.31)
7. Коэффициент вариации:
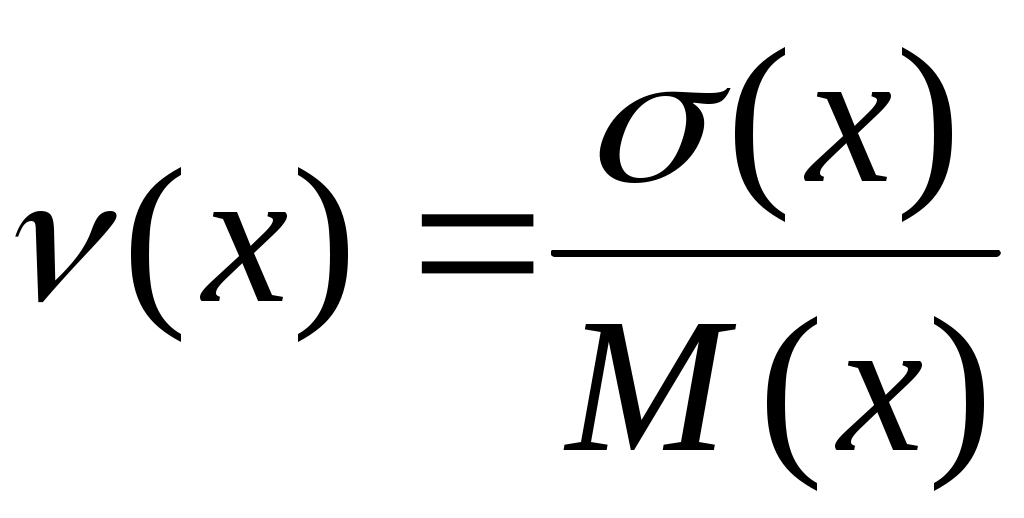 , (2.32)
, (2.32)
(х) < 0,1 – малое значение коэффициента;
(х) = 0,1…0,33 – среднее значение коэффициента;
(х) > 0,33 – большое значение коэффициента.
Свойства математического ожидания:
М(ах) = аМ(х), а= const;
М(а + х) = а + М(х);
М(х у) = М(х) М(у);
М(ху) = М(х) М(у);
М(х2) = (М(х))2 + D(х).
Свойства дисперсии:
D(ах) = а2D(х), а = const;
D(а + х) = D(х);
D(х у) = D(х) D(у);
D(х2) = М(х4) – (М(х))2 + (х)2.
Пример 2.1. Закон распределения случайной величины задан в виде таблицы:
Определить числовые характеристики случайных величин.
Решение:
М(х) = 1 · 0,3 + 2 · 0,5 + 5 · 0,2 = 2,3
D(х) = (1 – 2,3)2· 0,3 + (2 – 2,3)2 · 0,5 + (5 – 2,3)2 · 0,2 2
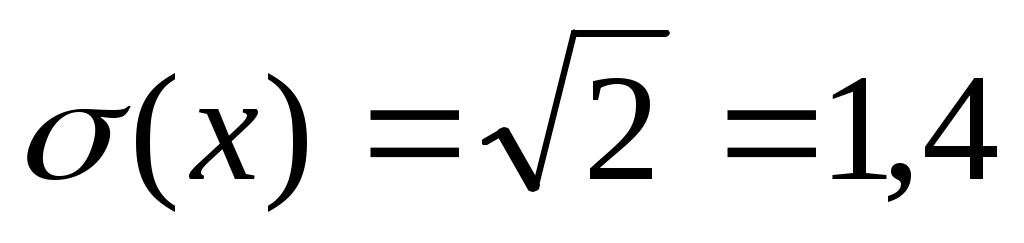
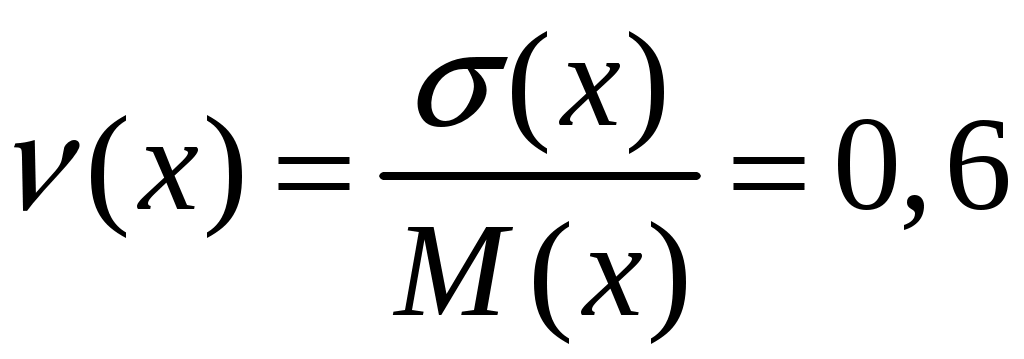 .
.
Пример 2.2. Функция распределения имеет вид:
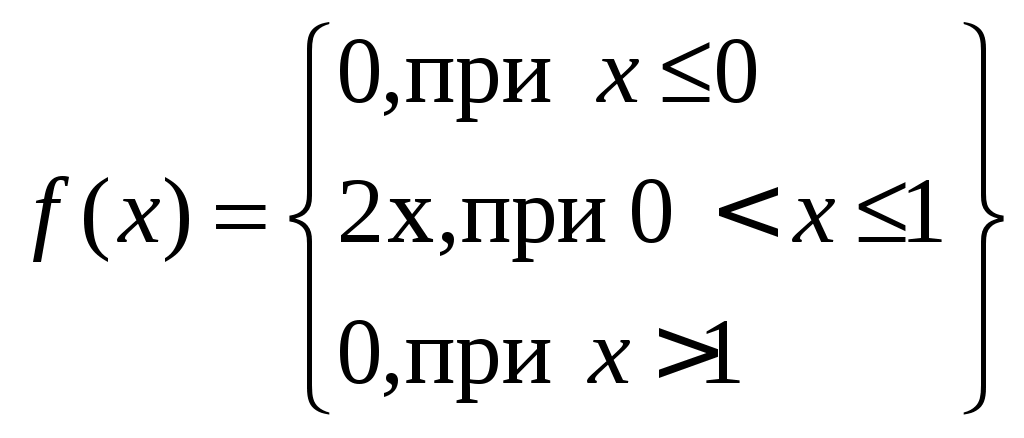
Оценить количественно, что вероятность примет значение из диапазона (0,5; 1). Какова вероятность попадания случайной величины в диапазон (0,5; 1) при условии, что событие не появится?
где
Например, вероятность отсутствия ошибки чтения 32-разрядного слова в формате ЭВМ, представляющего комбинацию 0 и 1, при вероятности ошибки чтения двоичного числа p = 10–3 составляет по (2.8) при m = 0,
При больших m вычисление биномиальных коэффициентов Cnm и возведение в большие степени p и q связано со значительными трудностями, поэтому целесообразно применять упрощенные способы расчётов. Приближение,
называемое теоремой Муавра – Лапласа, используется, если npq>>1,
а |m – np|<(npq)0,5, в таком случае выражение (2.19) записывается:
2.5. Формула полной вероятности
Если по результатам опыта можно сделать n исключающих друг друга предположений (гипотез) H1, H2, …, Hn, представляющих полную группу несовместных событий, то вероятность события А, которое может появиться только с одной из этих гипотез, определяется:
где
Поскольку событиеА может появиться с одной из гипотез
…,
. (2.23)
2.6. Формула Байеса (формула вероятностей гипотез)
Если до опыта вероятности гипотез H1, H2, … Hn были равны P(H1), P(H2), …,P(Hn), а в результате опыта произошло событие А, то новые (условные) вероятности гипотез вычисляются:
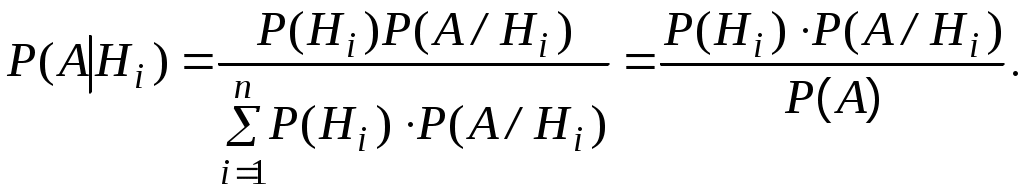 (2.24)
(2.24)Доопытные (первоначальные) вероятности гипотез P(H1), P(H2), …, P(Hn) называютсяаприорными, а послеопытные – P(H1/А), Р(Н2/А), …,
P(Hn / А) – апостериорными.
2.7. Законы распределения случайной величины
Законом распределения вероятности случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Для получения закона распределения используют три способа:
–
– для дискретных величин;
табличный (табл. 2.1)
– графический (рис. 2.1)
– аналитический – для непрерывных величин.
Таблица 2.1
Табличный закон распределения
| X | х1 | х2 | х3 | … | хn |
| P(X) | P(x1) | P(x2) | P(х3) | … | P(хn) |

Рис. 2.1. Многоугольник распределения
Для непрерывных величин табличный способ не применяется. Непрерывные случайные величины задаются функцией распределения (рис. 2.2):
F(x) = P(x1,).

Рис. 2.2. Функция распределения непрерывной случайной величины
Функция распределения имеет ряд свойств:
1) она является неубывающей функцией ее аргумента, т. е. при х2 > х1
F(х2) > F(x1);
2) на минус бесконечности функция распределения равна нулю
3) на плюс бесконечности функция распределения равна единице
Плотность распределения («плотность вероятности») – первая производная от функции распределения. Другие названия: «дифференциальная функция распределения», «дифференциальный закон распределения».
Плотность распределения изображается кривой распределения и показывает, как по оси абсцисс распределяются массы, т. е. кривая проходит через концы абсцисс значений «линейной плотности» (рис. 2.3).
Свойства плотности распределения:
1) плотность распределения – функция неотрицательная:
2) интеграл в бесконечных пределах от плотности распределения равен единице:

Рис. 2.3. Плотность распределения
Согласно свойству 2, функция распределения в интервале от 0 до х1
(рис. 2.4) определяется как интеграл плотности распределения
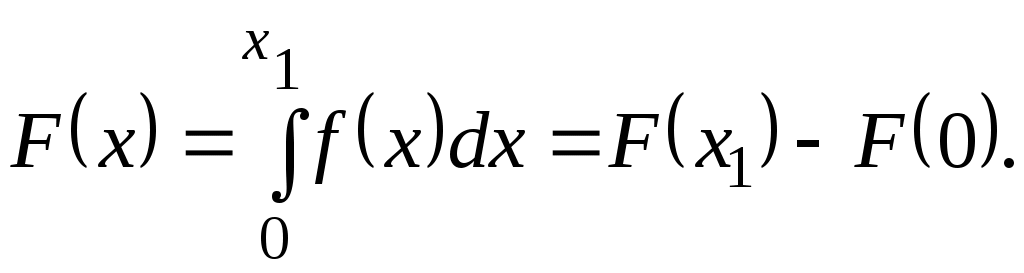 (2.26)
(2.26)Рис. 2.4. Определение функции распределения
В ряде случаев бывает достаточно указать числовые характеристики.
2.8. Числовые характеристики случайных величин
1. Математическое ожидание – характеристика центра группирования случайных величин:
– для дискретных случайных величин
– для непрерывных случайных величин
2. Модой непрерывной случайной величины называется то её значение,
в котором плотность вероятности наибольшая (т. М на рис. 2.4), М является точкой перегиба кривой.Модойдискретной случайной величины называется ее наиболее вероятное значение.
3. Медианой случайной величины Х называется такое её значение, для которого ограниченная кривой распределения площадь делится пополам (т. Ме на рис. 2.4). Площади справа и слева от медианы равны.Можно также определить медиану случайной величины X как такое ее значение Me, для которого
P(X<Me) = P(X>Me). В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.
4. Значение случайной величины, соответствующее заданной вероятности, называется квантилью. Квантиль при вероятности, равной 0,5, называется
медианой.
5. Дисперсия есть сумма произведений квадратов разностей случайных величин и математических ожиданий:
– для дискретных случайных величин
– для непрерывных случайных величин:
6. Среднее квадратическое отклонение
7. Коэффициент вариации:
(х) < 0,1 – малое значение коэффициента;
(х) = 0,1…0,33 – среднее значение коэффициента;
(х) > 0,33 – большое значение коэффициента.
Свойства математического ожидания:
М(ах) = аМ(х), а= const;
М(а + х) = а + М(х);
М(х у) = М(х) М(у);
М(ху) = М(х) М(у);
М(х2) = (М(х))2 + D(х).
Свойства дисперсии:
D(ах) = а2D(х), а = const;
D(а + х) = D(х);
D(х у) = D(х) D(у);
D(х2) = М(х4) – (М(х))2 + (х)2.
Пример 2.1. Закон распределения случайной величины задан в виде таблицы:
| х | 1 | 2 | 5 |
| Р(х) | 0,3 | 0,5 | 0,2 |
Определить числовые характеристики случайных величин.
Решение:
М(х) = 1 · 0,3 + 2 · 0,5 + 5 · 0,2 = 2,3
D(х) = (1 – 2,3)2· 0,3 + (2 – 2,3)2 · 0,5 + (5 – 2,3)2 · 0,2 2
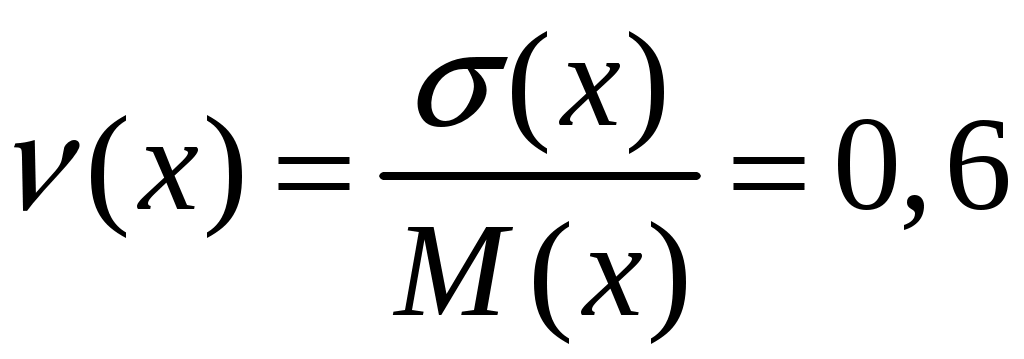 .
.Пример 2.2. Функция распределения имеет вид:
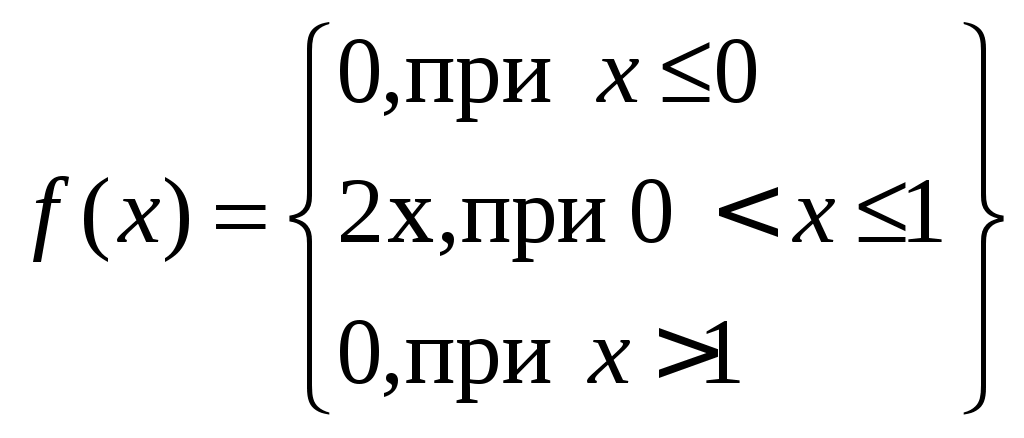
Оценить количественно, что вероятность примет значение из диапазона (0,5; 1). Какова вероятность попадания случайной величины в диапазон (0,5; 1) при условии, что событие не появится?