Файл: Учебное пособие в двух частях Часть Основы теории.doc

Контрольные вопросы

1. 
   Дайте определение понятий «вредный производственный фактор», «опас­ный производственный фактор».
   
2. 
   Влияние условий внешней среды на эффективность деятельности.
   
3. 
   Вредные и опасные факторы при работе на компьютере.
   

10.6. Применение распределения Пуассона
для оценки риска аварий

Оценка степени риска поражения людей и нанесения ущер­ба при авариях связана с задачей прогнозирования показате­лей надежности и остаточного ресурса функционирующей сис­темы. Наиболее важным вопросом является установление допустимых сроков дальнейшей эксплуатации индивидуального объекта при конкретном значении риска аварии. Ответствен­ность за соответствующие инженерные решения о мерах по снижению риска или о приостановке функционирования объ­екта лежит на комиссии, в состав которой должны входить специалисты-эксперты и представители административных ор­ганов.

Одним из основных показателей надежности объекта явля­ется вероятность P(t) безотказной работы на некотором вре­менном интервале (функция надежности). Функция Q(t) =1 – P(t), дополняющаяP(t) до единицы и характеризующая вероятность отказа, является функцией риска аварии – поражения людей и нанесения материального ущерба.

Для оценки риска применяют модели теории на­дежности. Среди них модели высоконадежных систем, для которых аварийные ситуации явление редкое, а также модели стареющих систем, качество которых в процессе эксплуатации ухудшается вследствие ползучести, различных видов усталости, износа и других видов повреждений.

Прогнозирование аварийных ситуаций возможно на основе элементарной статистики и дискретного распределения Пуассона, часто применяемого к редким событиям и природным явлениям.

Функцией риска аварии из-за отказа нормального функционирования объекта называют вероятность отказа:

H(t) = 1 – P'(t), P'(t) = exp (–∫ λ(ξ) dξ), (10.1)

λ(t) = – P'(t) / P(t),

где Р(t) – вероятность безотказной работы (функция надежно­сти); λ(t) – интенсивность отказов, равная вероятности того, что после безотказной работы до момента времени tавария произойдет в последующем малом отрезке времени.

---

Опыт показывает, что после небольшого начального периода эксплуатации (приработки) функция λ(t) длительный период достаточно стабильна, т. е. λ(t) = const. Влияние интенсивного старения за счет коррозионного износа, усталости и других факторов должно исключаться регламентированием допусти­мого срока службы.

Принимая для периода нормального (спокойного) функцио­нирования
λ(t) = const, из (10.1) получают экспоненциальное распределение

P(t) = exp(–λτ), (10.2)

причем θ = 1/λ – математическое ожидание срока службы (ресурса) или средняя наработка на отказ. Функцию риска те­перь можно записать в виде

H(t) = 1 – exp(– t/θ).(10.3)

При функции надежности в виде (10.2) частота отказов в системе однотипных объектов (поток случайных событий) со­ответствует дискретному распределению Пуассона

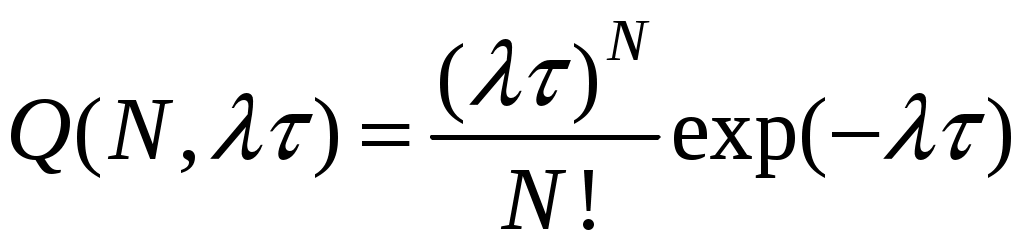, N= 0,1,2,…λτ> 0 . (10.4)

Согласно данной формуле, аварии на временном интервале τ(t, t + τ) произойдут Nраз с вероятностью Q(N, λτ), а от­сутствие аварийных ситуаций (отсутствие отказов) – с вероятностью

Q(0,λτ) = exp(– λτ).(10.5)

Вероятность того, что аварии произойдут n разпри n < N (т. е. менее
N раз), определяется функцией распределения

Q₀(n<N)= 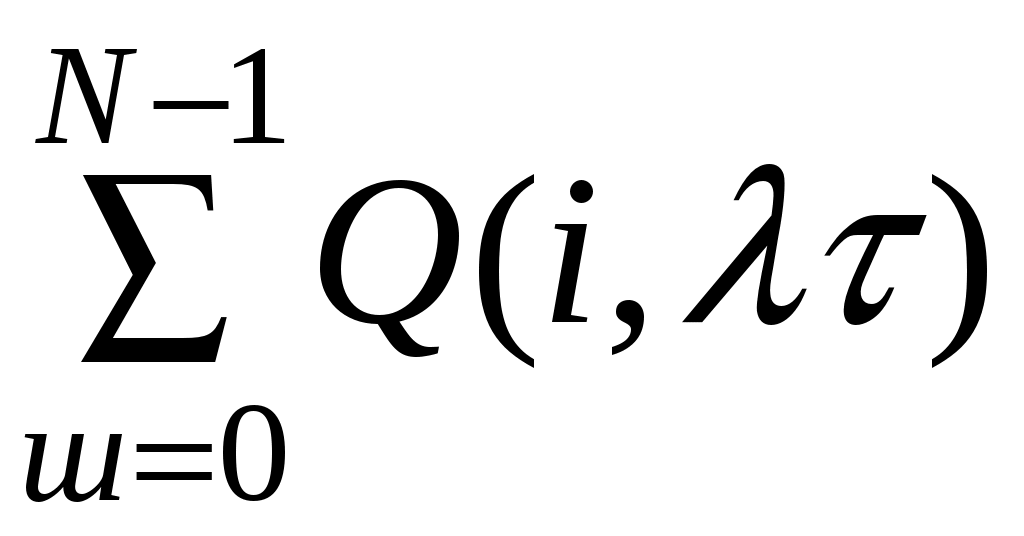=1 – φ(N,λτ) (10.6)

φ(N,λτ)=Q₀(n≥N)= .

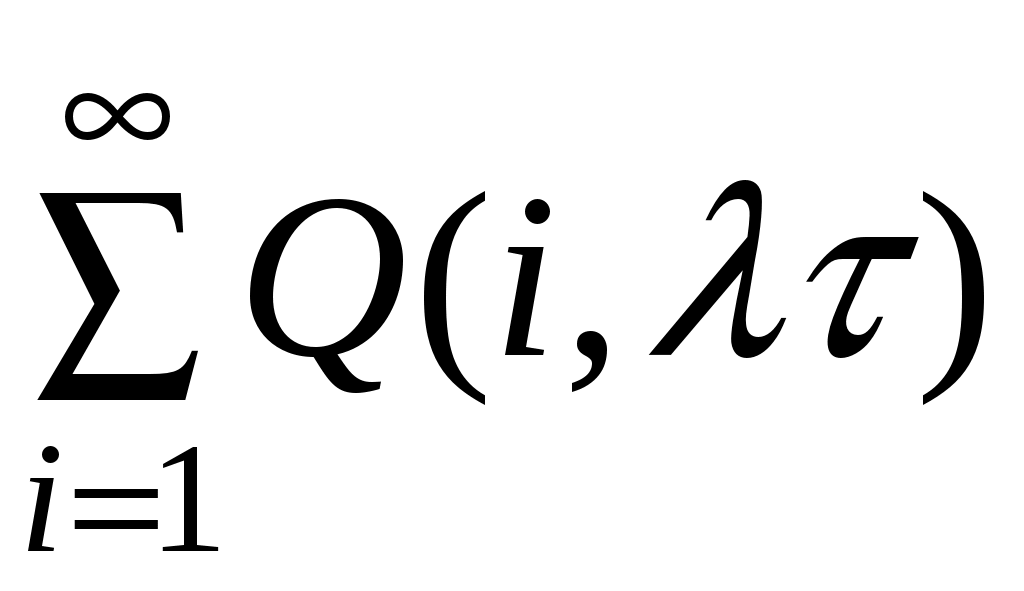Вероятность возникновения хотя бы одной аварии пред­ставляет оценку риска аварий на объекте в период τ

= 1– Q(0, λτ) = 1 – exp(–λτ) . (10.7)

Для математического ожидания Ν, дисперсии D и стандар­та σ (среднеквадратического отклонения) имеет место равен­ство N = D = σ²= λτ, т. е. имеется возможность экспериментальной проверки правдоподобия гипотезы о применимости закона Пуассона к конкретному виду аварии по факту хотя бы приблизительного соблюдения равенства

---

N = D.

Таким образом, прогнозирование аварийных ситуаций воз­можно на основе элементарной статистики. Такого рода дан­ные представляют интерес при принятии решений о мерах по снижению степени риска аварий на объектах.
Значения вероятности аварий Q(N, λτ) для числа N≤ 5 и риска возможной аварии приведены в табл. 10.3 и на рис. 10.1.
Таблица 10.3

^{Вероятность N аварий и оценка риска аварийности
в зависимости от параметра τ, согласно распределению Пуассона}

N	0,1	0,2	0,3	0,5	1,0	2,0	3,0	4,0	5,0
0	0,905	0,819	0,741	0,607	0,368	0,135	0,050	0,018	0,007
1	0,091	0,164	0,222	0,303	0,368
2	0,0045	0,016	0,033	0,076	0,184	0,271
3	0,0002	0,0011	0,0033	0,013	0,061	0,180	0,224
4		0,0001	0,0003	0,0016	0,015	0,090	0, 168	0,195
5				0,0002	0,003	0,036	0,101	0,156	0,176
	0,095	0,181	0,259	0,393	0.632	0,865	0,950	0,982	0,993

---

Закон Пуассона является частным (предельным) случаем биномиального распределения при большом числе маловероят­ных событий. В связи с этим формулу Пуассона называют законом редких явлений. На рис. 10.2 показано распределение Пуассона для нескольких значений λτ, из которого видно, что при больших значениях λτ (λτ  10) распределение приближа­ется к нормальному распределению при μ = σ² = λτ

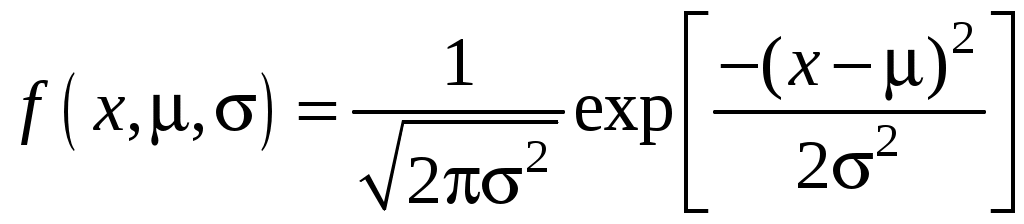. (10.8)

Закон Пуассона широко используют на практике: в теории надежности, при проверке качест­ва, при прогнозировании сейсмического риска и др. Закон Пу­ассона применим также к событиям (авариям), разбросанным на площадях. В этом случае параметр λ имеет смысл средней плотности, отнесенной не к временному интервалу, а к неко­торой площади.

1,0	Q
0,8
0,6
0,4		2	3
0,2	N=1
0	1	2	3	4	5 λτ

Рис. 10.1. Вероятность аварий и оценка риска аварийности
в зависимости от параметра λτ



0,6 Q 0,3 Q

λτ = 0,5 λτ = 1

^{0 2 4 N 0 3 6 N}

---

0,2 Q λτ = 2 0,15 Q λτ = 4
0 3 6 N 0 5 10 N

0 ,12 Q λτ = 8 0,1 Q λτ =10

0 10 20 N 0 10 20 N
Рис. 10.2. Распределение Пуассона для шести значений λτ

Известен пример исключитель­но хорошего согласия с распределением Пуассона реальной статистики падений самолетов-снарядов в южной части Лон­дона в период Второй мировой войны. Такое согласие установ­лено при подсчете числа kпадений, приходящихся на каждый из Ν = 576 одинаковых участков территории, каждый площадью S = 0,25 км². При общем числе снарядов Т =537 число участков Nk, на которое приходилось по k падений (среднее число λS = Т/N–0,9323), дано в табл. 10.4 в сравнении со значениями вероятностей Р(k; 0,9323), подсчитанных по фор­муле Пуассона.
Таблица 10.4

Сравнение статистики падения самолетов-снарядов

с соответствующим распределением Пуассона

Число падений k	0	1	2	3	4	5	≥5
Число участков Νk Q(0,9323) 576 · Q(k; 0,9323)	299 0,3936 226,74	211 0,3670 211,39	93 0,1711 98,54	35 0,0532 30,62	7 0,0124 7,14	– 0,0023 1,33	1 – –

Оценку надежности производственных установок и различ­ной аппаратуры, а также обслуживания персоналом можно провести с использованием биномиального распределения подсчетом вероятности частоты rуспешных событий (на­пример, пусков и т. п.) при их общем числе п. Доверительный интервал для фактической вероятности Р_Tопределяется урав­нением

,

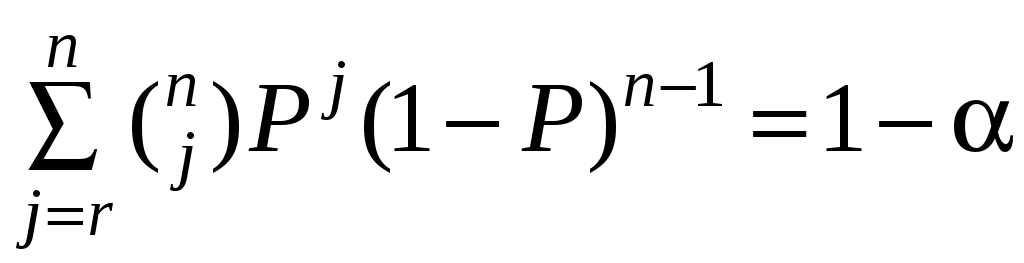где – биномиальные коэффициенты; Р – нижняя граница искомой надежности Р_Т;α – достоверность то­го, что фактическая вероятность

---