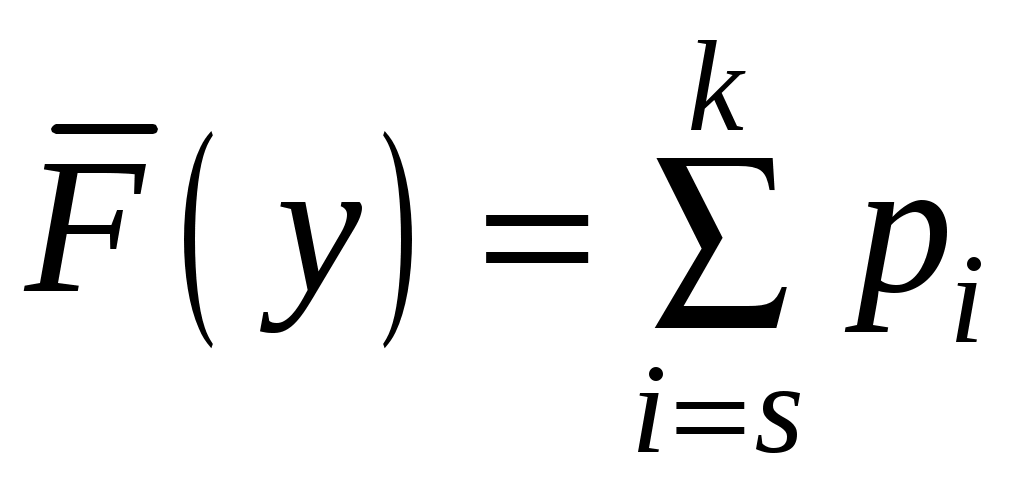ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 952
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
РТнаходится в интервале Р...1.
Значения вероятности РТпри достоверности α = 0,8 приведены в табл. 10.5 для трех значений п.
Таблица 10.5
Вероятность успешных (безаварийных) событий с достоверностью 0,8
при различных значениях r
Рассматривается альтернативный подход с привлечением модели, учитывающей некоторые физические процессы, в предположении, что авария на взрывоопасном объекте возникает в результате накопления элементарных повреждений упри достижении некоторого предельно допустимого износа М. Процесс накопления повреждений фиксируется функцией износа η(t). Отказ наступает при условии η(t) ≥ Ми числе элементарных повреждений r = М/ у.
Для объектов с высокой однородностью начального качества (обеспечивается жестким контролем качества материалов и технологии производства, что обычно реализуется при изготовлении труб, сосудов, резервуаров и газгольдеров) расчет вероятности отказа (аварии) возможен с использованием модели монотонно стареющих систем, т. е. с накапливающимися повреждениями,
на основе гамма-распределения времени Тфункционирования
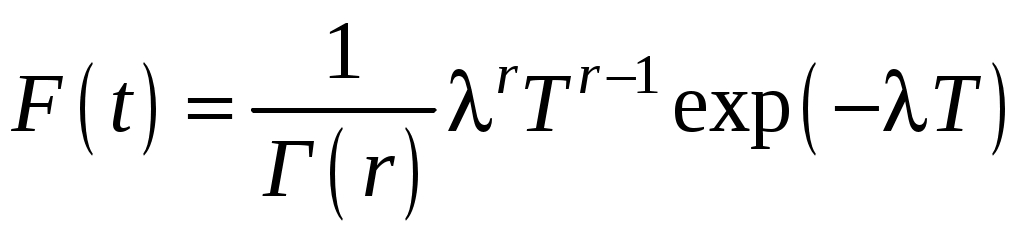 ,
,
где Г(r) – гамма-функция;λ = y–1dM·[η(t)]/dt – скорость износа.
Для целых значений rгамма-функция Г(r) = (г – 1)!, а функция распределения имеет вид
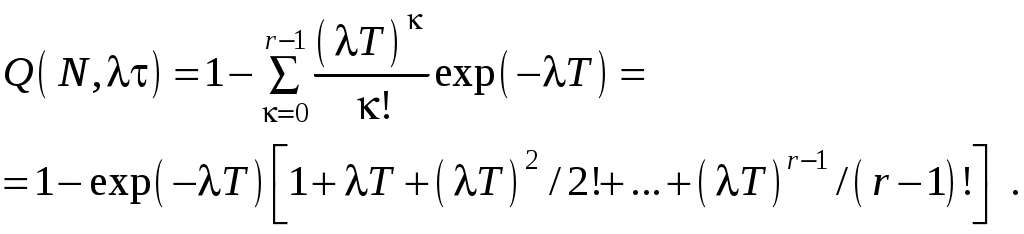
(10.9)
При r = 1 выражение (10.9) соответствует плотности экспоненциального распределения (мгновенный выход из строя при однократном повреждении).
10.7. Примеры оценки риска аварий
Пример 10.1. На объекте за 20 лет произошло 4 аварии, т. е. среднее число аварий равно λ = 4 / 20 = 0,2 лет–1. Тогда за период τ = 2 года две аварии
(N = 2) могут произойти с вероятностью Q[(2; 0,2 · 2)] = 0,42 exp(–0,4)/2! = 0,054,
а одна авария – с вероятностью Q(1; 0,4) = 0,227.
Вероятность безаварийного функционирования объекта Q(0; λτ) в течение двух лет равна Q(0; 0,4) = ехр(–0,4) = 0,67, а в течение одного года Q(0;0,2) =
= ехр(–0,2) = 0,82, т. е. риск аварийных ситуаций за двухлетний период составит 1–0,67 = 0,33, а за один год – 0,18.
Пример 10.2. Средняя скорость износа агрегата с взрывоопасным энергоносителем λ = 0,02 ч–1. Предельное число элементарных повреждений τ = 6.
Агрегат функционирует 3 ч в сутки. Определим риск аварий в течение недели.
За указанный срок время работы агрегата Т= 7 · 3 = 21 ч, λТ = 0,42.
По формуле (10.9) оценка величины риска:
R(0,42) = 1 – exp(–0,42)(1 + 0,42 + 0,422/2 + 0,423/6 + 0,424/24 + 0,425/120) =
= 5,33 ·10–6.
10.8. Примеры определения вероятности
безотказной работы технической системы
Источником техногенной ЧС на промышленном объекте, как правило, бывает отказ технической системы или элемента системы, конструктивные ошибки.
Обычно неработоспособным называют состояние объекта, при котором нельзя эксплуатировать объект. Следует считать неработоспособным объект, когда он не может выполнять своё назначение по соображениям безопасности (например, обрыв одной пряди троса).
Количественный анализ риска включает в себя оценку многочисленных факторов, однако основой или началом анализа стоит считать количественную оценку отказа системы или объекта.
Количественная оценка отказов показателями надежности не может характеризовать риск отказа промышленного объекта в полной мере. Количественный анализ отказов не учитывает влияния человеческого фактора (трудовая и технологическая дисциплина, организация управления и т. д.). При количественной оценке риска, проводимой в рамках декларирования и экспертизы промышленной безопасности опасных производственных объектов (ОПО), важно соблюдать единство подходов при использовании основных показателей риска аварии. Итоги декларирования промышленной безопасности ОПО показывают, что результаты анализа риска аварии представляются не всегда достаточно четко и определенно.
Пример 10.3. Выполняется количественная оценка аварии на ОПО. Аварии на ОПО обычно анализируют, рассматривая случайную величину потерь (ущербов) Y ≥ 0. потери Yразделяют на материальные – G (непрерывная случайная величина) и людские – N (дискретная случайная величина).
дискретная случайная величина людских потерь N при аварии на ОПО может иметь значения 0, п1, п2,..., пk. Каждому из значений величины N соответствует некоторая вероятность p0, p1, р2, …,pk.
Закон распределенияслучайной величины записан в виде таблицы:
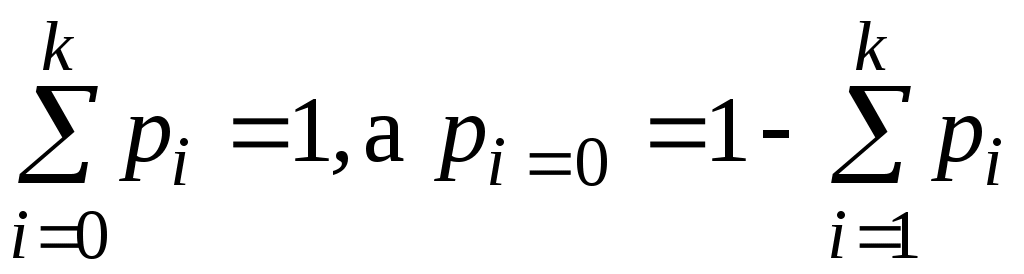 есть вероятность безаварийной эксплуатации ОПО.
есть вероятность безаварийной эксплуатации ОПО.
Исходные данные изображаются в виде многоугольника распределения. Пример многоугольника случайной величины Nдля типичного ОПО представлен на рис. 10.3.
Непрерывные случайные величины задаются функцией распределенияF(y),равной вероятности Ртого, что случайная величина Yпримет значение меньше у:
F(y) = P(Yy). (10.10)
В практике анализа риска чаще используют характеристику случайной величины потерь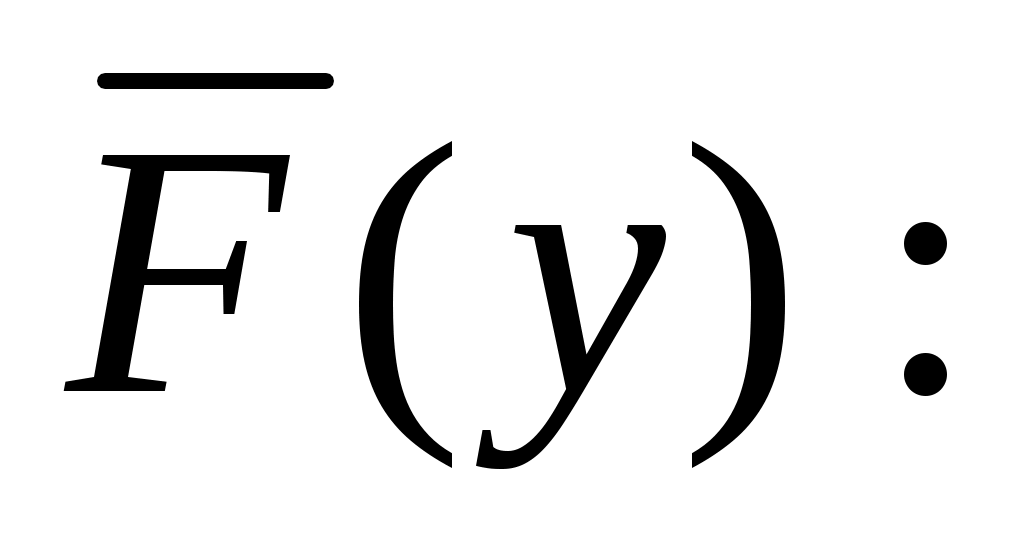
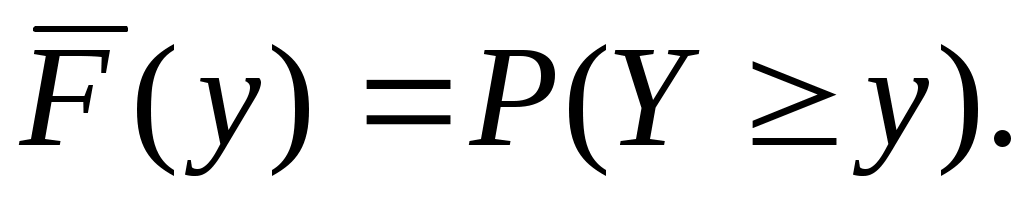 (10.11)
(10.11)
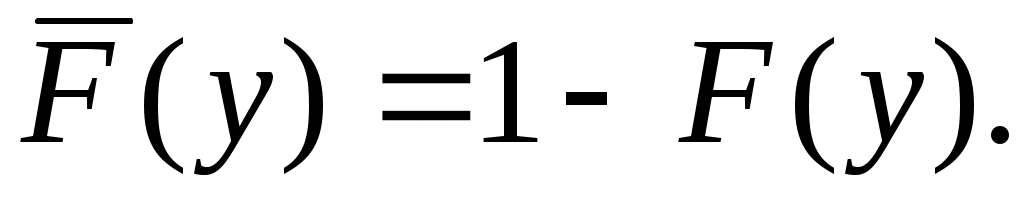 (10.12)
(10.12)
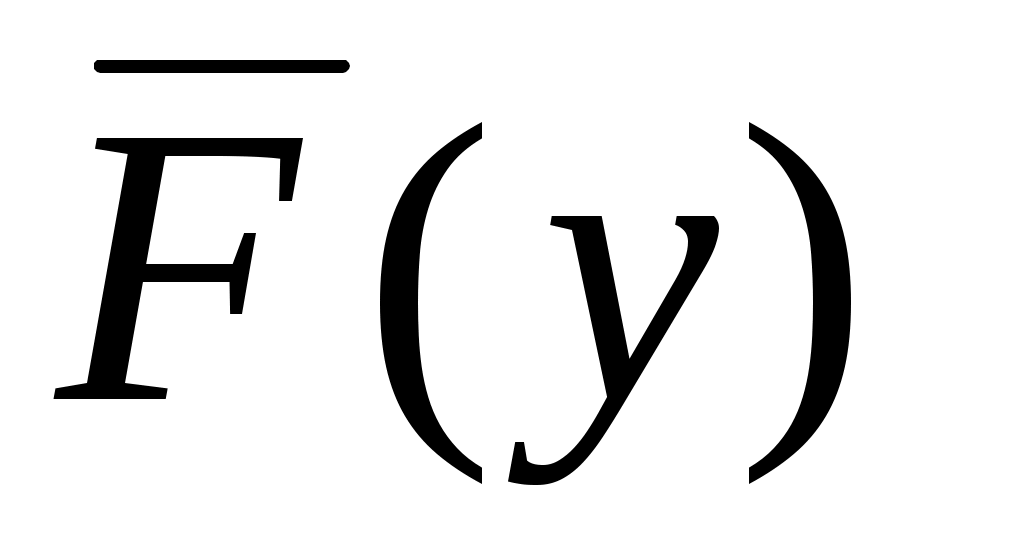 – интегральная функция распределения потерь при аварии на ОПО (F/Y – кривая). Пример графического изображения интегральной функции распределения потерь персонала при аварии
– интегральная функция распределения потерь при аварии на ОПО (F/Y – кривая). Пример графического изображения интегральной функции распределения потерь персонала при аварии 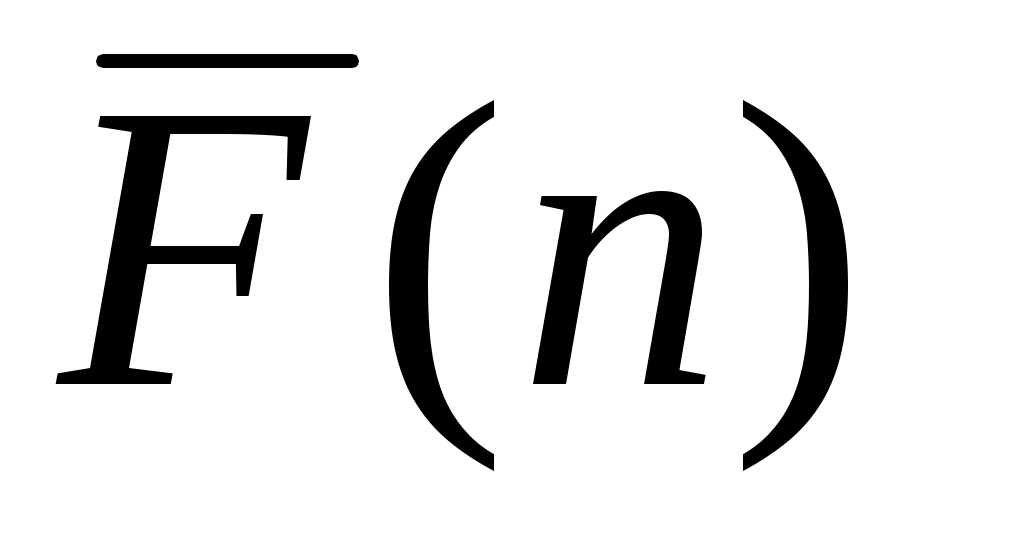 (
(
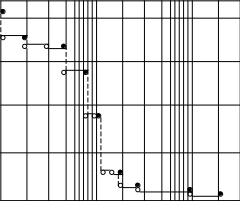
F / N – кривая) для многоугольника распределения, представленного на рис. 10.3, показан на рис. 10.4.
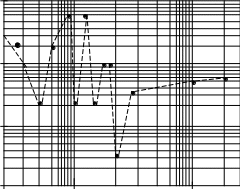 1.Е - 05
1.Е - 05
8 11
Р1 1
4 17 19
 1.Е - 06 2 20
1.Е - 06 2 20
27 100
3 10 15
1.Е - 07
21
1. Е - 08 1 10 100 ni, чел.
Рис. 10.3. Многоугольник распределения числа погибших
при аварии на нефтеперекачивающей станции с резервуарным парком
 1 - F(n)
1 - F(n)
2.0E - 05
1.5E - 05
1.0E - 05
5.1E- 05
1.0E- 07
1 10 100 n, чел.
Рис. 10.4. Интегральная функция распределения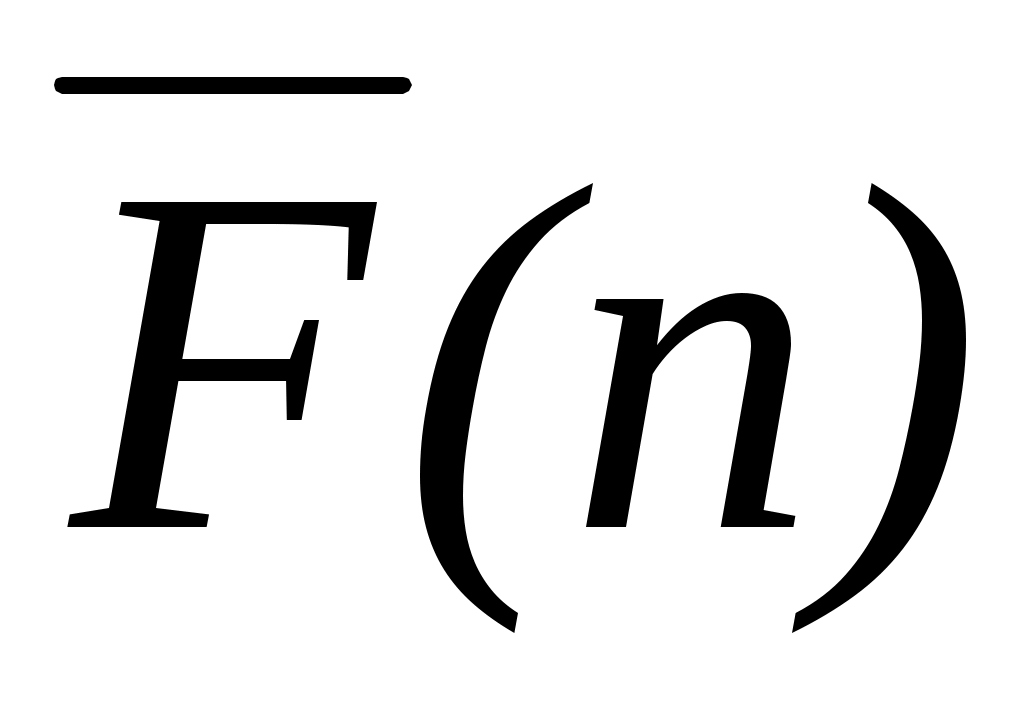 числа погибших при аварии
числа погибших при аварии
на нефтеперекачивающей станции с резервуарным парком (F/N-кривая).
В зависимости от вида потерь – людских или материальных – ее называют
F/N-кривой (диаграммой) или F/G-кривой
основные свойства интегральной функции распределения потерь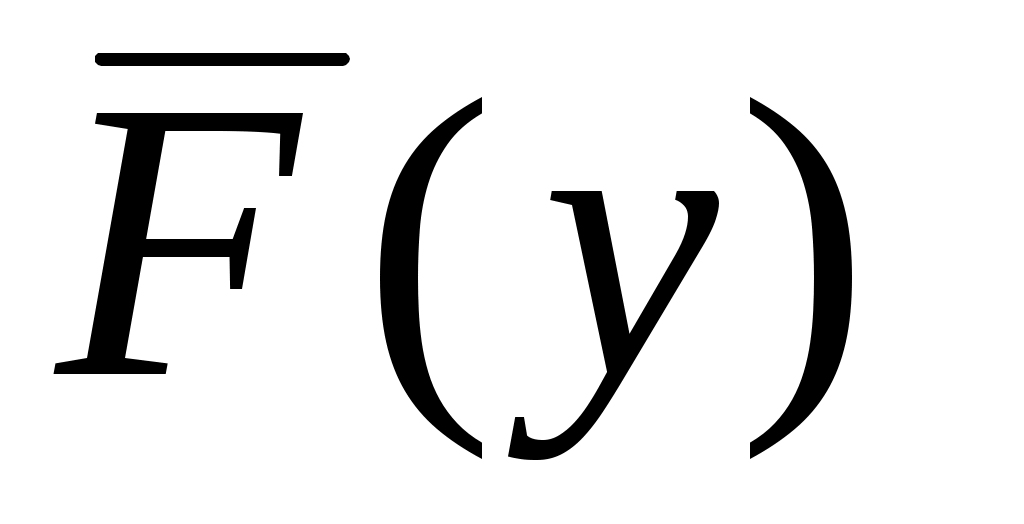 следующие:
следующие:
1.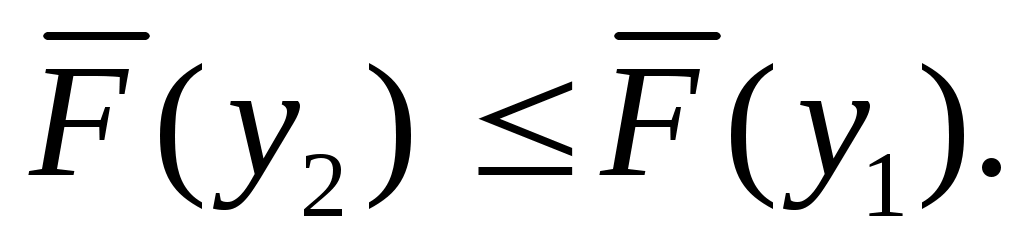
Интегральная функция распределения потерь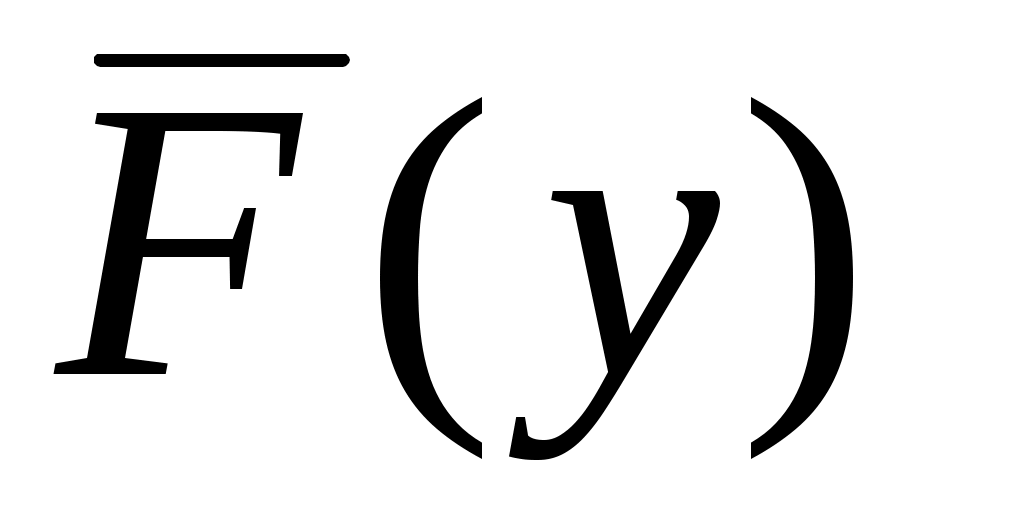 есть невозрастающая функция с неотрицательной областью определения своего аргумента у [0, +), т. е. при у2 > у1.
есть невозрастающая функция с неотрицательной областью определения своего аргумента у [0, +), т. е. при у2 > у1.
На плюс бесконечности интегральная функция распределения потерь равна нулю.
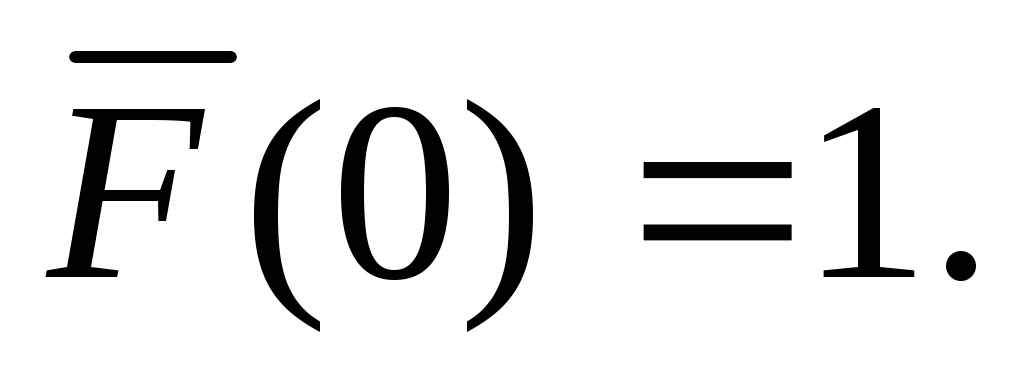
Вероятность попадания случайной величины на заданный участок
Y < (и – границы участка) равна модулю приращения интегральной функции распределения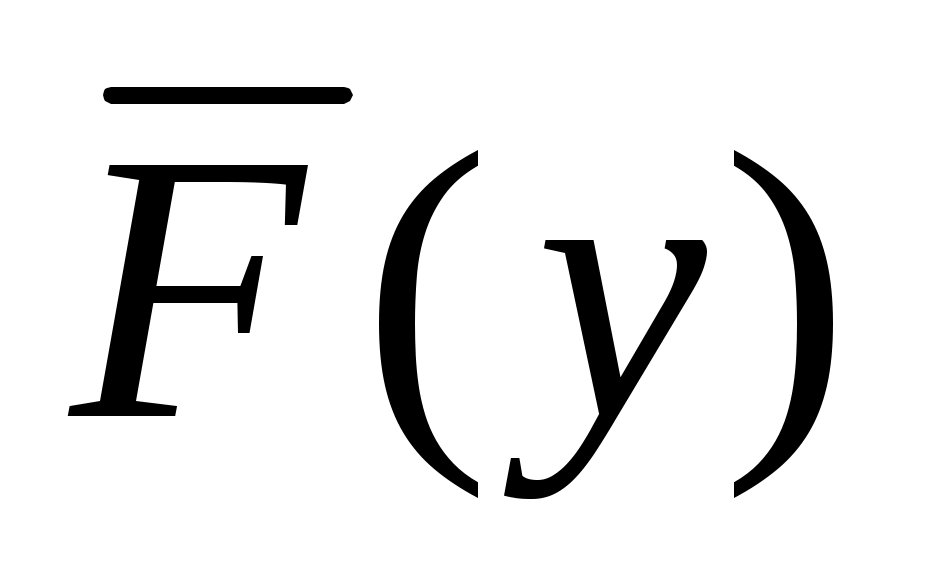 на этом участке.
на этом участке.
Приg= 1 значение интегральной функции распределения потерь нефти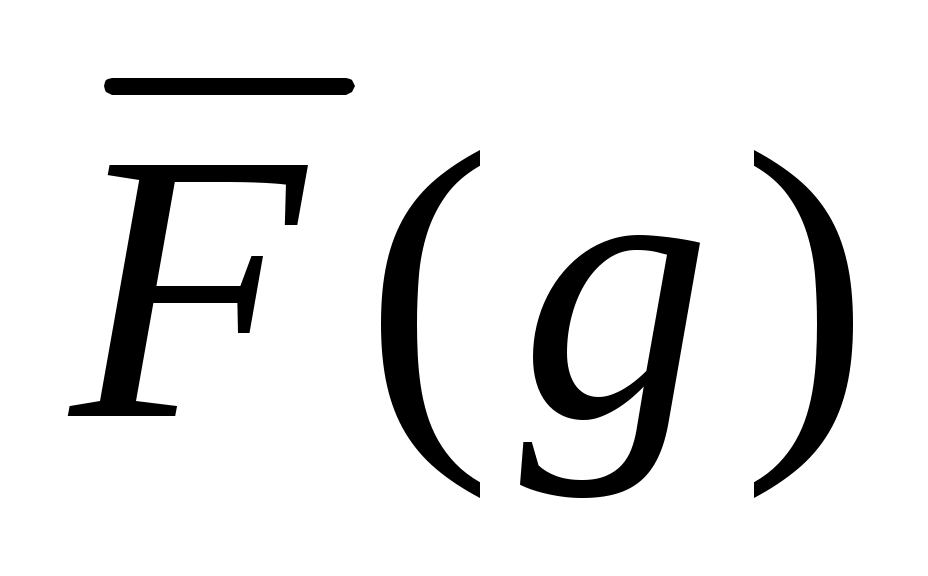 ,например, для линейной части магистральных нефтепроводов равно вероятности за год аварии с разливом более 1 т нефти. Значение F/N-кривой при n = 1 чел. равно вероятности несчастного случая со смертельным исходом, связанного с аварией на ОПО.
,например, для линейной части магистральных нефтепроводов равно вероятности за год аварии с разливом более 1 т нефти. Значение F/N-кривой при n = 1 чел. равно вероятности несчастного случая со смертельным исходом, связанного с аварией на ОПО.
Необходимо отметить, что для события «отказ технического устройства» в теории надежности, например [64], в качестве характеристики используется дискретная случайная величина Х или, в более общем случае, слуайная величина Т – момент времени наступления отказа, принимающая значения Х = 1 при наступлении отказа за определенное время или Х = 0, если отказ не наступил.
Если объектом внимания является событие, относящееся к крупным нежелательным последствиям в таких сложных системах, как банкротство компании или авария на ОПО, то анализ проводится путем рассмотрения случайной величины потерь или ущербов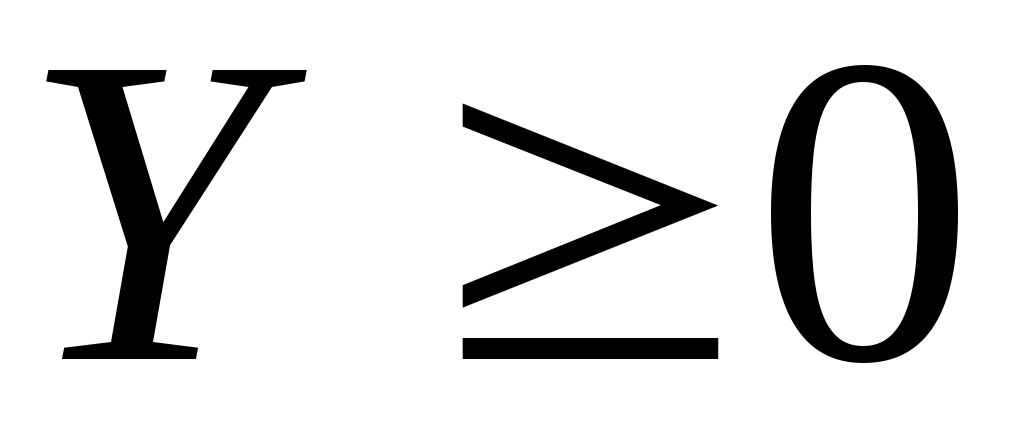 как результата деятельности. При этом в области промышленной безопасности
как результата деятельности. При этом в области промышленной безопасности 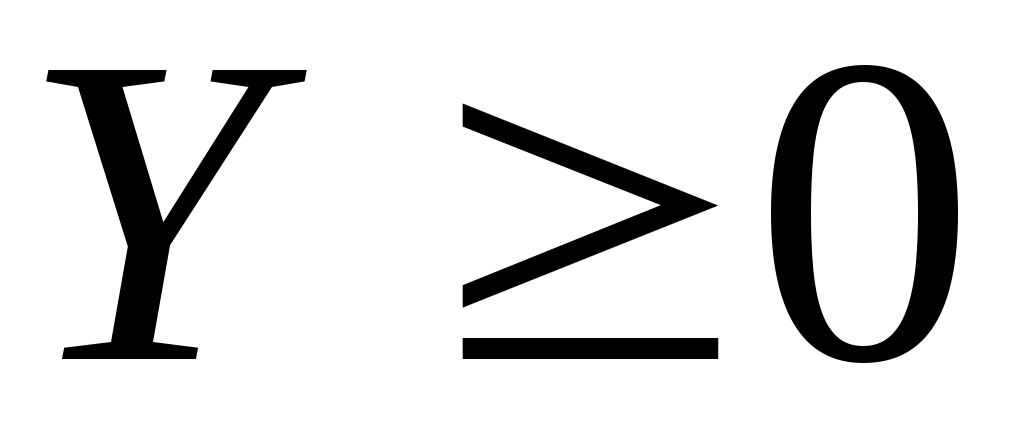 является случайной величиной потерь от аварии на ОПО, а применяемые согласно [19] определения количественных показателей риска аварии (индивидуальный, коллективный и социальный риски, ожидаемый ущерб) являются собственно характеристиками случайной величины потерь Y при аварии.
является случайной величиной потерь от аварии на ОПО, а применяемые согласно [19] определения количественных показателей риска аварии (индивидуальный, коллективный и социальный риски, ожидаемый ущерб) являются собственно характеристиками случайной величины потерь Y при аварии.
Несколько обособлено определение «потенциальный территориальный риск», характеризующее случайное событие как возникновение факторов,
достаточных для поражения человека, и оцениваемое диcкретной величиной
D= 1, если за определенное время событие происходит, и D= 0, если не происходит.
Приводится формула (10.6) в развернутом виде для более удобного построения F/N-кривых.
 1,
1,
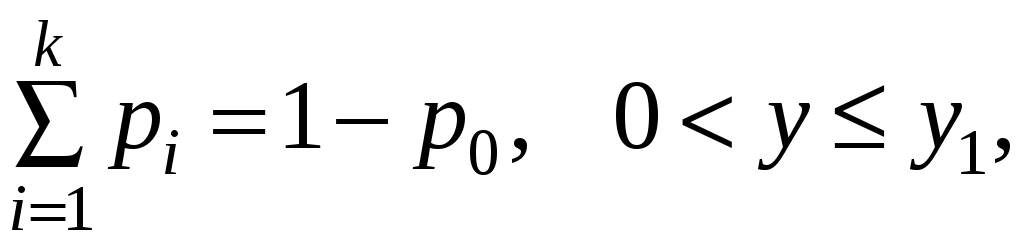
… …
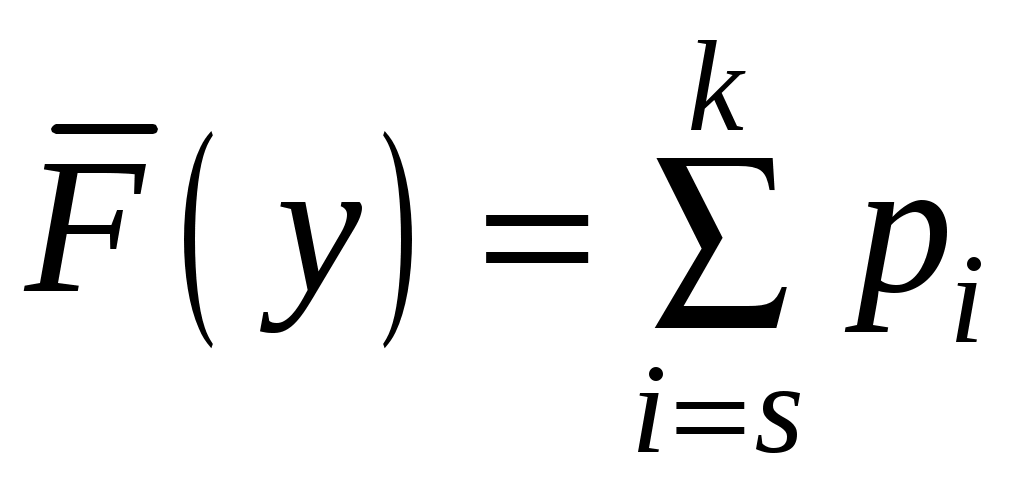
Значения вероятности РТпри достоверности α = 0,8 приведены в табл. 10.5 для трех значений п.
Таблица 10.5
Вероятность успешных (безаварийных) событий с достоверностью 0,8
при различных значениях r
| п | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 10 15 20 | 0,083 0,056 0,041 | 0,240 0,157 0,117 | 0,418 0,272 0,201 | 0,619 0,394 0,291 | 0,851 0,524 0,384 | 0,662 0,481 | 0,813 0,582 | 0,686 | 0,798 | 0,922 |
Рассматривается альтернативный подход с привлечением модели, учитывающей некоторые физические процессы, в предположении, что авария на взрывоопасном объекте возникает в результате накопления элементарных повреждений упри достижении некоторого предельно допустимого износа М. Процесс накопления повреждений фиксируется функцией износа η(t). Отказ наступает при условии η(t) ≥ Ми числе элементарных повреждений r = М/ у.
Для объектов с высокой однородностью начального качества (обеспечивается жестким контролем качества материалов и технологии производства, что обычно реализуется при изготовлении труб, сосудов, резервуаров и газгольдеров) расчет вероятности отказа (аварии) возможен с использованием модели монотонно стареющих систем, т. е. с накапливающимися повреждениями,
на основе гамма-распределения времени Тфункционирования
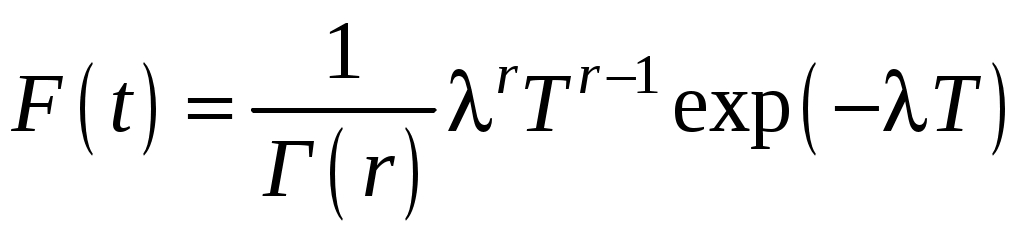 ,
,где Г(r) – гамма-функция;λ = y–1dM·[η(t)]/dt – скорость износа.
Для целых значений rгамма-функция Г(r) = (г – 1)!, а функция распределения имеет вид
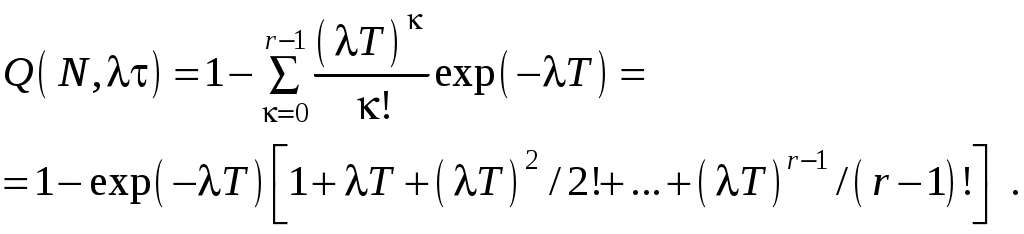
(10.9)
При r = 1 выражение (10.9) соответствует плотности экспоненциального распределения (мгновенный выход из строя при однократном повреждении).
10.7. Примеры оценки риска аварий
Пример 10.1. На объекте за 20 лет произошло 4 аварии, т. е. среднее число аварий равно λ = 4 / 20 = 0,2 лет–1. Тогда за период τ = 2 года две аварии
(N = 2) могут произойти с вероятностью Q[(2; 0,2 · 2)] = 0,42 exp(–0,4)/2! = 0,054,
а одна авария – с вероятностью Q(1; 0,4) = 0,227.
Вероятность безаварийного функционирования объекта Q(0; λτ) в течение двух лет равна Q(0; 0,4) = ехр(–0,4) = 0,67, а в течение одного года Q(0;0,2) =
= ехр(–0,2) = 0,82, т. е. риск аварийных ситуаций за двухлетний период составит 1–0,67 = 0,33, а за один год – 0,18.
Пример 10.2. Средняя скорость износа агрегата с взрывоопасным энергоносителем λ = 0,02 ч–1. Предельное число элементарных повреждений τ = 6.
Агрегат функционирует 3 ч в сутки. Определим риск аварий в течение недели.
За указанный срок время работы агрегата Т= 7 · 3 = 21 ч, λТ = 0,42.
По формуле (10.9) оценка величины риска:
R(0,42) = 1 – exp(–0,42)(1 + 0,42 + 0,422/2 + 0,423/6 + 0,424/24 + 0,425/120) =
= 5,33 ·10–6.
10.8. Примеры определения вероятности
безотказной работы технической системы
Источником техногенной ЧС на промышленном объекте, как правило, бывает отказ технической системы или элемента системы, конструктивные ошибки.
Обычно неработоспособным называют состояние объекта, при котором нельзя эксплуатировать объект. Следует считать неработоспособным объект, когда он не может выполнять своё назначение по соображениям безопасности (например, обрыв одной пряди троса).
Количественный анализ риска включает в себя оценку многочисленных факторов, однако основой или началом анализа стоит считать количественную оценку отказа системы или объекта.
Количественная оценка отказов показателями надежности не может характеризовать риск отказа промышленного объекта в полной мере. Количественный анализ отказов не учитывает влияния человеческого фактора (трудовая и технологическая дисциплина, организация управления и т. д.). При количественной оценке риска, проводимой в рамках декларирования и экспертизы промышленной безопасности опасных производственных объектов (ОПО), важно соблюдать единство подходов при использовании основных показателей риска аварии. Итоги декларирования промышленной безопасности ОПО показывают, что результаты анализа риска аварии представляются не всегда достаточно четко и определенно.
Пример 10.3. Выполняется количественная оценка аварии на ОПО. Аварии на ОПО обычно анализируют, рассматривая случайную величину потерь (ущербов) Y ≥ 0. потери Yразделяют на материальные – G (непрерывная случайная величина) и людские – N (дискретная случайная величина).
дискретная случайная величина людских потерь N при аварии на ОПО может иметь значения 0, п1, п2,..., пk. Каждому из значений величины N соответствует некоторая вероятность p0, p1, р2, …,pk.
Закон распределенияслучайной величины записан в виде таблицы:
| ni | 0 | n1 | n2 | … ns … | nk |
| Pi | | p1 | p2 | … ps … | pk |
Исходные данные изображаются в виде многоугольника распределения. Пример многоугольника случайной величины Nдля типичного ОПО представлен на рис. 10.3.
Непрерывные случайные величины задаются функцией распределенияF(y),равной вероятности Ртого, что случайная величина Yпримет значение меньше у:
F(y) = P(Yy). (10.10)
В практике анализа риска чаще используют характеристику случайной величины потерь
F / N – кривая) для многоугольника распределения, представленного на рис. 10.3, показан на рис. 10.4.
 1.Е - 05
1.Е - 058 11
Р1 1
4 17 19
 1.Е - 06 2 20
1.Е - 06 2 2027 100
3 10 15
1.Е - 07
21
1. Е - 08 1 10 100 ni, чел.
Рис. 10.3. Многоугольник распределения числа погибших
при аварии на нефтеперекачивающей станции с резервуарным парком
 1 - F(n)
1 - F(n)2.0E - 05
1.5E - 05
1.0E - 05
5.1E- 05
1.0E- 07
1 10 100 n, чел.
Рис. 10.4. Интегральная функция распределения
на нефтеперекачивающей станции с резервуарным парком (F/N-кривая).
В зависимости от вида потерь – людских или материальных – ее называют
F/N-кривой (диаграммой) или F/G-кривой
основные свойства интегральной функции распределения потерь
1.
Интегральная функция распределения потерь
На плюс бесконечности интегральная функция распределения потерь равна нулю.
-
При нулевом аргументе интегральная функция распределения потерь принимает значение, равное единице.
-
Интегральная функция распределения людских потерь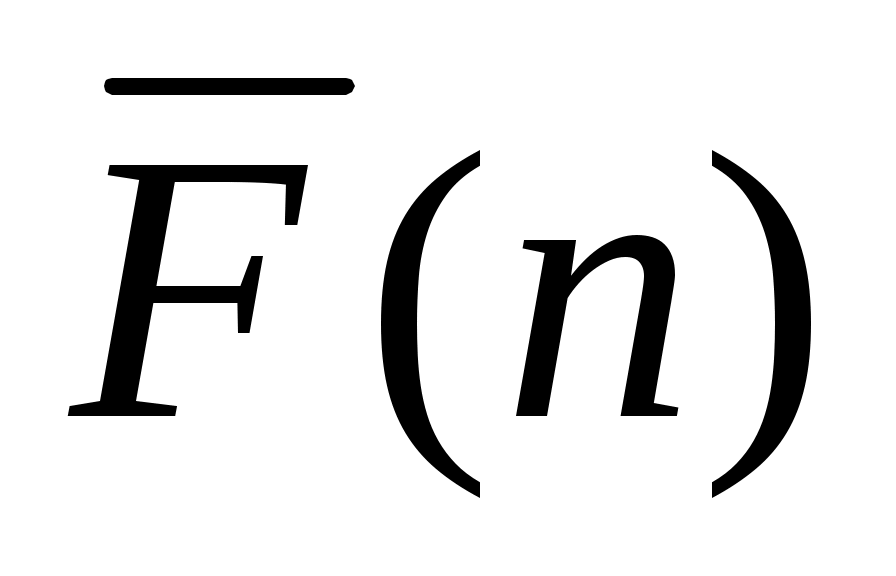 есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины N,и равны вероятностям этих значений. Сумма всех скачков
есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины N,и равны вероятностям этих значений. Сумма всех скачков 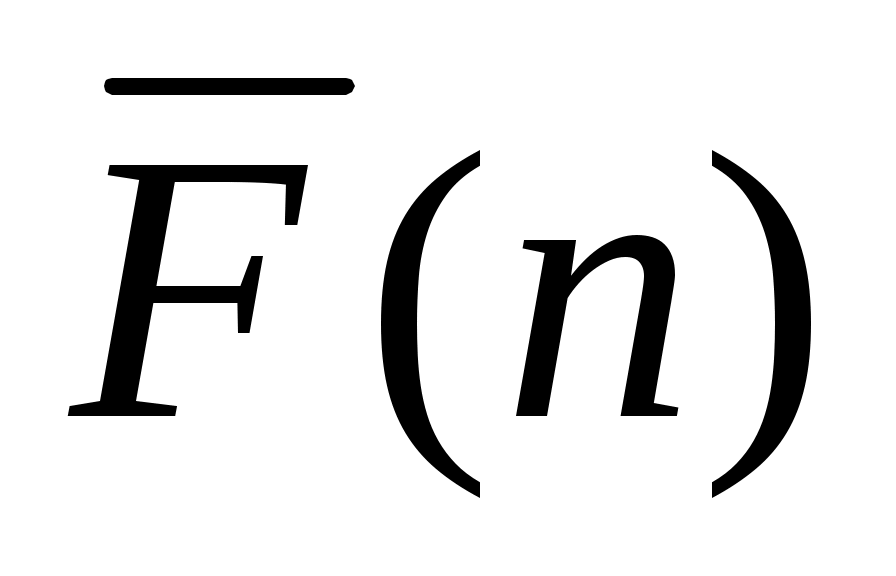 равна единице.
равна единице. -
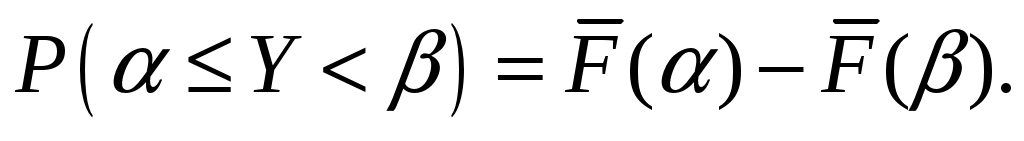
Вероятность попадания случайной величины на заданный участок
Y < (и – границы участка) равна модулю приращения интегральной функции распределения
Приg= 1 значение интегральной функции распределения потерь нефти
Необходимо отметить, что для события «отказ технического устройства» в теории надежности, например [64], в качестве характеристики используется дискретная случайная величина Х или, в более общем случае, слуайная величина Т – момент времени наступления отказа, принимающая значения Х = 1 при наступлении отказа за определенное время или Х = 0, если отказ не наступил.
Если объектом внимания является событие, относящееся к крупным нежелательным последствиям в таких сложных системах, как банкротство компании или авария на ОПО, то анализ проводится путем рассмотрения случайной величины потерь или ущербов
Несколько обособлено определение «потенциальный территориальный риск», характеризующее случайное событие как возникновение факторов,
достаточных для поражения человека, и оцениваемое диcкретной величиной
D= 1, если за определенное время событие происходит, и D= 0, если не происходит.
Приводится формула (10.6) в развернутом виде для более удобного построения F/N-кривых.
 1,
1,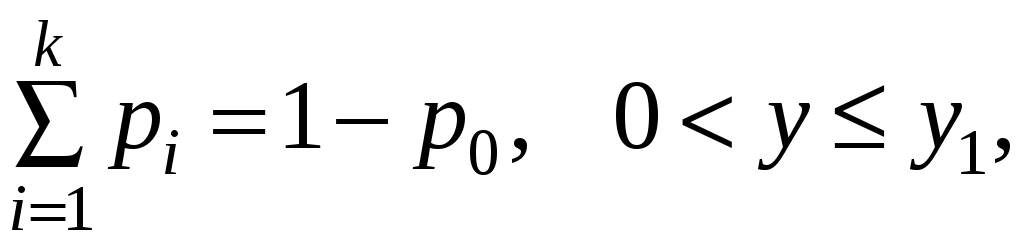
… …