Добавлен: 23.11.2023
Просмотров: 129
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
λ и z следующими соотношениями
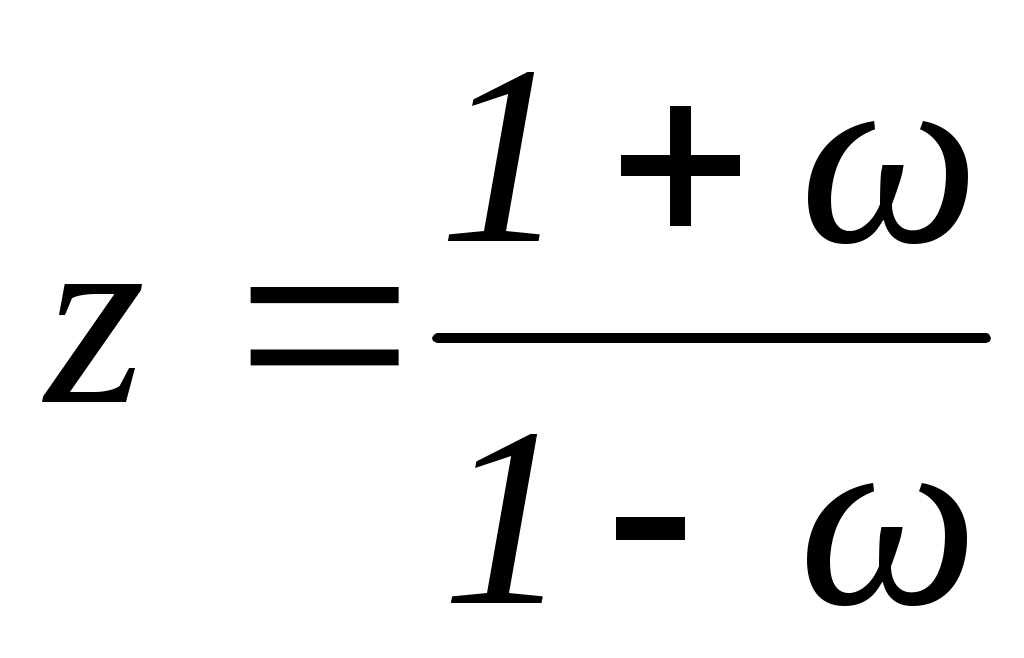 (27)
(27)
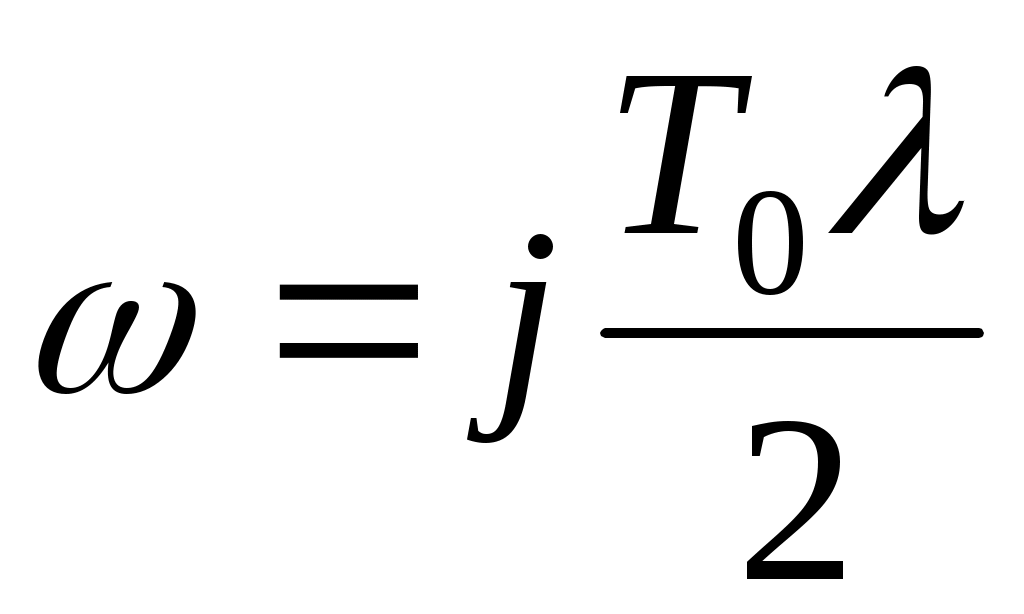 (28)
(28)
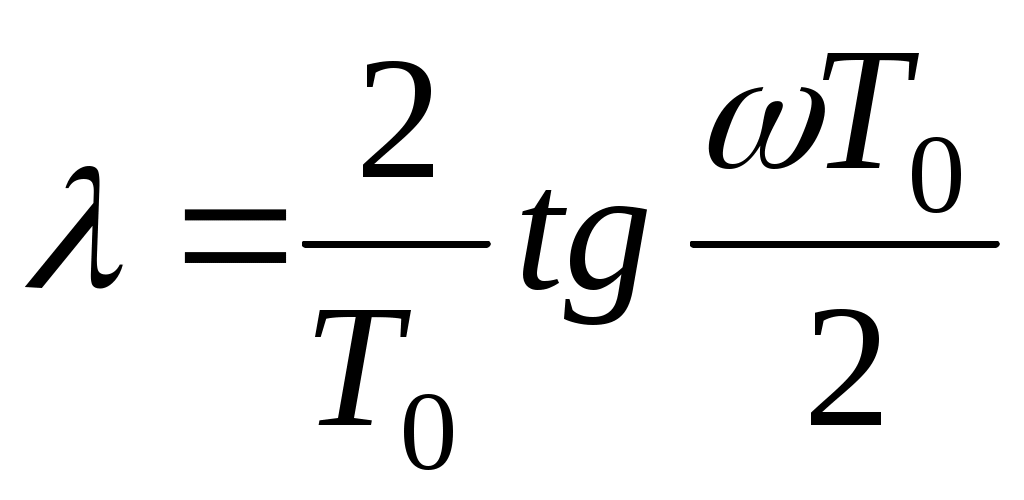 (29)
(29)
Логарифмические частотные характеристики представляют собой амплитудную и фазовую частотные характеристики САР, построенные в полулогарифмическом масштабе.
Логарифмической амплитудной частотной характеристикой (ЛАЧХ) системы называется кривая, соответствующая 20 десятичным логарифмам модуля частотной характеристики (АЧХ), построенная в десятичном логарифмическом масштабе частот:
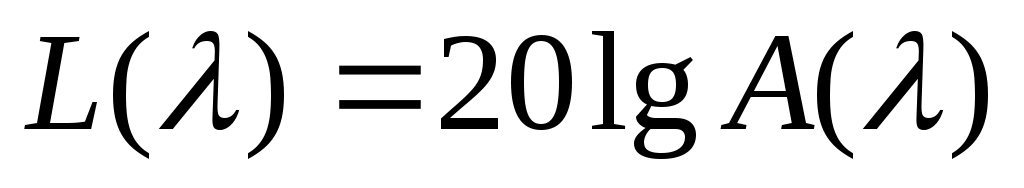 , (29)
, (29)
где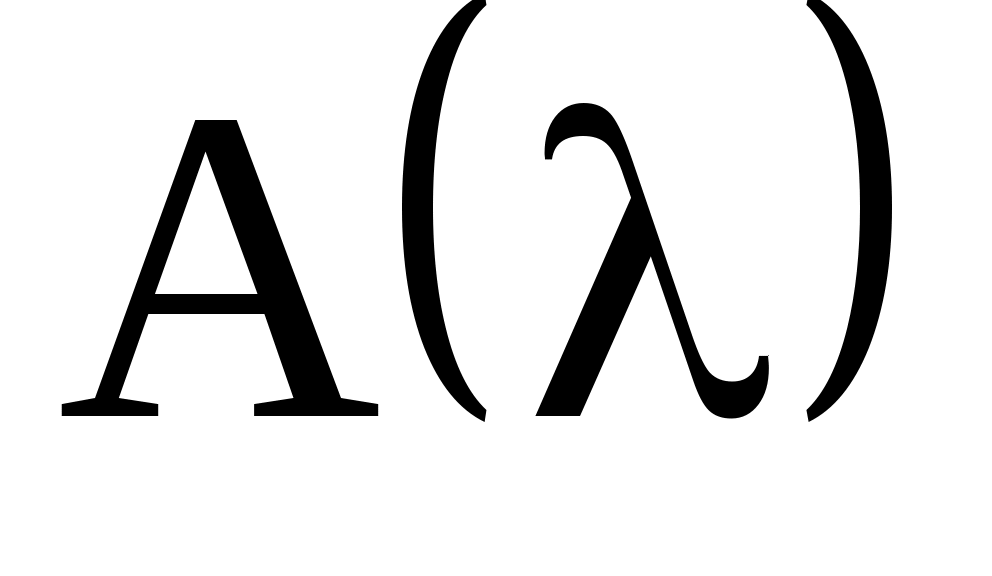 - амплитудно-частотная функция системы.
- амплитудно-частотная функция системы.
Тогда для построения ЛАЧХ можно использовать передаточную функцию непрерывной разомкнутой системы. Данное выражение представляет собой произведение коэффициента усиления и передаточных функций элементарных динамических звеньев.
Известно, что псевдочастота практически совпадает с круговой частотой в области, где выполняется условие:
T0<2Tmin, (30)
где Tmin – минимальная постоянная времени элементов разомкнутой системы.
Так как минимальная постоянная времени, соответствующая датчика положения равна 8 с., выбранный период дискретизации – 6, то неравенство выполняется всегда (6<2.8) и во всей области работы системы можно положить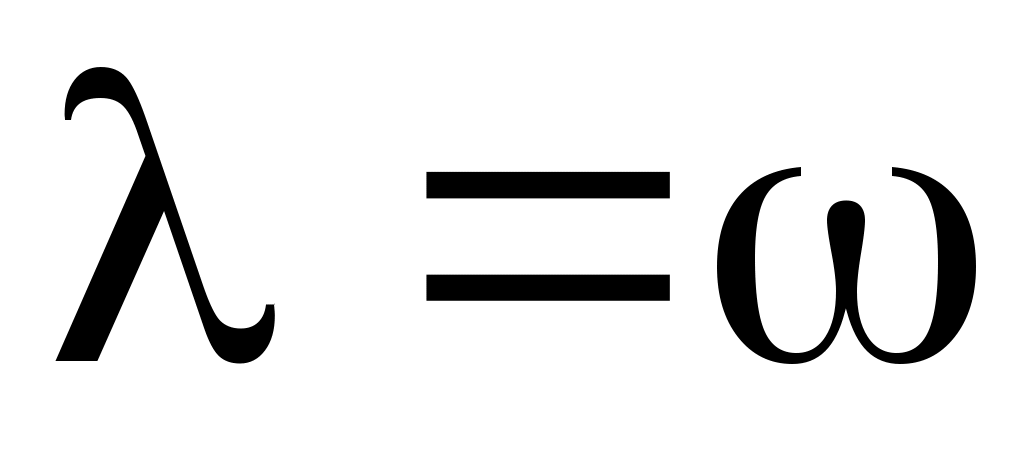 .Логарифмической фазовой частотной характеристикой (ЛФЧХ) системы называется фазовая частотная характеристика, построенная в десятичном логарифмическом масштабе частот.
.Логарифмической фазовой частотной характеристикой (ЛФЧХ) системы называется фазовая частотная характеристика, построенная в десятичном логарифмическом масштабе частот.
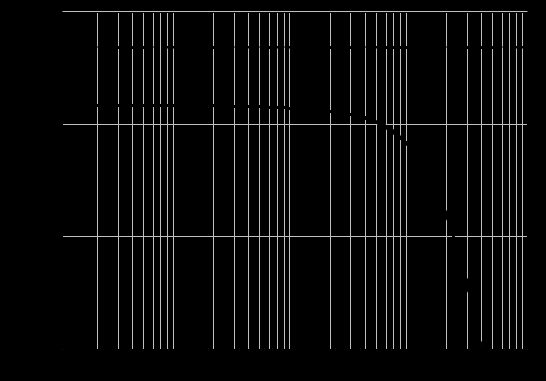


Рисунок 24 - ЛАЧХ разомкнутой системы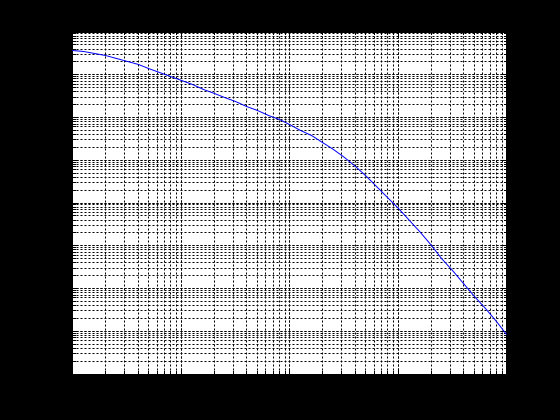
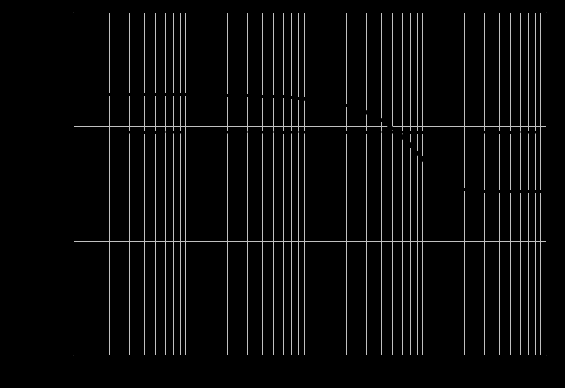

Рисунок 25 - ЛФЧХ разомкнутой системы
По построенным характеристикам определим запасы по фазе и амплитуде. Запас по амплитуде определяется следующим образом. Находится частота при которой ЛФЧХ первый раз пересекает прямую со значением -1800, в этой частоте проводится вертикальная прямая до пересечения с ЛАЧХ.
Расстояние от этой точки пересечения до оси составляет запас устойчивости по амплитуде в децибелах. В нашем случае запас по амплитуде 50 дб/дек.
Запас устойчивости по фазе определяется следующим образом. Определяется частота при которой ЛАЧХ пересекает ось (0 децибел). При этой частоте проводится вертикальная прямая вниз до пересечения с ЛФЧХ. Расстояние от точки пересечения до прямой -1800 составит запас по фазе в градусах. В нашем случае ЛАЧХ пересекает ось 0, следовательно, запас по фазе составляет 20,75°.
Так как время переходного процесса не соответствует требуемому, то системе требуется коррекция.
5.4 Анализ качества системы
5.3.1 Прямые оценки качества. Для наглядного отображения свойств рассматриваемой системы построим переходный процесс, воспользовавшись обратным преобразованием Лапласа от передаточной функции замкнутой системы.
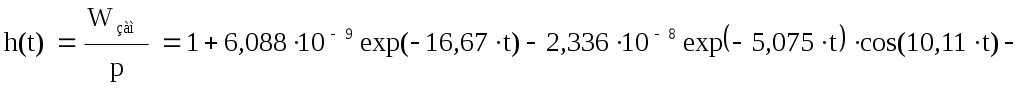 (31)
(31)
По графику переходного процесса (рисунок 24) определим прямые показатели качества системы:
а) Время регулирования (время переходного процесса) - время, за которое система приходит к установившемуся значению с некоторой долей погрешности. Обычно она составляет 5% (пятипроцентная трубка). Приблизительно время регулирования составляет 186,3 (с).
tp = 186,3с
Время первого согласования t1=325.
б) Перерегулирование отражает в процентах максимальное отклонение от установившегося значения.
Максимальное значение отсутствует, тогда перерегулирование:
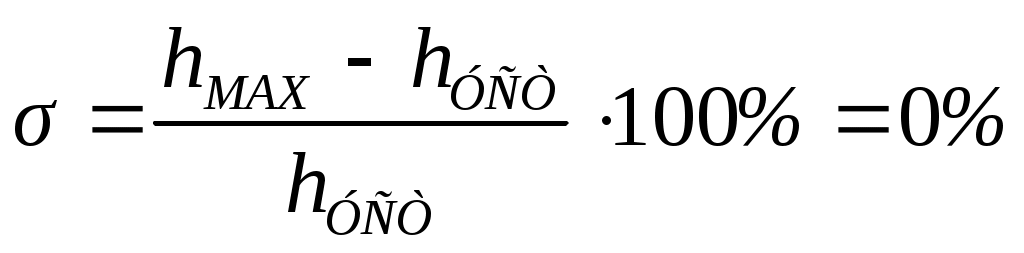 (32)
(32)


Рисунок 26– Переходный процесс нескорректированной системы
По характеру переходного процесса можно судить об устойчивости системы: характеристика устойчивая монотонно возрастающая.
5.3.2 Косвенные оценки качества. Косвенные оценки качества проводятся по частотным характеристикам. Наиболее часто используется амплитудно-частотная характеристика. (АЧХ) замкнутой системы.
Амплитудно-частотная функция определяется по формуле:
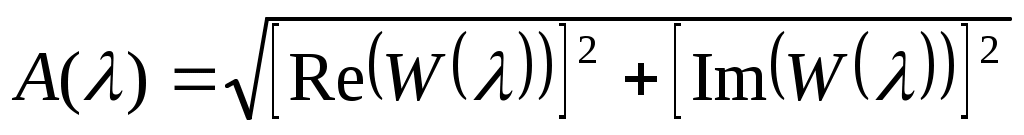 (33)
(33)
График АЧХ замкнутой системы приведен на рисунке 25.
Косвенные оценки качества:
- показатель колебательности, определяемый по формуле
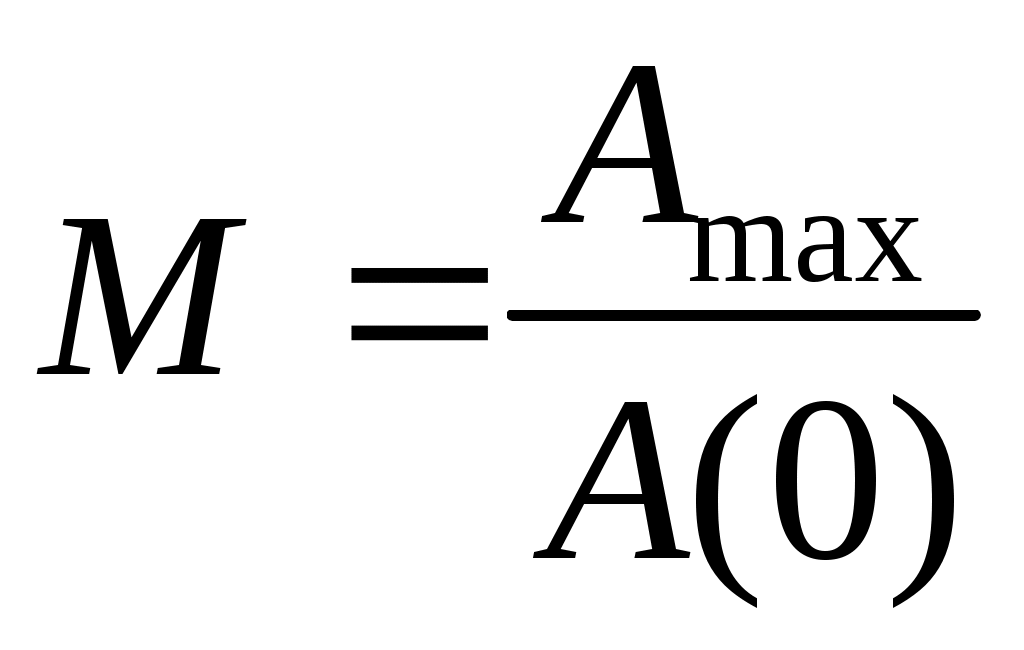 ,
,
где Amax – максимум АЧХ;
A(0) – значение амплитуды при нулевой частоте.
A(0)=0,99 рад/с
Amax=20,6
В данном случае M=21 – переходный процесс протекает с колебаниями по апериодическому закону.
Рисунок 27 – АЧХ системы
- Частота среза – частота, при которой АЧХ достигает значения, равного 1.
Частота среза косвенно характеризует быстродействие системы: чем больше часта среза, тем меньше время регулирования.
λср= 1,8 рад/с
- Резонансная частота – частота, в которой амплитудно-частотная функция достигает своего максимального значения:
λр=0,46 рад/с
- Полоса пропускания – интервал частот, в котором амплитуда АЧХ превышает уровень 0.707 Amax
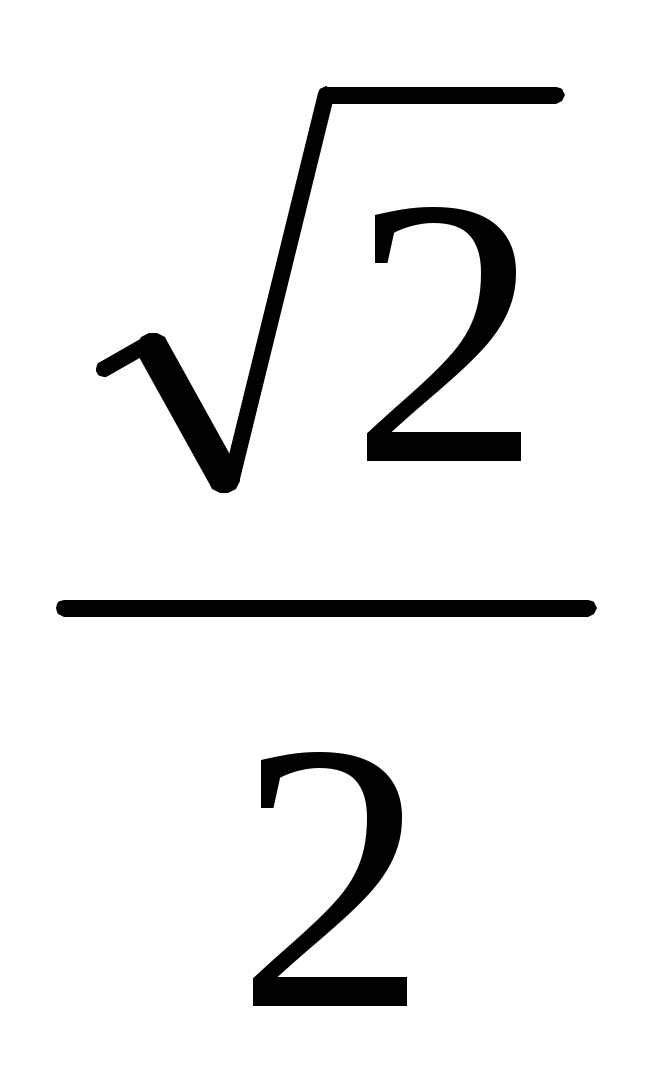 Amax=14,6
Amax=14,6
0.245<ω<0.644
5.5 Построение желаемой ЛАЧХ.
Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства. Желаемая ЛАЧХ строится на основании требований к системе, отраженных в техническом задании, при этом рекомендуется, чтобы характеристика не скорректированной системы и желаемая характеристика скорректированной системы совпадали друг с другом в возможно более широком диапазоне частот. В противном случае реализация корректирующих устройств резко усложняется.
Построим желаемую ЛАЧХ исследуемой системы, используюя метод запретной области.
Рассмотрим низкочастотную часть желаемой ЛАЧХ системы.
Отметим в низкочастотной области желаемой ЛАЧХ запретную зону для обеспечения требований по ошибке при заданных скорости и ускорении входного сигнала.
Запишем некоторые данные из технического задания для нашей системы:
Максимально допустимая ошибка
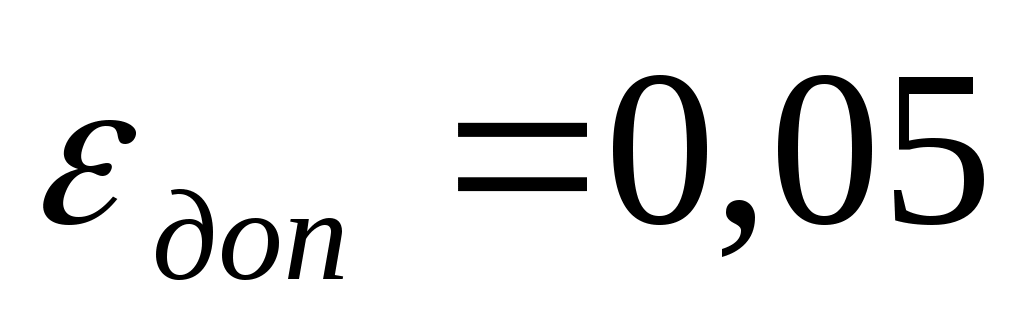
Максимальна скорость изменения pH пульпы
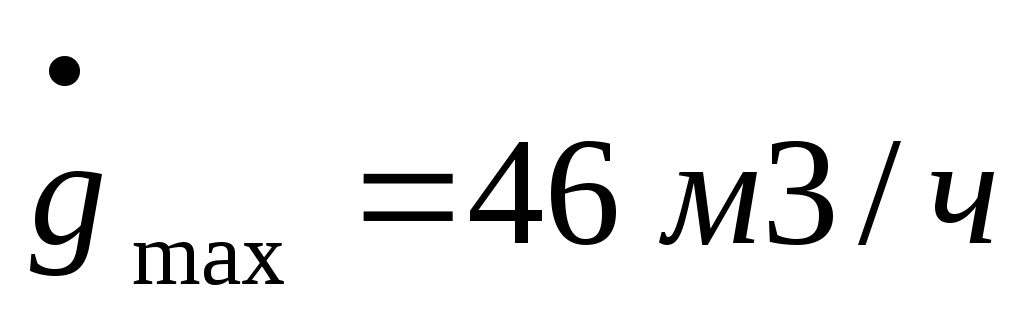
Максимальное ускорение
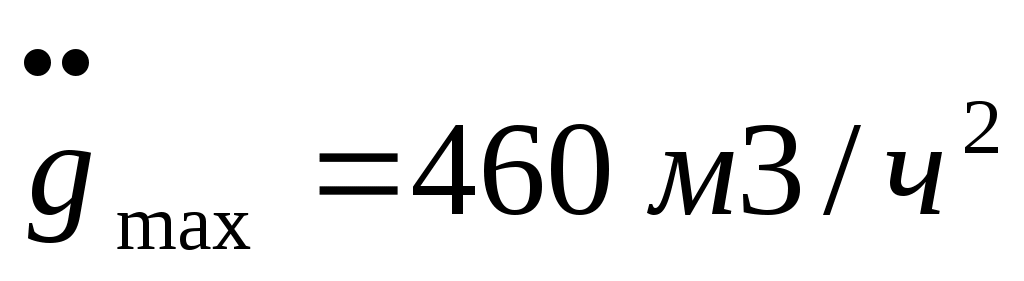
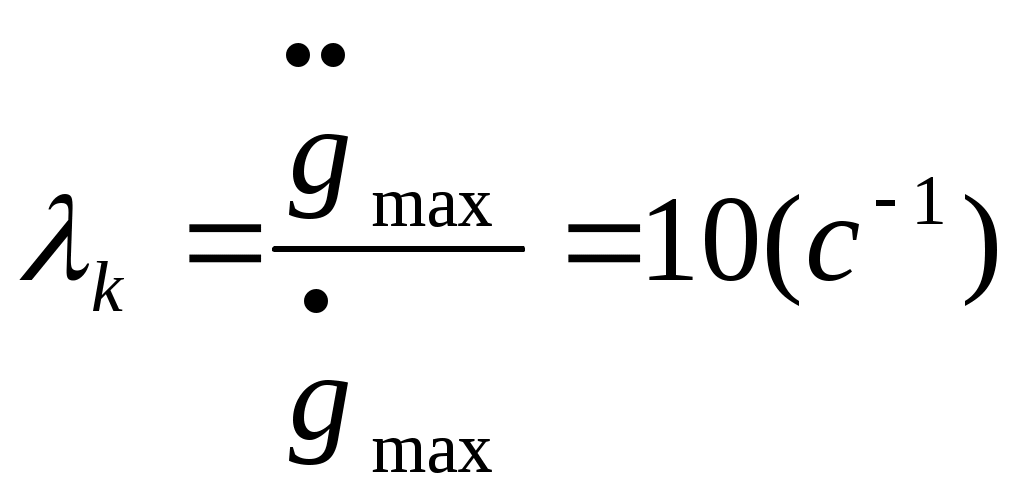
Расчет ординаты рабочей точки.
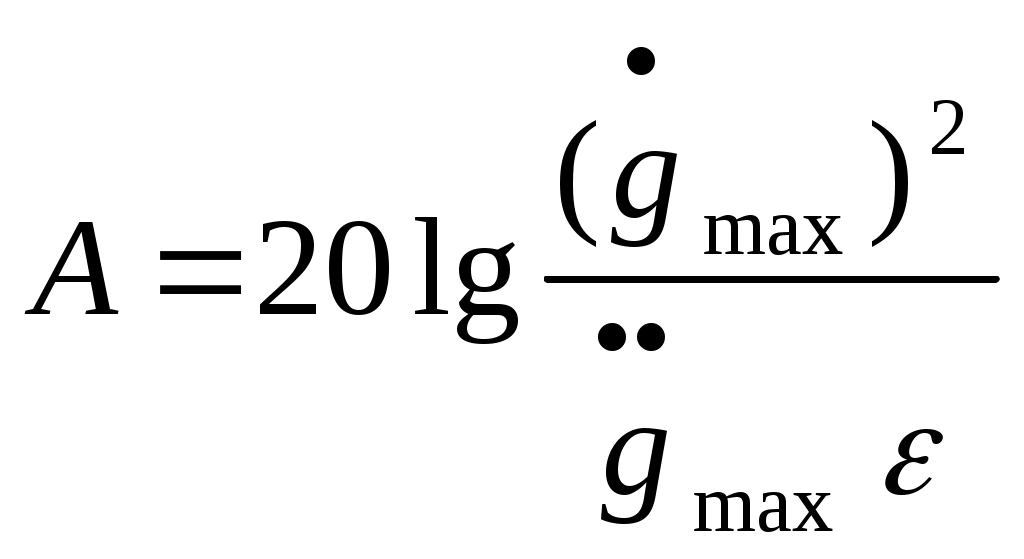 (34)
(34)
Вычислим амплитуду контрольной точки:
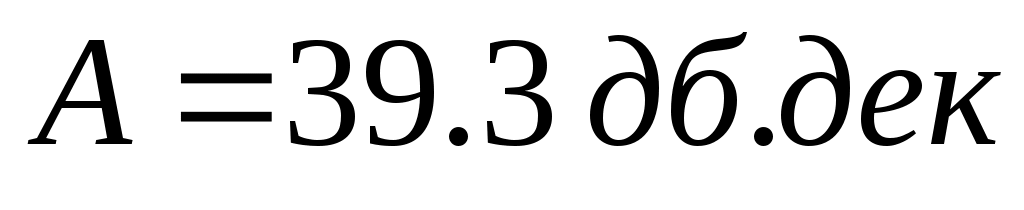
Подставим числовые значения в выражения
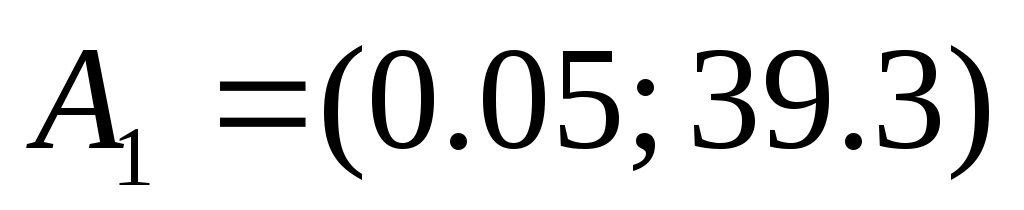 (35)
(35)
Таким образом, можно сформулировать требования к низкочастотной части желаемой ЛАЧХ системы: для того что бы входное гармоническое воздействие с ошибкой, не превышающей доп, ЛАЧХ системы должна проходить не ниже контрольной точки Ак (0,05;39,3), то есть строим запретную область. Через данную точку проводим прямую с наклоном – 20 дБ/дек с целью формирования запретной зоны, полуплоскость, находящаяся под этой прямой является запретной зоной.
Построение среднечастотной асимптоты ЖЛАЧХ начинают с выбора частоты среза. По номограмме Солодовникова (рисунок 28) и желаемому перерегулированию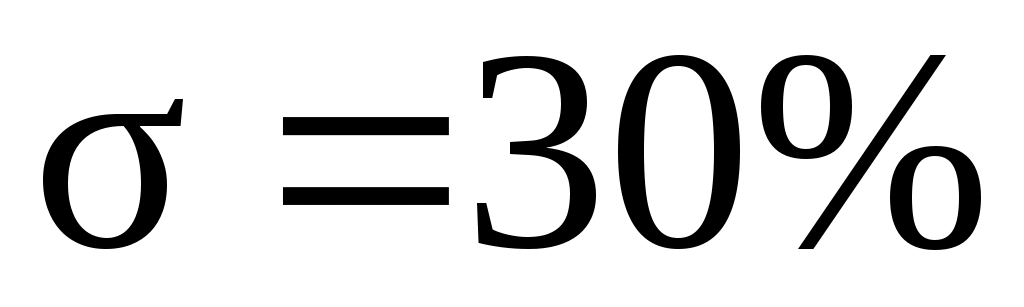 и времени регулирования (tр=186 c) определяем частоту среза
и времени регулирования (tр=186 c) определяем частоту среза
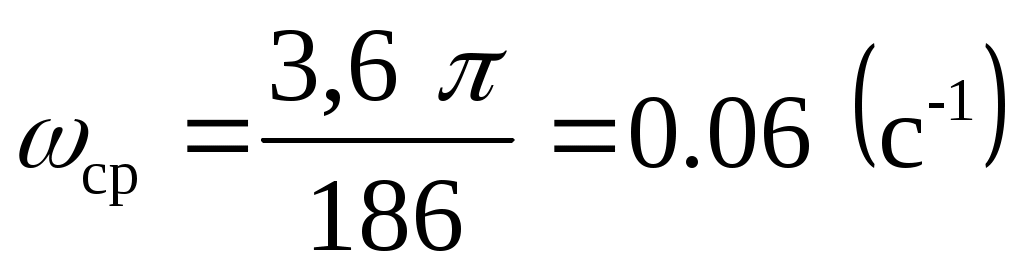 (36)
(36)
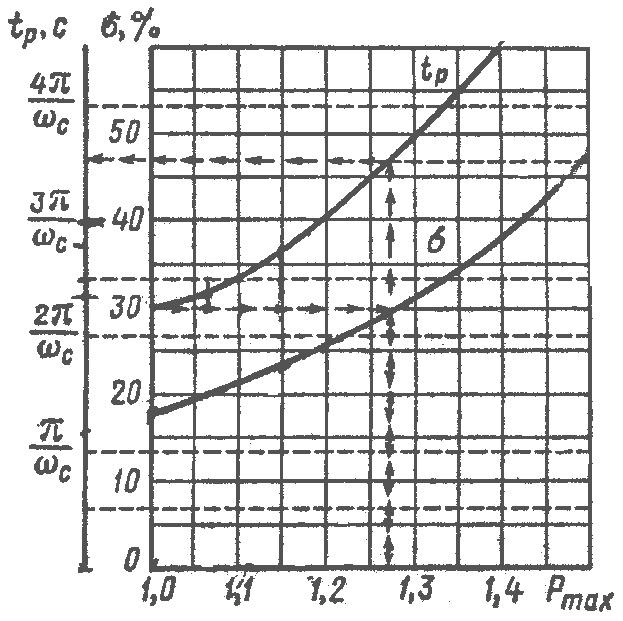
Рисунок 28 – Номограмма Солодовникова
M=1.27
Среднечастотная асимптота ЖЛАЧХ проводится через точку cр с наклоном –20 дб/дек, который обеспечивает необходимый запас по фазе.
Протяженность h среднечастотной асимптоты устанавливается исходя из необходимого запаса устойчивости. Из этих же соображений выбирается ее сопряжение с низкочастотной асимптотой.
Показатель колебательности h характеризует склонность системы к колебаниям. Чем больше М, тем меньше запас устойчивости системы.
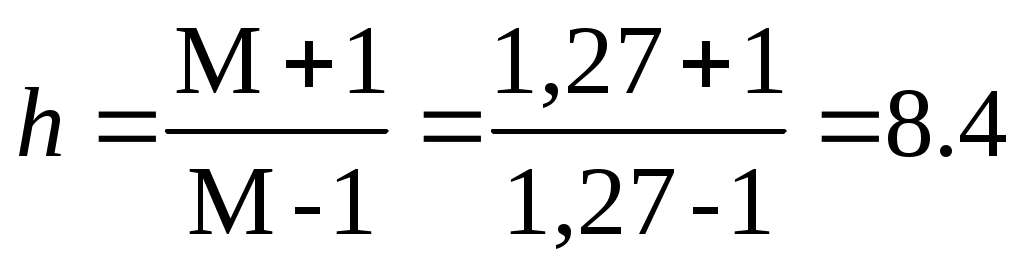
Границы среднечастотной асимптоты
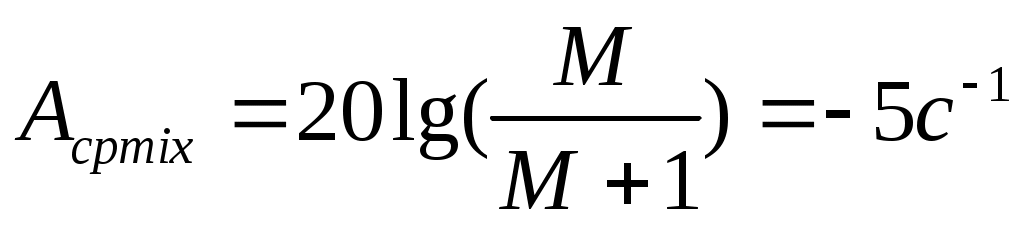 (37)
(37)
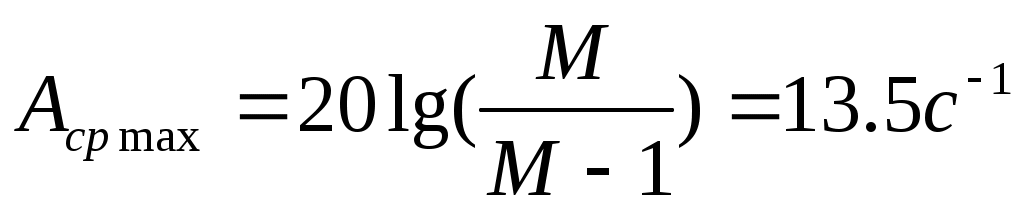
(38)
Используя полученные данные, строим желаемую характеристику, обеспечивающую необходимые показатели качества системы. Через частоту среза проводится среднечастотная асимптота с наклоном –20 дб/дек, высокочастотная часть системы мало влияет на устойчивость, поэтому ее достроим эквидистантно к высокочастотной части ЛАЧХ неизменяемой части системы.
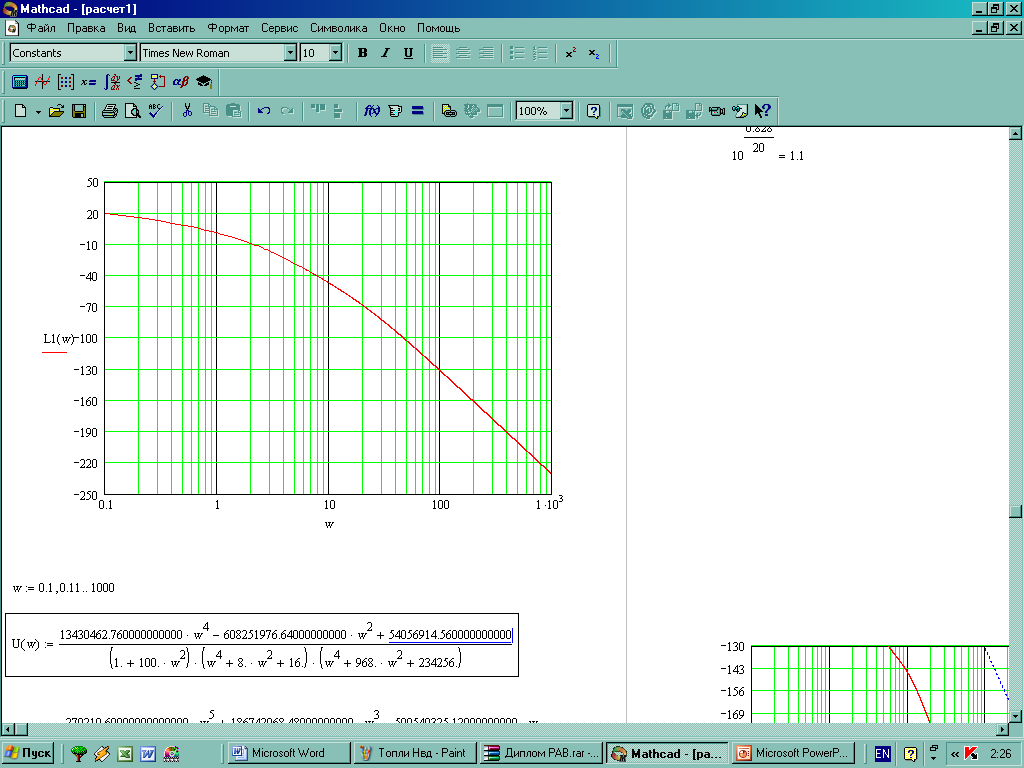
Рисунок 29 - Желаемая ЛАЧХ




5.6 Определение запасов устойчивости.
По полученной передаточной функции определяется логарифмическая фазовая характеристика (ЛФЧХ) скорректированной системы.
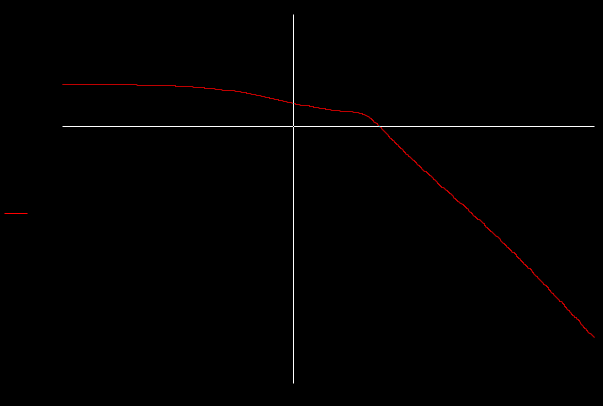
Рисунок 30 - Желаемая ЛФЧХ
Определение запасов устойчивости производится следующим образом: в точке пересечения графика ЛФЧХ с осью 180 восстанавливается перпендикуляр до пересечения с осью абсцисс. От оси абсцисс до желаемой ЛАЧХ определяется запас устойчивости по амплитуде, в нашем случае он равен 70дБ. Запас по фазе определяется по прямой, проходящей через частоту среза от оси 180 до графика ЛФЧХ. Он равен = 170, что удовлетворяет техническому заданию.
Синтез корректирующих звеньев. Коррекция динамических свойств САУ осуществляется для выполнения требований по точности, устойчивости и качеству переходных процессов.
С точки зрения требований к точности коррекция может потребоваться для увеличения порядка астатизма или коэффициента передачи системы при сохранении устойчивости и определенного качества переходного процесса.
Коррекция применяется также как средство обеспечения устойчивости, а так же повышения качества переходного процесса.
Осуществляется коррекция введением в систему корректирующих звеньев с особо подобранной передаточной функцией. Принципиально корректирующие звенья могут включаться либо последовательно с основными звеньями САУ, либо параллельно им, также существуют и комбинированные способы включения. Соответственно, по способу включения в систему корректирующие звенья делятся на последовательные и параллельные.
Логарифмические частотные характеристики представляют собой амплитудную и фазовую частотные характеристики САР, построенные в полулогарифмическом масштабе.
Логарифмической амплитудной частотной характеристикой (ЛАЧХ) системы называется кривая, соответствующая 20 десятичным логарифмам модуля частотной характеристики (АЧХ), построенная в десятичном логарифмическом масштабе частот:
где
Тогда для построения ЛАЧХ можно использовать передаточную функцию непрерывной разомкнутой системы. Данное выражение представляет собой произведение коэффициента усиления и передаточных функций элементарных динамических звеньев.
Известно, что псевдочастота практически совпадает с круговой частотой в области, где выполняется условие:
T0<2Tmin, (30)
где Tmin – минимальная постоянная времени элементов разомкнутой системы.
Так как минимальная постоянная времени, соответствующая датчика положения равна 8 с., выбранный период дискретизации – 6, то неравенство выполняется всегда (6<2.8) и во всей области работы системы можно положить



Рисунок 24 - ЛАЧХ разомкнутой системы



Рисунок 25 - ЛФЧХ разомкнутой системы
По построенным характеристикам определим запасы по фазе и амплитуде. Запас по амплитуде определяется следующим образом. Находится частота при которой ЛФЧХ первый раз пересекает прямую со значением -1800, в этой частоте проводится вертикальная прямая до пересечения с ЛАЧХ.
Расстояние от этой точки пересечения до оси составляет запас устойчивости по амплитуде в децибелах. В нашем случае запас по амплитуде 50 дб/дек.
Запас устойчивости по фазе определяется следующим образом. Определяется частота при которой ЛАЧХ пересекает ось (0 децибел). При этой частоте проводится вертикальная прямая вниз до пересечения с ЛФЧХ. Расстояние от точки пересечения до прямой -1800 составит запас по фазе в градусах. В нашем случае ЛАЧХ пересекает ось 0, следовательно, запас по фазе составляет 20,75°.
Так как время переходного процесса не соответствует требуемому, то системе требуется коррекция.
5.4 Анализ качества системы
5.3.1 Прямые оценки качества. Для наглядного отображения свойств рассматриваемой системы построим переходный процесс, воспользовавшись обратным преобразованием Лапласа от передаточной функции замкнутой системы.
По графику переходного процесса (рисунок 24) определим прямые показатели качества системы:
а) Время регулирования (время переходного процесса) - время, за которое система приходит к установившемуся значению с некоторой долей погрешности. Обычно она составляет 5% (пятипроцентная трубка). Приблизительно время регулирования составляет 186,3 (с).
tp = 186,3с
Время первого согласования t1=325.
б) Перерегулирование отражает в процентах максимальное отклонение от установившегося значения.
Максимальное значение отсутствует, тогда перерегулирование:


Рисунок 26– Переходный процесс нескорректированной системы
По характеру переходного процесса можно судить об устойчивости системы: характеристика устойчивая монотонно возрастающая.
5.3.2 Косвенные оценки качества. Косвенные оценки качества проводятся по частотным характеристикам. Наиболее часто используется амплитудно-частотная характеристика. (АЧХ) замкнутой системы.
Амплитудно-частотная функция определяется по формуле:
График АЧХ замкнутой системы приведен на рисунке 25.
Косвенные оценки качества:
- показатель колебательности, определяемый по формуле
где Amax – максимум АЧХ;
A(0) – значение амплитуды при нулевой частоте.
A(0)=0,99 рад/с
Amax=20,6
В данном случае M=21 – переходный процесс протекает с колебаниями по апериодическому закону.

Рисунок 27 – АЧХ системы
- Частота среза – частота, при которой АЧХ достигает значения, равного 1.
Частота среза косвенно характеризует быстродействие системы: чем больше часта среза, тем меньше время регулирования.
λср= 1,8 рад/с
- Резонансная частота – частота, в которой амплитудно-частотная функция достигает своего максимального значения:
λр=0,46 рад/с
- Полоса пропускания – интервал частот, в котором амплитуда АЧХ превышает уровень 0.707 Amax
0.245<ω<0.644
5.5 Построение желаемой ЛАЧХ.
Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства. Желаемая ЛАЧХ строится на основании требований к системе, отраженных в техническом задании, при этом рекомендуется, чтобы характеристика не скорректированной системы и желаемая характеристика скорректированной системы совпадали друг с другом в возможно более широком диапазоне частот. В противном случае реализация корректирующих устройств резко усложняется.
Построим желаемую ЛАЧХ исследуемой системы, используюя метод запретной области.
Рассмотрим низкочастотную часть желаемой ЛАЧХ системы.
Отметим в низкочастотной области желаемой ЛАЧХ запретную зону для обеспечения требований по ошибке при заданных скорости и ускорении входного сигнала.
Запишем некоторые данные из технического задания для нашей системы:
Максимально допустимая ошибка
Максимальна скорость изменения pH пульпы
Максимальное ускорение
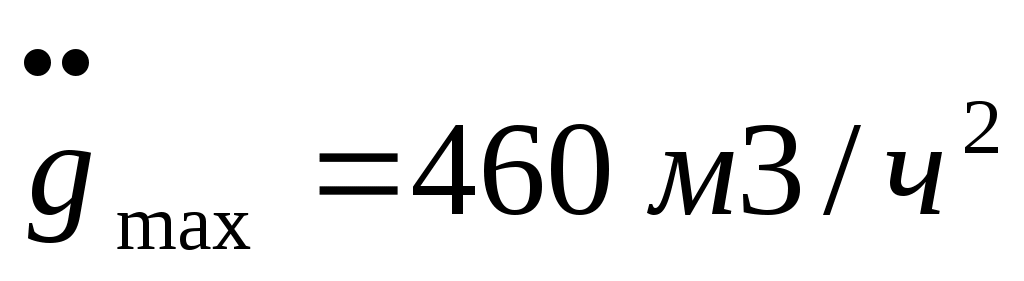
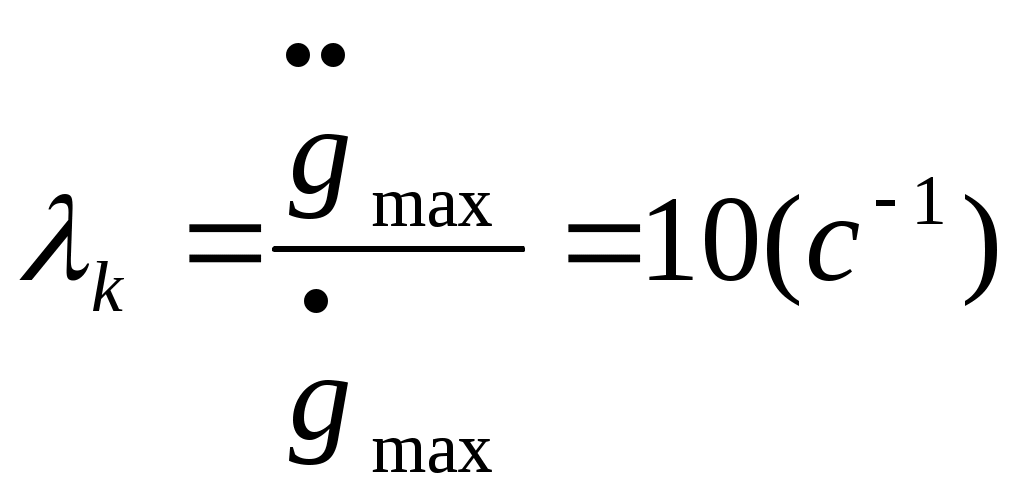
Расчет ординаты рабочей точки.
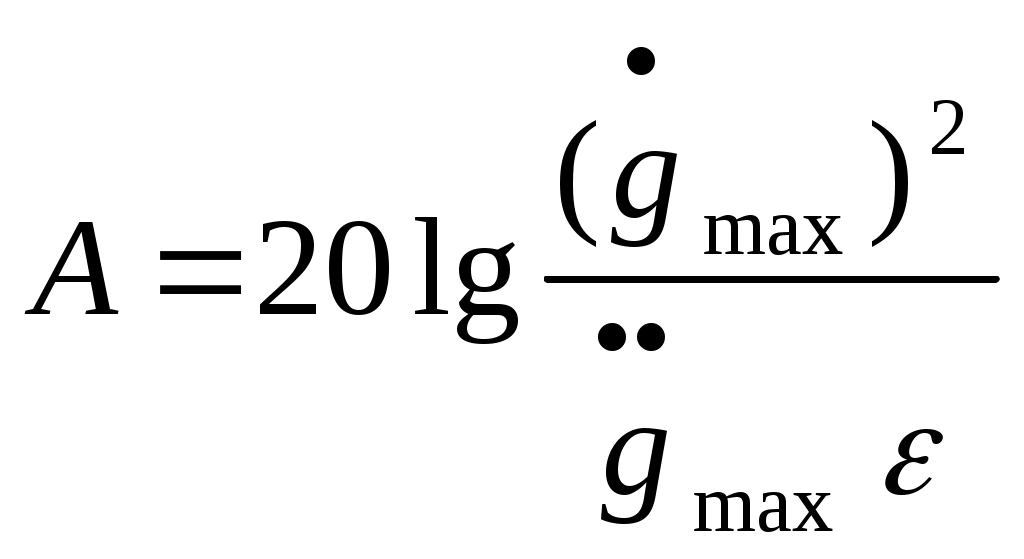 (34)
(34)Вычислим амплитуду контрольной точки:
Подставим числовые значения в выражения
Таким образом, можно сформулировать требования к низкочастотной части желаемой ЛАЧХ системы: для того что бы входное гармоническое воздействие с ошибкой, не превышающей доп, ЛАЧХ системы должна проходить не ниже контрольной точки Ак (0,05;39,3), то есть строим запретную область. Через данную точку проводим прямую с наклоном – 20 дБ/дек с целью формирования запретной зоны, полуплоскость, находящаяся под этой прямой является запретной зоной.
Построение среднечастотной асимптоты ЖЛАЧХ начинают с выбора частоты среза. По номограмме Солодовникова (рисунок 28) и желаемому перерегулированию

Рисунок 28 – Номограмма Солодовникова
M=1.27
Среднечастотная асимптота ЖЛАЧХ проводится через точку cр с наклоном –20 дб/дек, который обеспечивает необходимый запас по фазе.
Протяженность h среднечастотной асимптоты устанавливается исходя из необходимого запаса устойчивости. Из этих же соображений выбирается ее сопряжение с низкочастотной асимптотой.
Показатель колебательности h характеризует склонность системы к колебаниям. Чем больше М, тем меньше запас устойчивости системы.
Границы среднечастотной асимптоты
(38)
Используя полученные данные, строим желаемую характеристику, обеспечивающую необходимые показатели качества системы. Через частоту среза проводится среднечастотная асимптота с наклоном –20 дб/дек, высокочастотная часть системы мало влияет на устойчивость, поэтому ее достроим эквидистантно к высокочастотной части ЛАЧХ неизменяемой части системы.

Рисунок 29 - Желаемая ЛАЧХ





5.6 Определение запасов устойчивости.
По полученной передаточной функции определяется логарифмическая фазовая характеристика (ЛФЧХ) скорректированной системы.
Рисунок 30 - Желаемая ЛФЧХ
Определение запасов устойчивости производится следующим образом: в точке пересечения графика ЛФЧХ с осью 180 восстанавливается перпендикуляр до пересечения с осью абсцисс. От оси абсцисс до желаемой ЛАЧХ определяется запас устойчивости по амплитуде, в нашем случае он равен 70дБ. Запас по фазе определяется по прямой, проходящей через частоту среза от оси 180 до графика ЛФЧХ. Он равен = 170, что удовлетворяет техническому заданию.
Синтез корректирующих звеньев. Коррекция динамических свойств САУ осуществляется для выполнения требований по точности, устойчивости и качеству переходных процессов.
С точки зрения требований к точности коррекция может потребоваться для увеличения порядка астатизма или коэффициента передачи системы при сохранении устойчивости и определенного качества переходного процесса.
Коррекция применяется также как средство обеспечения устойчивости, а так же повышения качества переходного процесса.
Осуществляется коррекция введением в систему корректирующих звеньев с особо подобранной передаточной функцией. Принципиально корректирующие звенья могут включаться либо последовательно с основными звеньями САУ, либо параллельно им, также существуют и комбинированные способы включения. Соответственно, по способу включения в систему корректирующие звенья делятся на последовательные и параллельные.